資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++ 中的二叉搜尋樹 - 刪除操作
二叉搜尋樹 (BST) 是一種特殊的樹，它遵循以下規則：
左子節點的值始終小於父節點
右子節點的值始終大於父節點。
所有節點都各自構成一個二叉搜尋樹。
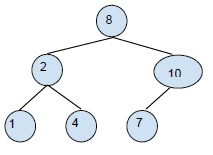
二叉搜尋樹 (BST) 示例：
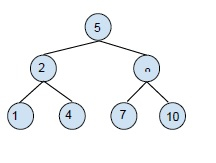
建立二叉搜尋樹是為了降低搜尋、查詢最小值和最大值等操作的複雜度。
二叉搜尋樹 (BST) 的刪除操作
刪除操作是從樹中刪除指定的節點。在刪除節點時，有三種可能性：
從樹中刪除葉子節點：最簡單的刪除是從二叉搜尋樹中刪除葉子節點。刪除葉子節點只會影響葉子節點本身。例如：
刪除葉子節點 7 得到：
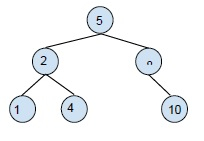
刪除只有一個子節點的節點：對於此刪除操作，需要用要刪除的節點的子節點替換該節點，然後刪除該節點。例如：
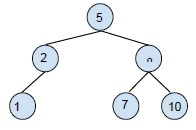
從 BST 中刪除 2
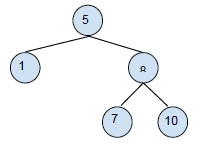
刪除有兩個子節點的節點：此處要刪除的節點有兩個子節點。因此，我們將使用樹的中序遍歷形式，在這裡我們將刪除該元素並選擇其中序鄰接節點來代替它，然後重建其餘部分。例如：
從 BST 中刪除 5 將返回以下樹。
示例
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inordertraversal(struct node *root){
if (root != NULL){
inordertraversal(root->left);
printf("%d ", root->key);
inordertraversal(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
struct node * minValueNode(struct node* node){
struct node* current = node;
while (current && current->left != NULL)
current = current->left;
return current;
}
struct node* deleteNode(struct node* root, int key){
if (root == NULL) return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else{
if (root->left == NULL){
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL){
struct node *temp = root->left;
free(root);
return temp;
}
struct node* temp = minValueNode(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
return root;
}
int main(){
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inordertraversal(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
return 0;
}輸出
Inorder traversal of the given tree 20 30 40 50 60 70 80 Delete 20 Inorder traversal of the modified tree 30 40 50 60 70 80 Delete 30 Inorder traversal of the modified tree 40 50 60 70 80 Delete 50 Inorder traversal of the modified tree 40 60 70 80
更新於：2020年1月3日
4K+ 次瀏覽
廣告