最小生成樹與最短路徑的區別

介紹

最小生成樹和最短路徑在圖論領域設計網路方面起著至關重要的作用。雖然它們作為基本概念具有相似之處，但其目的卻大相徑庭。在本文中，我們將深入探討圖中這兩個有趣的元素，並重點介紹它們的區別。最小生成樹 (MST) 的目標是在所有頂點之間建立最小成本的連線，並且沒有迴圈，而最短路徑的目標是根據距離或權重累加來識別特定節點之間的最佳路徑。

最小生成樹與最短路徑的區別

圖論提供了各種工具，可以有效地分析網路中的連線和路徑。雖然最小生成樹和最短路徑由於其對最佳化的關注而看起來相似，但它們在不同的場景中具有不同的用途。讓我們來看一個簡單的示例生成樹圖，

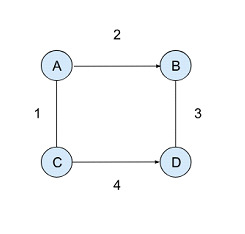
最小生成樹

最小生成樹定義為一個子圖，它包含無向加權圖的所有頂點，並且總邊權重最小。構建 MST 的主要目標是在所有節點之間建立連線，同時最小化它們之間的總成本或距離。

為了建立 MST，可以使用克魯斯卡爾演算法或普里姆演算法等各種演算法。這些演算法遍歷每個頂點，直到使用具有最小可能權重的邊連線每個節點，從而形成一個沒有迴圈的樹狀結構。MST 的一個突出的現實生活應用在於通訊網路（如電信或電力分配系統）；它有助於以最低成本建立有效的連線，透過消除可能導致資源和維護方面額外費用的不必要連結。

例如，讓我們考慮一個簡單的場景，我們旨在在一個城市中建立各個建築物之間的電力連線。每個建築物都由圖中的一個節點表示，連線它們需要鋪設電纜。為了最小化成本，我們使用克魯斯卡爾演算法或普里姆演算法來識別最小生成樹，它將代表連線所有建築物最有效的網路設計，同時最大限度地減少電纜的使用。

最短路徑

與專注於有效連線所有頂點同時最小化總權重的 MST 不同，最短路徑演算法根據長度或時間持續時間等指標識別兩個特定頂點之間的最優路徑。最短路徑為我們提供了詳細的導航說明，以便透過多箇中間節點（如果需要）從 A 點到達 B 點。迪傑斯特拉演算法是幾種其他技術中的一個經典示例，它實際上反覆探索不同的潛在路徑，直到成功確定從起點到達特定目的地的最低累積成本或權重的路徑。

最短路徑的應用範圍涵蓋了各個領域，包括交通系統規劃、為計算機網路設計的路由協議、確定最快路線的 GPS 導航應用程式、最佳化貨物交付最有效路徑的供應鏈最佳化解決方案，甚至社會網路分析測量分離度。

例如，假設我們正在使用手機上的 GPS 導航來查詢從我們當前位置（節點 A）到所需目的地（節點 B）的最快速路線。此處使用的演算法可能是迪傑斯特拉演算法或貝爾曼-福特演算法，它們根據道路長度或平均速度等因素計算最短路徑。這些演算法使我們能夠確定到達目的地的最快方式，同時考慮沿途的任何中間停靠點或繞行。

最小生成樹與最短路徑的區別

基本引數

最小生成樹

最短路徑

定義

一棵包含所有頂點並最小化總權重的樹。

具有最低累積權重或距離的路徑。

主要目標

以最小的總權重將所有節點連線在一起。

它找到特定路線之間最有效的路線。

關鍵屬性

它不包含任何迴圈。

有向邊或無向邊

演算法示例

一些例子是克魯斯卡爾演算法和普里姆演算法。

一些例子是迪傑斯特拉演算法和貝爾曼-福特演算法。

優點

它被廣泛用於網路設計（例如鋪設電纜），也用於無監督學習中的資料合併。

最短路徑可以選擇兩點之間的連線，並且它還有助於人們以最短距離導航到最終位置。

缺點

當網路設計很大時，它變得過於繁瑣。

它找到了最短路徑，但這可能不是唯一的路徑。

結論

總而言之，儘管最小生成樹和最短路徑都涉及遍歷圖並在網路中識別最佳連線，但它們的目標在客觀性和目的方面存在顯著差異。雖然 MST 提供了一種經濟的方式來實現整個圖的組成元素之間的連線，但最短路徑強調在網路中遍歷特定道路時的效率——這使我們能夠深入瞭解現實世界中旅行距離至關重要的場景。

更新於：2023年8月25日

1K+ 次瀏覽

啟動您的職業生涯

完成課程獲得認證

開始學習
廣告