資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究最小生成樹演算法
如果一個生成樹的權重小於或等於加權、連通、無向圖 $G$ 的所有可能生成樹的權重，則稱其為最小生成樹 (MST)。生成樹的權重是分配給生成樹中每條邊的所有權重的總和。以下是兩種最流行的查詢最小生成樹 (MST) 的演算法。
克魯斯卡爾演算法
克魯斯卡爾演算法是一種貪心演算法，用於查詢連通加權圖的最小生成樹。它找到該圖的一棵樹，其中包含每個頂點，並且樹中所有邊的總權重小於或等於所有可能的生成樹。
演算法
步驟 1 - 根據邊的權重，將給定圖 G (V,E) 的所有邊按非遞減順序排列。
步驟 2 - 從圖中選擇權重最小的邊，並檢查它是否與迄今為止形成的生成樹形成環。
步驟 3 - 如果沒有環，則將此邊包含到生成樹中，否則丟棄它。
步驟 4 - 重複步驟 2 和步驟 3，直到生成樹中剩下 (V-1) 條邊。
問題
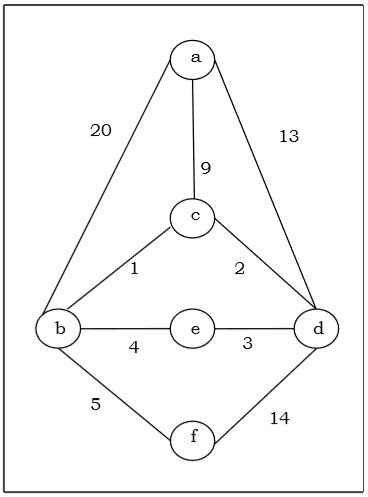
假設我們想使用克魯斯卡爾演算法為以下圖 G 找到最小生成樹。
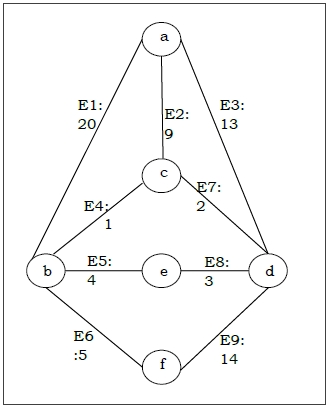
解決方案
從上圖我們構造以下表格 -
| 邊號 | 頂點對 | 邊權重 |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E4 | (b, c) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
現在我們將根據邊權重對錶格進行升序排列 -
| 邊號 | 頂點對 | 邊權重 |
|---|---|---|
| E4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
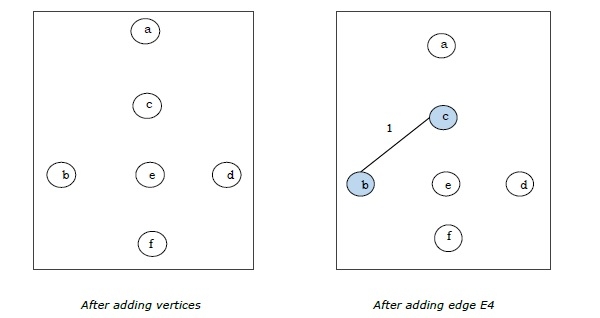
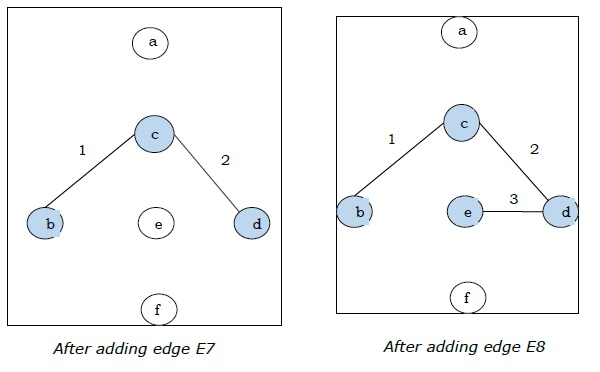
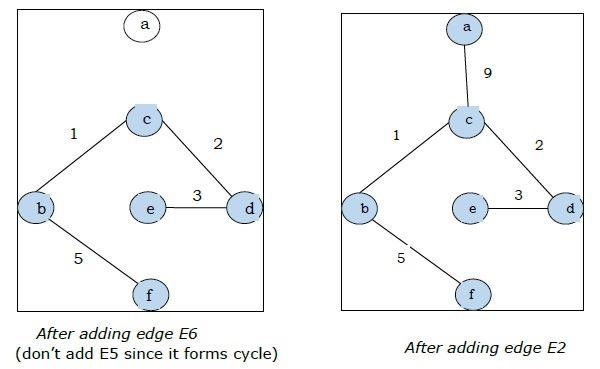
由於我們在上圖中得到了所有 5 條邊，因此我們停止演算法，這就是最小生成樹，其總權重為 (1 + 2 + 3 + 5 + 9) = 20。
普里姆演算法
普里姆演算法由數學家沃伊捷赫·亞爾尼克和羅伯特·C·普里姆於 1930 年發現，是一種貪心演算法，用於查詢連通加權圖的最小生成樹。它找到該圖的一棵樹，其中包含每個頂點，並且樹中所有邊的總權重小於或等於所有可能的生成樹。普里姆演算法在密集圖上速度更快。
演算法
用從圖中隨機選擇的單個頂點初始化最小生成樹。
重複步驟 3 和 4，直到所有頂點都包含在樹中。
選擇連線樹與尚未在樹中的頂點的邊，以便邊的權重最小，並且邊的包含不會形成環。
將選定的邊及其連線到的頂點新增到樹中。
問題
假設我們想使用普里姆演算法為以下圖 G 找到最小生成樹。
解決方案
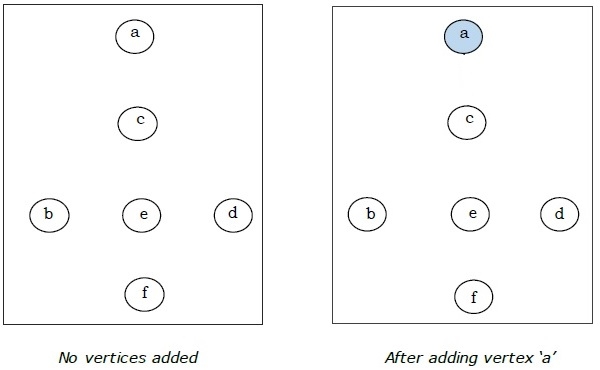
這裡我們從頂點“a”開始並繼續。
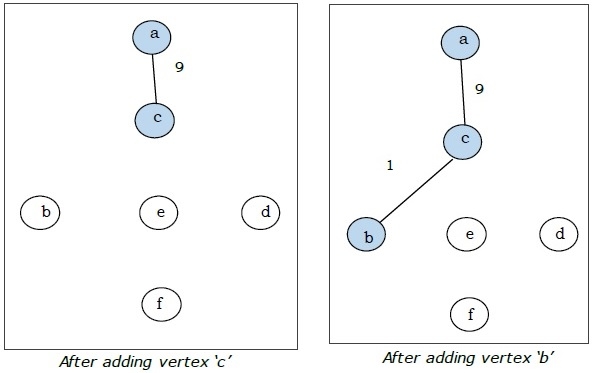
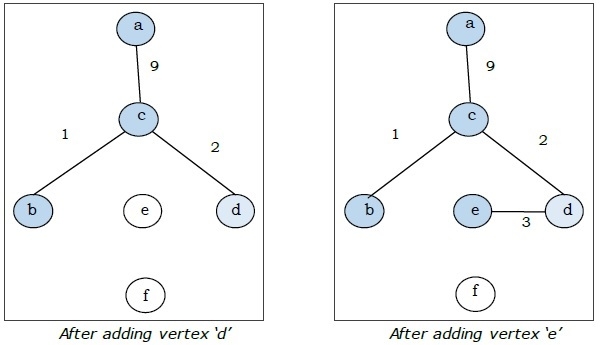
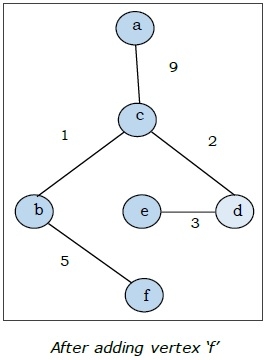
這是最小生成樹，其總權重為 (1 + 2 + 3 + 5 + 9) = 20。
5K+ 瀏覽量
