資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究資料結構中的最小生成樹
**生成樹**是無向圖的一個子集，它透過最少的邊將所有頂點連線起來。
如果圖中所有頂點都連線，則至少存在一個生成樹。在一個圖中，可能存在多個生成樹。
最小生成樹
**最小生成樹 (MST)** 是連線加權無向圖中所有頂點的具有最小可能總邊權重的邊的子集。為了匯出 MST，可以使用 Prim 演算法或 Kruskal 演算法。因此，我們將在本章中討論 Prim 演算法。
正如我們所討論的，一個圖可能有多個生成樹。如果有 **n** 個頂點，則生成樹應該有 **n - 1** 條邊。在這種情況下，如果圖的每條邊都與權重相關聯，並且存在多個生成樹，我們需要找到圖的最小生成樹。
此外，如果存在任何重複的加權邊，則圖可能具有多個最小生成樹。
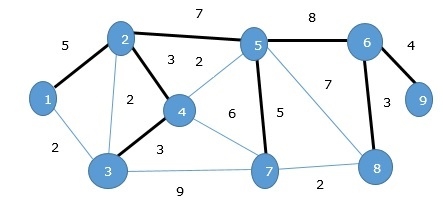
在上圖中，我們展示了一個生成樹，儘管它不是最小生成樹。此生成樹的成本為 (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38。
更新於: 2019年8月27日
16K+ 瀏覽量
廣告