圓柱體

---

引言

繞平行於其自身的固定直線旋轉線段所得到的圓柱體稱為旋轉圓柱體。在我們的日常生活中，我們熟悉許多圓柱形物體。傳統上，圓柱體或圓柱形結構的定義包括一個具有稜柱形形狀和圓形底部的三維實體，例如鉛筆、壓路機和管道是一些基本的圓柱體示例。

這是最基本的曲線幾何形狀之一。這種傳統觀點在解決簡單的幾何問題時仍然有用。然而，從複雜的數學角度來看，圓柱面被視為無限彎曲的曲面。如今，許多現代幾何和拓撲領域都遵循這一概念。在本文中，我們將討論與圓柱形結構相關的特性、變體和公式。

今天我們將討論圓柱體的屬性、形狀中使用的引數，並處理一些問題。

圓柱體

它由平行的圓盤組成；我們可以說許多圓盤構成一個圓柱體。如果我們連線所有圓盤的中心，連線軸的線段就是圓柱體的高度。

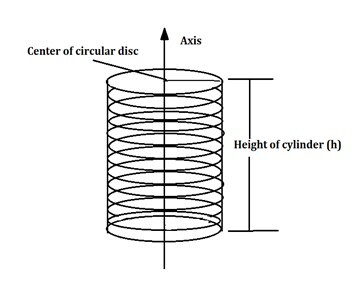
• 從頂部看，圓柱體看起來像一個圓。

• 圓柱體的正面檢視看起來像一個矩形。它具有曲線，不像立方體和長方體那樣是直線。

圓柱體的型別

• 橢圓柱體 - 橢圓柱體結構是一個具有橢圓形底部的圓柱體。

• 直圓柱體 - 透過繞其一邊作為軸旋轉矩形，建立了一個稱為直圓柱體的物體。如果軸（矩形的一邊）垂直於半徑 (r)，則該圓柱體稱為直圓柱體。圓柱體的高度 (h) 是其頂部和底部的圓形面之間的距離，這兩個圓形面彼此平行。

• 斜圓柱體 - 斜圓柱體是指圓形面側向而不是彼此疊加，並且軸與底面形成非直角的圓柱體。

• 空心圓柱體 - 空心圓柱體是一種圓柱形結構，其內外表面直徑存在差異，內部為空心。由於內外徑可變，因此它們可以具有不同的內外側表面積。

圓柱體的公式

在三維幾何中，圓柱體佔據的整個空間稱為其面積。圓柱體的面積包括兩個圓形底部的總表面積加上側表面積。兩個圓形底部之間有一個彎曲的或側表面。當彎曲的表面開啟時，表示一個矩形。高度、半徑、軸、邊和底是用於計算圓柱體面積的許多變數。圓柱體的半徑等於其兩個圓形邊之間的距離。兩個圓形邊之間的垂直距離稱為圓柱體的高度，其半徑可以寫成 (r)。圓柱體的高度指定為 (h)

圓柱形結構的表面積可分為兩類。

• 曲面面積 (CSA)

• 總表面積 (TSA)

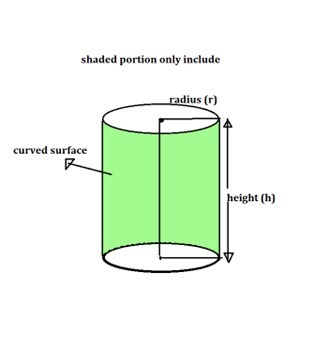
曲面面積或側表面積

側表面積是曲面面積的另一個名稱。曲面的面積是圓柱形結構的面積，不包括其圓形底部的面積。

一般情況下，面積使用平方釐米、平方米等平方單位來測量。

如果開啟圓柱體的曲面面積，可以看到一個矩形。

曲面面積上的兩個圓形邊緣的大小可能與圓的直徑相符。

圓的周長可以使用公式 2r 計算。

因此，矩形的長度（開啟曲面後）為 2r，其寬度為 (h)。因此，曲面的面積為 2Πrh。

所以，公式如下所示：

$$\mathrm{圓柱體的曲面面積 = 2Πrh 平方單位.}$$

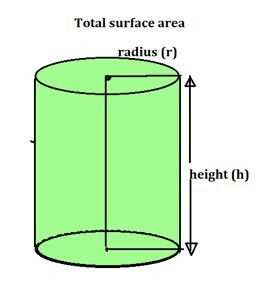
總表面積

圓柱體的總表面積是兩個圓的面積和彎曲或側表面的面積之和，其公式如下：

總表面積 = 兩個圓的面積 + 曲面面積

$$\mathrm{=2×Πr^2+2Πrh }$$

$$\mathrm{ =2Πr(r+h) 平方單位}$$

體積

每個實體或三維形狀都具有佔據一定空間的體積。圓柱體在任何三維平面中佔據的區域就是它的體積。圓柱體的容量表示其內部可能容納多少水。

$$\mathrm{圓柱體的體積 = Πr^2 h 立方單位}$$

例題

1)如果圓柱體的高度為 12 釐米，圓柱體的體積為 8478 立方厘米，那麼圓柱體的半徑是多少？

答案

已知，圓柱體的高度 (h) = 12 釐米

圓柱體的體積 (v) = 8478 立方厘米

我們知道，

圓柱體的體積 (v) = Πr² h

$$\mathrm{8478 = 3.14×r^2×12}$$

$$\mathrm{8478 = 37.68×r^2}$$

$$\mathrm{225 = r^2}$$

因此，r = 15 釐米

所以圓柱體的半徑是 15 釐米。

2)如果水箱的直徑和高度分別為 30 釐米和 40 釐米，那麼圓柱形水箱的體積是多少？

答案

已知，圓柱形水箱的高度 (h) = 40 釐米

圓柱形水箱的直徑 (d) = 30 釐米

所以，圓柱形水箱的半徑 (r) = 30/2 = 15 釐米

我們知道，

圓柱體的體積 = Πr² h

$$\mathrm{= 3.14×15×15×40}$$

$$\mathrm{= 28260 立方厘米}$$

3) 半徑和高度分別為 7 釐米和 20 釐米的圓柱體的總表面積是多少？

答案

已知：

圓柱體的半徑 (r) = 7 釐米

圓柱體的高度 (h) = 20 釐米

我們知道，

圓柱體的總表面積 = 2Πr(r+h)

$$\mathrm{= 2×3.14×7×(20 +7)}$$

$$\mathrm{ = 1,186.92 平方釐米}$$

所以，圓柱體的表面積是 1,186.92 平方釐米。

結論

圓柱形結構具有零個頂點、兩個邊、一個曲面和兩個底面。它有兩個底面，就像稜柱一樣。它們的形狀可分為四類：空心圓柱形結構、橢圓柱體、直圓柱體和圓柱形結構。圓柱形結構有兩個平行的底面，兩個底面之間的距離稱為其高度。

• 圓柱體的曲面面積 = 2Πrh 平方單位。

• 圓柱體的總表面積 = 兩個圓的面積 + 曲面面積

  $$\mathrm{= 2×Πr^2+2Πrh}$$

  $$\mathrm{= 2Πr(r+h) 平方單位}$$

• 圓柱體的體積 = Πr² h 立方單位

常見問題

1. 圓柱體有多少個面？

圓柱體有兩個平坦的圓形側面和一個曲面。因此，它總共有三個面。

2. 圓柱體有頂點嗎？

構成圓柱體的兩個平行的圓形側面具有相同的形狀。但是，由於其曲率，它沒有任何頂點。

3. 還有哪些其他型別的圓柱體？

直圓柱體、斜圓柱體、橢圓柱體和空心圓柱體是四種不同型別的圓柱體。

4. 什麼使圓柱體成為一個三維形狀？

圓柱體是一個三維形狀，兩端有兩個平行的圓形側面。一個曲面。沒有頂點或邊。