資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++二叉樹中非葉子節點的計數
給定一個二叉樹，任務是計算二叉樹中非葉子節點的數量。
二叉樹是一種用於資料儲存的特殊資料結構。二叉樹有一個特殊條件，即每個節點最多可以有兩個子節點。二叉樹結合了有序陣列和連結串列的優點，搜尋速度像排序陣列一樣快，插入或刪除操作像連結串列一樣快。非葉子節點也稱為父節點，因為它們具有多於0個子節點且少於2個子節點。
二叉樹的結構如下所示：
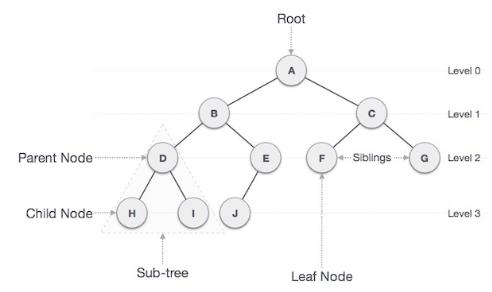
例如
輸入：
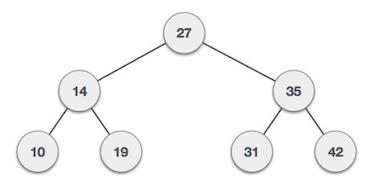
輸出：非葉子節點數量為：3
解釋：在給定的樹中，27、14和35是非葉子節點，因為它們具有多於0個子節點且少於2個子節點。
下面程式中使用的演算法如下：
建立二叉樹結構，包含指向左節點的指標、指向右節點的指標以及儲存在節點中的資料部分。
建立一個函式，每當呼叫此函式時都會插入一個節點。為此，將資料插入新節點，並將新節點的左右指標設定為NULL，然後返回該節點。
建立一個遞迴函式，用於計算二叉樹中非葉子節點的數量。
- 檢查根節點是否為NULL，或者根節點的左子節點和右子節點是否為NULL，如果是，則返回0。
- 返回1 + 對此函式的遞迴呼叫（使用左指標）+ 對此函式的遞迴呼叫（使用右指標）。
列印計數。
示例
#include <iostream>
using namespace std;
// Node's structure
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// To define the new node
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
// Count the non leaf nodes.
int nonleaf(struct Node* root){
if (root == NULL || (root->left == NULL && root->right == NULL)){
return 0;
}
return 1 + nonleaf(root->left) + nonleaf(root->right);
}
// Main function
int main(){
struct Node* root = newNode(10);
root->left = newNode(21);
root->right = newNode(33);
root->left->left = newNode(48);
root->left->right = newNode(51);
cout << nonleaf(root);
return 0;
}輸出
如果執行以上程式碼，將生成以下輸出：
count of non-leaf nodes is: 2
更新於：2020年5月15日
2K+ 次瀏覽
廣告