連續整數

---

介紹

連續整數是指按照特定順序或次序依次排列的整數。自然數、整數、有理數和無理數、實數和整數是一些數字型別。整數是包含所有正整數、負整數和零的集合。“整數”是一個拉丁詞，意為完整或全部。這意味著分數或小數不包含在整數中。

• 例如，1、−5、4、9、−6。我們可以對整數進行基本的算術運算，即加法、減法、乘法和除法。連續整數是指按照特定模式或順序依次排列的數字。連續整數之間的差值始終是常數。這些整數按升序排列。這個概念用於構建文字題。

整數

• 定義為包含所有整數、負數和零的集合。

• 正數、負數和零構成一組稱為

• 它們用 Z 表示。

• 這些數字是整數，它們沒有分數或小數部分。

• −5、0、8、−6、96、32 是一些整數的例子。

• 整數在數軸上表示。

• 正數標記在數軸的右側。而負數標記在數軸的左側。

• 零既不是正數也不是負數，因此它標記在數軸的中間。

• 這個點稱為數軸的原點。

• 下圖表示數軸上的整數。

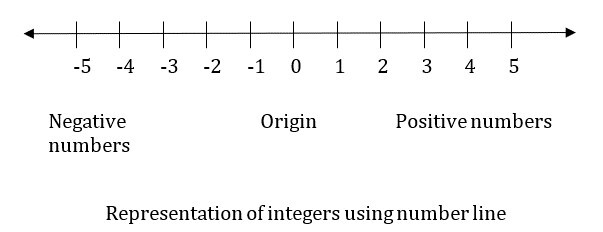
• 這些運算可以透過兩種方式執行，要麼使用代數規則，要麼使用數軸。

連續整數

• 連續整數是指按照特定順序或模式依次排列的數字。

• 每個連續整數之間的差值是常數，即固定值。

• 例如，自然數集 1、2、3、4、5、6、……，在這裡我們可以看到每個項之間的差值都是 1。

• 如果 n 是任何數字，則數字序列可以表示為 n+1、n+2、……、n+m，其中 m 表示序列中的最後一個數字。

• 這些數字按升序排列。

• 連續整數的一般公式為 n+1。

連續正數和負數

• 要找到連續整數的序列，第一個整數必須為正數或大於零才能獲得一系列正數。

• 由於連續整數按升序排列，因此其他數字預設情況下將為正數。

• 此術語用於計數。

• 而要找到連續負整數的序列，第一個整數必須為負數或小於零才能獲得一系列負數。

• 由於連續整數按升序排列，因此其他數字預設情況下將為負數。

連續偶數和奇數整數

連續偶數整數

• 偶數是 2 的倍數。連續偶數整數是一組偶數整數。

• 連續偶數整數之間的差值是 2。

• 假設 𝑧 是任何整數，則連續偶數整數可以寫成 𝑧、𝑧 + 2、𝑧 + 4 等。

• 連續偶數整數的一般公式為 2n，其中 n 是任何整數。

連續奇數整數

• 奇數不是 2 的倍數。連續奇數整數是一組奇數整數。

• 連續奇數整數之間的差值是 2。

• 假設 z 是任何整數，則連續奇數整數可以寫成 𝑧、𝑧 + 2、𝑧 + 4 等。

• 連續奇數整數的一般公式為 2n+1，其中 n 是任何整數。

兩個連續整數的乘積（始終非負）

• 假設 m 和 n 是任何兩個連續整數，並且 m 和 n 的乘積表示為

$$\mathrm{Product\:=\:m\times\:n}$$

• 例如，$\mathrm{2\times\:1\:=\:1}$

$\mathrm{--4\times\:-3\:=\:12}$

$\mathrm{-9\times\:-8\:=\:72}$

• 從以上示例可以看出，連續數字的乘積是 2 的倍數。

• 因此，連續數字的乘積是 2 的倍數，即偶數

• 此外，兩個整數的乘積為正。

解題示例

1) 在序列 3、6、9、…、15、18、21、24 中找到缺失的數字？

答案 - 序列中連續數字之間的差值是 3。缺失數字的前一個數字是 9，後一個數字是 15。

缺失的數字 = 前一個數字 + 差值 = 9 + 3 = 12。

2) 如果三個連續數字的和為 51，則求出這三個連續數字？

答案 - 假設三個連續數字為 𝑛、𝑛 + 1 和 𝑛 + 2。

三個連續數字的和為 51

$$\mathrm{n\:+\:n\:+\:1\:+\:n\:2\:=\:51}$$

$$\mathrm{3n\:+\:3\:=\:51}$$

$$\mathrm{3n\:-\:51\:-\:3}$$

$$\mathrm{3n\:=\:48}$$

$$\mathrm{n\:=\:\frac{48}{3}}$$

$$\mathrm{n\:=\:16}$$

第一個連續數字是 16。

第二個數字 $\mathrm{=\:n\:+\:1\:=\:16\:+\:1\:=\:17}$

第三個數字 $\mathrm{=\:n\:+\:2\:=\:16\:+\:2\:=\:18}$

三個連續整數是 16、17 和 18。

3) 如果四個連續奇數整數的和為 112，則求出連續整數？

答案 - 兩個連續奇數之間的差值為 2。假設第一個整數為 𝑛，第二個、第三個和第四個奇數整數將分別為 $\mathrm{n\:+\:2,n\:+\:4\&\:n\:+\:6}$。

已知四個連續整數的和為 112。

$$\mathrm{n\:+\:n\:+\:2\:+\:n\:+\:4\:+\:n\:+\:6\:=\:112}$$

$$\mathrm{4n\:+\:12\:=\:112}$$

$$\mathrm{4n\:=\:112\:-\:12}$$

$$\mathrm{4n\:=\:100}$$

$$\mathrm{n\:=\:\frac{100}{4}}$$

$$\mathrm{n\:=\:25}$$

其他整數將為

$$\mathrm{n\:+\:2\:=\:25\:+\:2\:=\:27}$$

$$\mathrm{n\:+\:4\:=\:25\:+\:4\:=\:29}$$

$$\mathrm{n\:+\:6\:=\:25\:+\:6\:=\:31}$$

四個連續奇數整數是 25、27、29 和 31。

結論

• 本教程簡要介紹了連續整數的主題。

• 在本教程中，我們學習了整數、連續整數和兩個整數的乘積，並提供瞭解題示例。

• 整數是正數、負數和零的集合。

• 它們是整數，沒有分數或小數部分。

• 連續整數按照特定順序或次序依次排列。

• 此外，我們還討論了連續正數和負數整數以及連續偶數和奇數整數。

• 兩個連續奇數和偶數整數之間的差值是 2。

常見問題解答

1. 判斷以下陳述是真還是假，兩個連續自然數的乘積始終為偶數？

正確

2. 什麼是非連續整數？

它是一組整數，其中整數不是按順序排列的。例如，2、5、10、21

3. 偶數個整數的乘積是否為正？

是。偶數個整數的乘積為正，奇數個整數的乘積為負。

4. 整數的加法單位是什麼？

加法單位性質指出，當我們將零加到任何數字時，它會給出原始數字作為答案。零是整數的加法單位。

5. 連續數字的和是多少？

連續數字的和可以使用以下公式計算

$$\mathrm{\frac{n}{2}\times\:(第一個數字\:+\:最後一個數字)}$$