資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學架空兩相交流輸電系統中所需的導體材料
兩相交流輸電系統
當輸電系統由兩根線路導線組成，用於將交流電能從發電站傳輸到變電站進行分配時，稱為兩相交流輸電系統。
根據所用導體的數量，兩相交流輸電系統分為兩種型別，即：
- 兩相三線交流系統
- 兩相四線交流系統
兩相三線交流系統中所需的導體材料
考慮圖 1 所示的兩相三線交流系統。
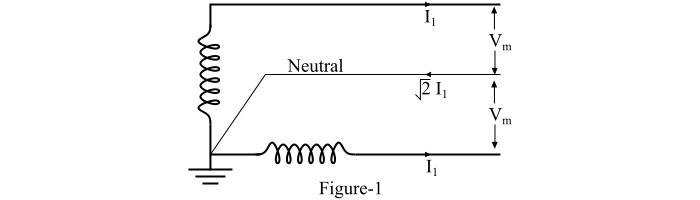
有兩根線導體和一根中性線，中性線取自兩相繞組的連線點，這兩相繞組的電壓彼此正交（即 90°）。很明顯，每根線導體傳輸總電力的二分之一。
因此，任何線導體與中性線（即相電壓）之間的電壓的 RMS 值為：
$$\mathrm{\mathit{V_{ph}\mathrm{\, =\, }\frac{V_{m}}{\sqrt{\mathrm{2}}}}}$$
∴ 每根導體的線電流為：
$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P/\mathrm{2}}{V_{ph}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P/\mathrm{2}}{\frac{V_{m}}{\mathrm{\sqrt{2}}}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P}{\mathrm{\sqrt{2}}V_{m}\, \mathrm{cos}\, \phi} }} $$
中性線中的電流是線電流的相位和，線導體中的電流彼此相差 90°。
$$\mathrm{\mathit{\therefore \mathrm{中性電流,}I_{n}\mathrm{\, =\, }\sqrt{I_{\mathrm{1}}^{\mathrm{2}}\mathrm{\, +\, }I_{\mathrm{1}}^{\mathrm{2}}}\mathrm{\, =\, }\sqrt{\mathrm{2}}I_{\mathrm{1}}}} $$
假設中性線的橫截面積是任一線導體的 √2 倍，以便電流密度保持恆定。
$$\mathrm{\mathit{\therefore \mathrm{中性線電阻,}\, R_{n}\mathrm{\, =\, }\frac{R_{\mathrm{1}}}{\sqrt{\mathrm{2}}}\mathrm{\, =\, }\frac{\rho l}{\sqrt{\mathrm{2}}a_{\mathrm{1}}}}}$$
因此，系統中的匯流排路損耗由下式給出：
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\mathrm{\, +\, }I_{n}^{\mathrm{2}}R_{n}\mathrm{\, =\, }\mathrm{2}I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\mathrm{\, +\, }\left ( \sqrt{\mathrm{2}}I_{\mathrm{1}} \right )^{\mathrm{2}}\frac{R_{\mathrm{1}}}{\sqrt{\mathrm{2}}}\mathrm{\, =\, }I_{\mathrm{1}}^{\mathrm{2}}R_{\mathrm{1}}\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\left ( \frac{P}{\sqrt{\mathrm{2}}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho l}{a_{\mathrm{1}}}\right )\times \left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right ) }} $$
$$\mathrm{\mathit{\therefore W\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )\times P^{\mathrm{2}}\rho l}{\mathrm{2}V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, a_{\mathrm{1}}}}}$$
$$\mathrm{\mathit{\therefore \mathrm{橫截面積}, a_{\mathrm{1}}\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )\times P^{\mathrm{2}}\rho l}{\mathrm{2}\, W\: V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}} $$
因此，兩相三線交流系統中所需的導體材料體積（設為 K）由下式給出：
$$\mathrm{\mathit{K\mathrm{\, =\, }\mathrm{2}\, a_{\mathrm{1}}\, l\mathrm{\, +\, }\sqrt{\mathrm{2}}a_{\mathrm{1}}l\mathrm{\, =\, }a_{\mathrm{1}}l\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )}}$$
$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\left ( \mathrm{2\mathrm{\, +\, }\sqrt{2}} \right )^{\mathrm{2}}\times P^{\mathrm{2}}\rho l^{\mathrm{2}}}{\mathrm{2}\, W\: V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }\mathrm{\, =\, }\frac{\mathrm{5.828}\, P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}\: \: \cdot \cdot \cdot \left ( 1 \right )}$$
兩相四線交流系統中所需的導體材料
圖 2 顯示了兩相四線交流系統。在這個系統中，四根線導線取自兩相繞組的兩端，兩相繞組的中點連線在一起。
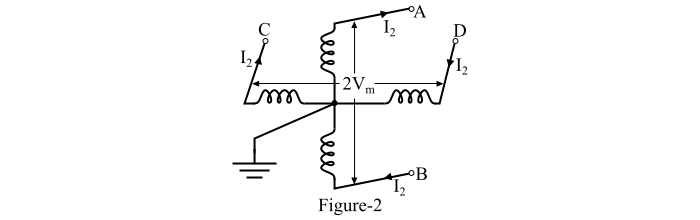
每個相位傳輸總功率 (P) 的二分之一。現在，考慮兩個相位中的一個，例如相位繞組 AB，然後：
$$\mathrm{相位 AB 上的最大電壓\, \mathit{AB\mathrm{\, =\, }\mathrm{2}V_{m}}}$$
$$\mathrm{\therefore 相位 AB 上電壓的 RMS 值\, \mathit{AB\mathrm{\, =\, }\frac{\mathrm{2}V_{m}}{\mathrm{\sqrt{2}}}\mathrm{\, =\, }\mathrm{\sqrt{2}}V_{m}}}$$
並且，
$$\mathrm{相位 AB 供給的功率（即每相功率）\mathrm{\, =\, }\frac{\mathit{P}}{2}}$$
設 cos 𝜙 為負載的功率因數，則
$$\mathrm{每相負載電流\: \mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P/\mathrm{2}}{\sqrt{\mathrm{2}}\, V_{m}\, \mathrm{cos}\, \phi }\mathrm{\, =\, }\frac{P}{\mathrm{2}\sqrt{\mathrm{2}}\, V_{m}\, \mathrm{cos}\, \phi }}}$$
如果 𝑎2 是每根導體的橫截面積，R2 是每根導體的電阻，則匯流排路損耗為：
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{4}\, I_{\mathrm{2}}^{\mathrm{2}}R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{4}\, \times\, \left ( \frac{P}{\mathrm{2\sqrt{2}}V_{m}\, \mathrm{cos}\, \phi} \right )^{\mathrm{2}}\times \frac{\rho l}{a_{\mathrm{2}}} }}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, a_{\mathrm{2}}}}}$$
∴ 橫截面積為：
$$\mathrm{\mathit{a_{\mathrm{2}}\mathrm{\, =\, }\frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}}$$
因此，兩相四線交流系統中所需的導體材料體積（設為 𝐾1）由下式給出：
$$\mathrm{\mathit{K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{4}a_{\mathrm{2}}l\mathrm{\, =\, }\mathrm{4}\times \frac{P^{\mathrm{2}}\, \rho l}{\mathrm{2}W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }\times l}}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, } \frac{\mathrm{2}P^{\mathrm{2}}\, \rho l^{\mathrm{2}}}{W\, V_{m}^{\mathrm{2}}\, \mathrm{cos^{2}}\, \phi \, }}\; \; \; \cdot \cdot \cdot \left ( 2 \right )}$$
比較公式 (1) 和 (2)，得到：
$$\mathrm{\mathit{\frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{2}P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\mathrm{cos^{\mathrm{2}}}\phi } \right )}{\left ( \frac{\mathrm{5.828}P^{\mathrm{2}}\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\mathrm{cos^{\mathrm{2}}}\phi } \right )}\mathrm{\, =\, }\mathrm{0.343}}}$$
$$\mathrm{\therefore \mathit{K_{\mathrm{1}}}\mathrm{\, =\, }0.343\times \mathit{K}\; \; ...\left ( 3 \right )}$$
因此，兩相四線制系統中所需的導體材料體積是兩相三線制系統所需體積的 0.343 倍。
463 次瀏覽
