資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學無失真傳輸系統
失真定義為訊號在透過系統傳輸時形狀的變化。因此，當系統的輸出是輸入訊號的精確複製時，訊號透過系統的傳輸被認為是無失真的。此複製品，即系統的輸出，可能具有不同的幅度，也可能具有不同的時間延遲。
輸出訊號幅度的恆定變化和恆定的時間延遲不被視為失真。只有訊號形狀的變化才被認為是失真。
數學上，如果系統的輸出為，則訊號𝑥(𝑡)的傳輸被認為是無失真傳輸。
$$\mathrm{y(t)=kx(t-t_{d})\; \; \cdot \cdot \cdot (1)}$$
其中，
常數k表示幅度的變化，無論是放大還是衰減。
𝑡𝑑是延遲時間。
無失真系統的框圖以及典型的輸入和輸出波形如圖1所示。
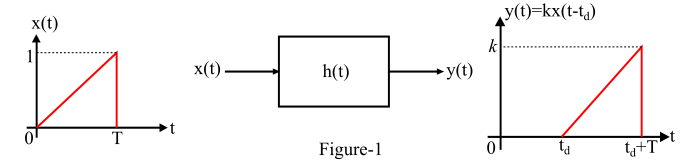
現在，對等式(1)兩邊進行傅立葉變換，並使用傅立葉變換的移位特性，我們得到，
$$\mathrm{Y(\omega )=ke^{-j\omega t_{d}}X\left ( \omega \right )}$$
因此，無失真傳輸系統的傳遞函式由下式給出，
$$\mathrm{H(\omega )=\frac{Y\left ( \omega \right )}{X\left ( \omega \right )}=ke^{-j\omega t_{d}}\; \; \cdot \cdot \cdot (2)}$$
現在，對等式(2)進行傅立葉逆變換，得到系統對應的衝激響應，
$$\mathrm{h(t)=k\delta (t-t_{d})\: \: \cdot \cdot \cdot (3)}$$
傳遞函式的幅度為，
$$\mathrm{\left | H(\omega ) \right |=k}$$
對於所有𝜔值，它都是常數。
傳遞函式的相移為，
$$\mathrm{\theta \left ( \omega \right )=\angle H(\omega )=-\omega t_{d}}$$
一般情況下，相移為，
$$\mathrm{\theta \left ( \omega \right )=n\pi -\omega t_{d};\; \; \left ( n\: is\:an\:integer \right )}$$
並且它隨頻率線性變化。圖2顯示了無失真傳輸系統的幅度和相位特性。
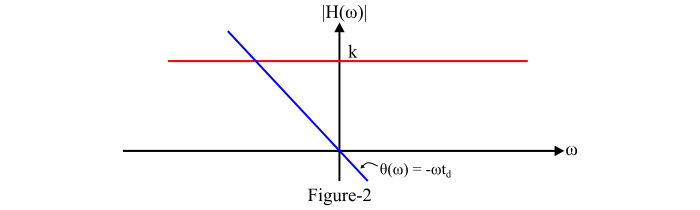
因此，為了使訊號透過系統進行無失真傳輸，系統傳遞函式的幅度|𝐻(𝜔)|應為常數，即輸入訊號必須對所有頻率分量進行相同的放大或衰減。因此，為了實現系統的無失真傳輸，系統的頻寬是無限的，並且相位譜應與頻率成正比。然而，在實踐中，不存在頻寬無限的系統，因此無失真傳輸的條件永遠不會完全滿足。
5K+ 次瀏覽
