譯碼器的級聯

---

什麼是譯碼器？

譯碼器是一種組合邏輯電路，它將 N 位二進位制輸入程式碼轉換為 2^N 條輸出線，使得對於每種可能的輸入組合，只有一條輸出線處於啟用狀態。譯碼器的框圖如圖 1 所示。

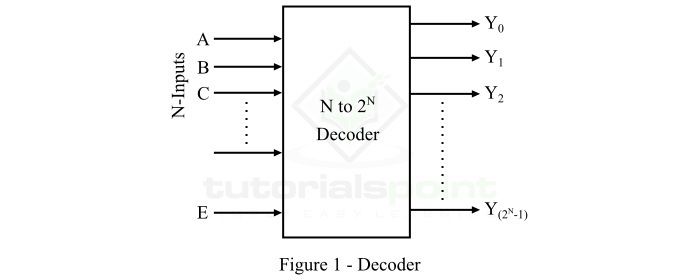
這裡，A、B、C 等是輸入線，Y₀、Y₁、Y₂……等是輸出線，E 是譯碼器的使能輸入。

在本文中，我們將討論譯碼器的級聯。譯碼器的級聯是指透過將低階譯碼器連線在一起來實現更高階譯碼器的過程。

例如，我們可以透過級聯兩個 3 線到 8 線譯碼器來獲得一個 4 線到 16 線譯碼器。在這裡，我們將藉助以下兩個示例來了解譯碼器的級聯：

• 將 2 線到 4 線譯碼器級聯以獲得 3 線到 8 線譯碼器。

• 將 3 線到 8 線譯碼器級聯以獲得 4 線到 16 線譯碼器。

但在進入級聯部分之前，讓我們首先了解一下 2-to-4 線譯碼器、3-to-8 線譯碼器和 4-to-16 線譯碼器的各自資訊。

2-to-4 譯碼器

2-to-4 譯碼器是一種譯碼器電路，它具有 2 條輸入線和 4 (2²) 條輸出線。2-to-4 譯碼器的框圖如下所示（圖 2）。

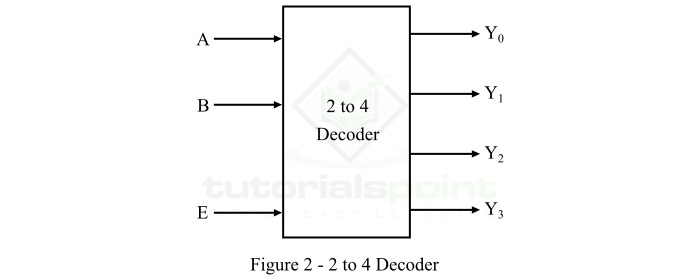
這裡，A 和 B 是兩個輸入，Y₀、Y₁、Y₂ 和 Y₃ 是四個輸出。當使能輸入 E 處於啟用狀態時，對於每種輸入組合，這些輸出線中的一條將處於啟用狀態。

3-to-8 譯碼器

3-to-8 譯碼器是一種譯碼器電路，它具有 3 條輸入線和 8 (2³) 條輸出線。3-to-8 譯碼器的框圖如圖 3 所示。

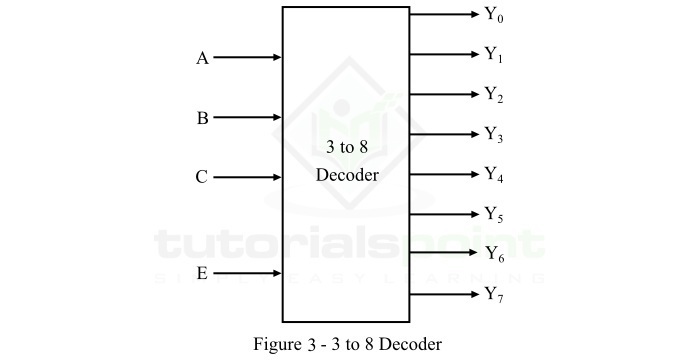
這裡，A、B 和 C 是三個輸入，Y₀、Y₁、Y₂、Y₃、Y₄、Y₅、Y₆ 和 Y₇ 是八個輸出。當使能輸入 E 處於啟用狀態時，對於每種輸入組合，這些輸出線中的一條將處於啟用狀態。

4-to-16 譯碼器

4-to-16 譯碼器是一種譯碼器電路，它具有 4 條輸入線和 16 (2⁴) 條輸出線。4-to-16 譯碼器的框圖如圖 4 所示。

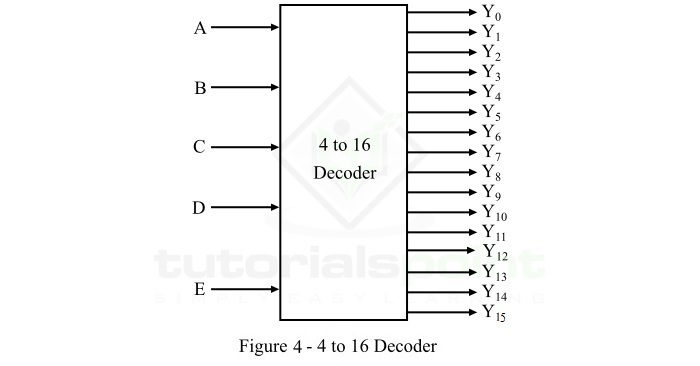
這裡，A、B、C 和 D 是三個輸入，Y₀、Y₁、Y₂、Y₃、Y₄……Y₁₅ 是十六個輸出。當使能輸入 E 處於啟用狀態時，對於每種輸入組合，這些輸出線中的一條將處於啟用狀態。

現在，讓我們討論將較小的譯碼器級聯以獲得較大的譯碼器。

將 2-to-4 譯碼器級聯以獲得 3-to-8 譯碼器

在本節中，我們將瞭解透過級聯 2-to-4 線譯碼器來實現 3-to-8 線譯碼器。

正如我們上面提到的，2-to-4 譯碼器包含兩條輸入線 A 和 B，以及四條輸出線 Y₀ 到 Y₃。另一方面，3-to-8 譯碼器具有三條輸入線 A、B 和 C，以及八條輸出線 Y₀ 到 Y₇。

因此，要獲得更高階譯碼器而需要級聯的低階譯碼器的數量可以透過以下公式確定：

$$ \mathrm{低階譯碼器數量\, =\, \frac{高階譯碼器的輸出數量}{低階譯碼器的輸出數量}}$$

在我們的例子中，低階譯碼器的輸出數量為 4，高階譯碼器的輸出數量為 8。因此，

$$\mathrm{2 - to - 4 譯碼器數量\, =\, \frac{8}{4}\, =\, 2}$$

因此，我們需要級聯兩個 2-to-4 線譯碼器來實現 3-to-8 線譯碼器。透過級聯 2-to-4 線譯碼器獲得的 3-to-8 線譯碼器的邏輯框圖如圖 5 所示。

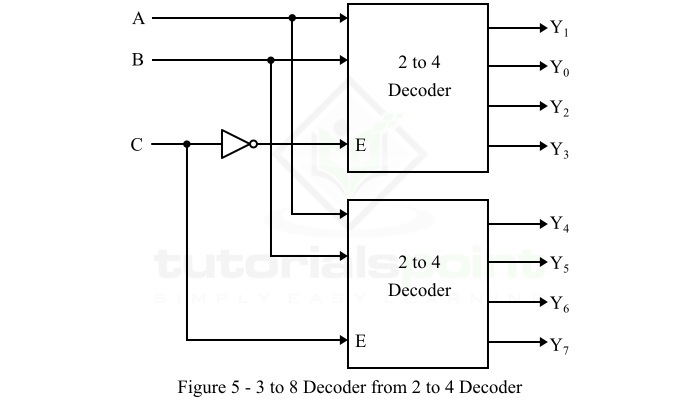
這裡，輸入 A 和 B 並行應用於每個 2-to-4 譯碼器。輸入 C 的補碼連線到上部 2-to-4 譯碼器的使能輸入 E 以獲得輸出 Y₀ 到 Y₃。輸入 C 直接連線到下部 2-to-4 譯碼器的使能輸入 E 以獲得輸出 Y₄ 到 Y₇。

將 3-to-8 譯碼器級聯以獲得 4-to-16 譯碼器

在本節中，我們將討論將 3-to-8 譯碼器級聯以實現 4-to-16 譯碼器。如我們所知，3-to-8 譯碼器具有三個輸入 A、B 和 C，以及八個輸出 Y₀ 到 Y₇。另一方面，4-to-16 譯碼器具有四個輸入 A、B、C 和 D，以及十六個輸出 Y₀ 到 Y₁₅。

因此，要獲得 4-to-16 譯碼器而需要級聯的 3-to-8 譯碼器的數量由以下公式給出：

$$\mathrm{3 - to - 8 譯碼器數量\, =\, \frac{16}{8}\, =\, 2}$$

因此，需要級聯兩個 3-to-8 譯碼器才能獲得 4-to-16 譯碼器。

透過級聯兩個 3-to-8 譯碼器獲得的 4-to-16 譯碼器的邏輯框圖如圖 6 所示。

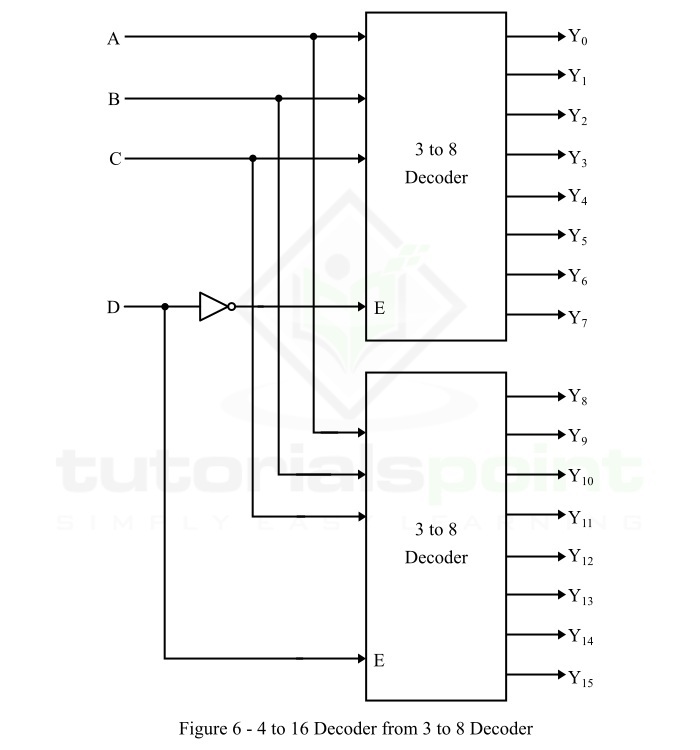
這裡，輸入 A、B 和 C 並行連線到每個 3-to-8 譯碼器。第四個輸入 D 的補碼連線到上部 3-to-8 譯碼器的使能輸入 E 以獲得輸出 Y₀ 到 Y₇。輸入 D 直接應用於下部 3-to-8 譯碼器的使能輸入 E 以獲得輸出 Y₈ 到 Y₁₅。

這就是我們如何透過級聯一組低階譯碼器來實現更高階譯碼器。