資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++中正方形外接圓的面積
在這個問題中，我們將計算已知正方形邊長的正方形外接圓的面積。在進一步討論之前，讓我們回顧一下基本定義，以便更好地理解這些概念。
正方形是一個四邊相等且四個角都為直角的四邊形。
外接圓是一個與多邊形所有頂點相切的圓。
面積是對任何二維圖形範圍的定量表示。
要計算正方形外接圓的面積，我們需要找到圓和正方形引數之間的關係。
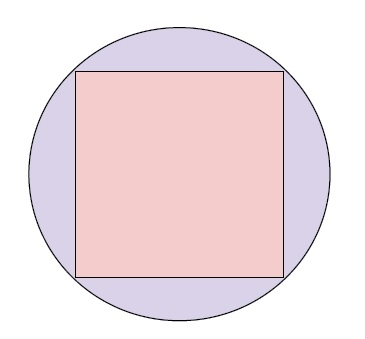
現在，如圖所示，正方形的所有頂點都與圓相切。從圖中可以看出，正方形的對角線等於圓的直徑。
利用這一點，我們可以推匯出圓的直徑和正方形邊長之間的關係。
r = (√ (2a^2))/2
r 是圓的半徑，a是正方形的邊長。
現在，使用公式我們可以找到圓的面積。
Area of circle = π*r^2 = π* ((√ (2a^2))^2 / 2 = π * (2 *a ^ 2)/4 = (π*a^2)/2
現在，使用這個公式，我們可以找到圓的面積。
演算法
Step 1 : Calculate area of circle using formula {(3.14 * a * a) /2 }
Step 2 : Print the area of the circle示例
#include <iostream>
using namespace std;
int main(){
float a = 6;
float area = ( (3.14 * a * a )/2) ;
cout<<"The area of Circumscribed Circle of a Square of side "<<a<<" is "<<area;
return 0;
}輸出
The area of Circumscribed Circle of a Square of side 6 is 56.52
更新於：2019年10月16日
瀏覽量 148
廣告