積分的應用

---

簡介

積分的應用廣泛應用於數學、科學、工程等各個領域。積分的應用在數學和物理學中被廣泛用於各種目的。

• 如果積分應用於曲線下的面積或兩條曲線之間的面積，則稱為**積分的幾何應用**，其中還包括求旋轉體的體積、曲線的長度等。

• 如果積分應用於求物體的重心、質量、動量、位移、速度等，則稱為**積分的物理應用**。

在本教程中，我們將學習積分及其在曲線下面積和兩條曲線之間面積中的應用，並附帶一些已解決的示例。

積分

等於曲線或函式下方的面積的數值可以稱為**積分**。據說它們為解釋面積、體積等的函式分配值，因為它們測量給定區間內的整個空間。

面積 A 由下式給出：

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

積分被稱為找到這些積分的過程。積分有兩種型別，即定積分和不定積分。帶有極限的積分函式稱為定積分。

定積分定義為：

$$\mathrm{I=\int_{x=a}^{x=b}f(x) dx}$$

沒有極限的積分函式稱為不定積分。

不定積分定義為：

$$\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C\: where\: C\: is\: a\: constant.}$$

積分的應用：曲線下面積

曲線 f(x) 下方的面積 A 在區間 [a, b] 內。我們需要在 a 和 b 的限制範圍內對 f(x) 進行積分以找到 f(x) 下方的 A。由於積分函式具有限制 a 和 b，因此 f(x) 被稱為定積分。

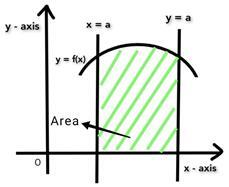
計算曲線下面積的公式由下式給出：

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

兩條曲線之間的面積

兩條曲線 f(x) 和 g(x) 在兩點處相交。交點為 x= a 和 x=b，我們顯然知道它們是 x 座標。兩條曲線在其之間包圍了一個區域 A。

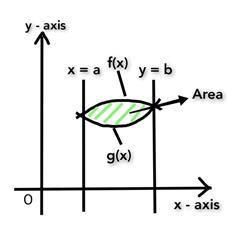
• 如果曲線 f(x) 高於 g(x)，使得對於 a≤ x ≤b，f(x) ≤g(x)，則

  求兩條曲線之間面積的公式由下式給出：

  $$\mathrm{A = \int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

• 如果曲線 g(x) 高於 f(x)，使得對於 a≤ x ≤b，g(x) ≤f(x)，則

  求兩條曲線之間面積的公式由下式給出：

  $$\mathrm{A = \int_{x=a}^{x=b}g(x) dx-\int_{x=a}^{x=b}f(x) dx}$$

已解決的示例

1)求函式 f(x)=(x⁴+6) 曲線下的面積 A，給定限制為 2≤ x ≤3。

答案

計算曲線下面積的公式由下式給出：

曲線下的面積 = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

給定曲線下的面積 = $\mathrm{\int_2^3(x^4+6) dx}$

給定曲線下的面積 = $\mathrm{[\frac{x^5}{5}+6x]_{x=2}^{x=3}}$

給定曲線下的面積 = $\mathrm{[\frac{3^5}{5}-\frac{2^5}{5}] +[6(3)-6(2)]}$

給定曲線下的面積 = $\mathrm{[\frac{243-32}{5}] +[18-12]}$

給定曲線下的面積 =$\mathrm{\frac{211}{5}+6}$

給定曲線下的面積 = $\mathrm{\frac{211+30}{5}}$

給定曲線下的面積 = $\mathrm{\frac{241}{5}}$

給定曲線下的面積 = 48.1 平方單位。

因此，函式 (x⁴+6) 曲線下的面積為 48.1 平方單位。

2)求給定兩條曲線 f(x)=3x 和 g(x)=2x 之間的面積 A，給定限制為 0≤ x ≤3。

答案

求兩條曲線之間面積的公式由下式給出：

兩條曲線之間的面積 $\mathrm{= \int_{x=a}^{x=b} f(x) dx-\int_{x=a}^{x=b}g(x) dx}$

給定曲線之間的面積 $\mathrm{= \int_0^3(3x-2x) dx}$

給定曲線之間的面積 = $\mathrm{\int_0^3x dx}$

給定曲線之間的面積 = $\mathrm{[\frac{x^2}{2}]_{x=0}^{x=3}}$

給定曲線之間的面積 = $\mathrm{\frac{(3)^2}{2}-0}$

給定曲線之間的面積 = $\mathrm{\frac{9}{2}}$

給定曲線之間的面積 = 4.5 平方單位。

因此，給定兩條曲線 f(x)=3x 和 g(x)=2x 之間的面積 A 為 4.5 平方單位。

3)求函式 f(x)=(5x-x^2) 曲線下的面積 A，給定限制為 0≤ x ≤5。

答案

計算曲線下面積的公式由下式給出：

曲線下的面積 = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

給定曲線下的面積 = $\mathrm{\int_0^5(5x-x^2) dx}$

給定曲線下的面積 =$\mathrm{[\frac{5x^2}{2}+\frac{x^3}{3}]_{x=0}^{x=5}}$

給定曲線下的面積 = $\mathrm{[\frac{5(5)^2}{2}-\frac{5^3}{3}] -0}$

給定曲線下的面積 = $\mathrm{[\frac{125}{2}-\frac{125}{3}] -0}$

給定曲線下的面積 = $\mathrm{\frac{(3×125) - (2×125)}{6}}$

給定曲線下的面積 = $\mathrm{\frac{375 - 250}{6}}$

給定曲線下的面積 = $\mathrm{\frac{125}{6}}$

給定曲線下的面積 = 20.833 平方單位。

因此，函式 $\mathrm{\int_0^5(5x-x^2) dx}$ 曲線下的面積為 20.833 平方單位。

4)求給定兩條曲線 f(x)=x⁴ 和 g(x)=x 之間的面積 A，給定限制為 2≤ x ≤3。

答案

求兩條曲線之間面積的公式由下式給出：

$$\mathrm{A=\int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

$$\mathrm{A=\int_2^3(x^4-x) dx}$$

$$\mathrm{A=[\frac{x^5}{5}-\frac{x^2}{2}]_{x=2}^{x=3}}$$

$$\mathrm{A=[\frac{3^5- 2^5}{5}]-[\frac{3^2-2^2}{2}]}$$

$$\mathrm{A=[\frac{243- 32}{5}]-[\frac{9-4}{2}]}$$

$$\mathrm{A=\frac{211}{5}-\frac{5}{2}}$$

$$\mathrm{A=\frac{422-25}{10}}$$

$$\mathrm{A=\frac{397}{10}}$$

$$\mathrm{A=39.7\: 平方單位.}$$

因此，給定兩條曲線 f(x)=x⁴ 和 g(x)=x 之間的面積 A 為 39.7 平方單位。

結論

• 曲線下方的面積表示定義為積分。

• 定積分 I 由下式給出：

  $$\mathrm{I= \int_{x=a}^{x=b}f(x) dx}$$

• 沒有極限的積分函式，例如 $\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C}$，稱為不定積分。

• 計算曲線下面積的公式由下式給出：

  $$\mathrm{A =\int_{x=a}^{x=b}f(x) dx}$$

• 求兩條曲線之間面積的公式由下式給出：

  $$\mathrm{面積=\int_{x=a}^{x=b}[f(x) -g(x)]dx}$$

常見問題解答

1. 哪些被認為是微積分的重要工具？

微積分的重要工具是積分、極限和導數。

它們的作用是描述函式的行為，然後對其進行分析。

歷史上，在 17 世紀後期，著名的數學家艾薩克·牛頓爵士和戈特弗裡德·萊布尼茨發現了微積分，因為他們為導數和微分的理論發展做出了貢獻。

2. 誰引入了分部積分？

英國數學家布魯克·泰勒以泰勒級數和定理而聞名，他是發現分部積分的人。由於這位偉大的數學家，我們有了一個新的分支，稱為有限差分微積分。

3. 什麼是曲面積分？

在彎曲的二維區域或平面上的積分稱為曲面積分。

要定義函式 $\mathrm{\underline{F}}$ 的曲面積分，整個表面 S 被分成小的表面元素 ΔS。

$$\mathrm{\int F⋅ds=\lim_{n \rightarrow ∞} \sum_{i=1}^{n}\underline{F_i}\: \underline{ΔS_i} , \: ΔS→0}$$

4. 什麼是線積分？

如果沿曲線計算積分的函式，則該積分稱為線積分。

它也可以稱為路徑積分。

5. 重積分和曲面積分有什麼區別？

在平坦的二維平面上的積分是重積分。而在彎曲的二維平面上的積分是曲面積分。