定積分的性質

---

引言

積分有兩種方法：

• 確定積分和

• 不定積分。

定積分是在由邊界指定的邊界或區域上進行的。由於曲線是有限的，因此曲線下的面積也被認為是有限的，但不定積分用於沒有上限或下限的函式，但由於函式本質上是無限的，因此上限和下限是不確定的。函式 + ∞ & -∞。

積分

• 在微積分中，我們關注的是尋找可微函式的導數（或微分）的方法。

• 我們能否解決逆問題？也就是說，如果函式具有給定的導數（或微分）？例如，函式 y=x⁶ 的導數是 $\mathrm{\frac{dy}{dx}=6x^5}$（或其微分是 $\mathrm{dy=6x^5 dx }$）。因此，很容易理解具有導數 $\mathrm{6x^5}$（或微分 $\mathrm{6x^5 dx}$）的函式是 x⁶ 。

• 在這種情況下，從導數 dy/dx=6x^5（或微分 dy=6x^5 dx）確定函式 y=x⁶ 的數學方法稱為積分。

• 透過積分從函式的導數（或微分）獲得的函式稱為其積分。在上例中，$\mathrm{\frac{dy}{dx}=6x^5}$（或 $\mathrm{dy=6x^5 dx }$）的積分是 y=x⁶。顯然，積分可以看作是反導數，即它是微分的逆過程。

定積分

如果在任何數學研究中的量都可以表示為一個級數的形式，透過根據某種規律或規則將其分成幾個部分，使得級數的項數可以無限增加，並且級數的每一項都無限小，那麼這樣的級數的和的極限值稱為定積分。

定積分作為和的極限

設 f(x) 是在有限區間 a≤x≤b 上定義的有界單值連續函式。現在，用點 a, a+h, a+2h,…., a+(n-1)h … a+nh 將區間 a≤x≤b 分成 n 個等長的子區間，每個子區間的長度為 h，其中 a+nh=b，或 nh=b-a。然後，極限（如果存在），

$$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h[\mathit{f}(a)+\mathit{f}(a+h)+\mathit{f}(a+2h)[\mathit{f}(a)\mathit{f}(a+(n-1)h)]]}$$

或者簡而言之，$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$ 稱為 f(x) 關於 x 從 a 到 b 的定積分，用符號表示。

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x }$$

這裡 b 稱為積分的上限或上界，a 稱為其下限或下界。因此，

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x =\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$$

其中 nh=b-a，前提是極限存在。

在數學中，簡單的求和和加法很容易，但是當涉及到計算複雜的積分時，簡單的計算和加法是不夠的，需要積分。在計算定積分時，計算可能很繁瑣和複雜，因此使用經驗上證明的性質可以使計算相對容易。

曲線下面積的定積分

假設我們想找到由連續曲線 y=x²、x 軸、縱座標 x=1 和縱座標 x=4 圍成的面積。

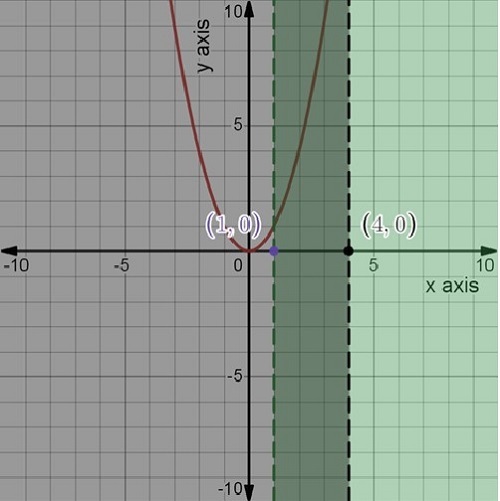
顯然，可以透過將區間 1≤x≤4 分成 10 個等長的子區間，用點 x=1, 1.3, 1.6,…劃分，並在每個細分點處豎起縱座標，將該面積分成 10 部分。因此，封閉面積可以表示為 10 項級數的形式。類似地，如果區間 1≤x≤4 被分成 100 個等長的子區間，用點 x=1, 1.03, 1.06,…劃分，並在每個細分點處豎起縱座標，那麼封閉面積可以表示為 100 項級數的形式。

定積分的性質

定積分的性質：

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(t) d(t)}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=-\int_{b}^{a}\mathit{f}(x) dx}$

• $\mathrm{\int_{a}^{a}\mathit{f}(x) d x=0}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{c}\mathit{f}(x) d x+\int_{c}^{b}\mathit{f}(x) d x}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a + b – x) d x}$

• $\mathrm{\int_{0}^{a}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a – x) d x}$

例題

1. 計算 $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}}$

因為，

$$\mathrm{\int\frac{dx}{x(1+logx)^2}=-\frac{1}{z}=-\frac{1}{1+logx}}$$

因此，$\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=-[\frac{1}{1+logx}]_1^e=-[\frac{1}{1+loge}-\frac{1}{1+log1}]=-(\frac{1}{2}-1)=\frac{1}{2}}$

因此， $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=\frac{1}{2}}$。

2. 如果 $\mathrm{\mathit{f}(x)=\mathit{f}(a+x)}$，則證明 $\mathrm{\int_a^{a+t} \mathit{f}(x)dx }$ 與 a 無關。

我們令 x=a+z；因此，dx=dz。

同樣，當 x=a 時，z=0；當 x=a+t 時，z=t。

因此，

$\mathrm{ \int_a^{a+t} f(x)dx=\int_0^t f(a+z)dz=\int_0^t f(a+x)dx=\int_0^t f(x)dx }$，它與 a 無關。

證畢。

3. 計算以下定積分：$\mathrm{ \int_{-a}^a \frac{dx}{x^a+a^2}}$。

$$\mathrm{\int_{-a}^a \frac{dx}{x^a+a^2}=\frac{1}{a}[tan^{-1} \frac{x}{a}]^a_{-a}=\frac{1}{a}[tan^{-1} \frac{a}{a}-tan^{-1} \frac{-a}{a}]}$$

$$\mathrm{=\frac{1}{a}[tan^{-1} 1-tan^{-1} (-1)]=\frac{1}{a}[\frac{π}{4}-(-\frac{π}{4})]=\frac{π}{2a}}$$

因此，$\mathrm{\int_{-a}^a \frac{ dx}{x^a+a^2}=\frac{π}{2a}}$

結論

積分，顧名思義，用於整合某些東西。在數學中，積分是一種整合函式的方法。積分的另一個術語可以是求和，或者是一種圖形化的方式來查詢曲線函式下的面積，用於總結整個函式。積分被稱為導數的反面，函式分解成更小的函式，積分將較小的部分相加以獲得曲線下的總面積。以級數的形式封閉的面積，其項數可以越來越大，每一項的值越來越小。在這種情況下，這樣的級數的和的極限值稱為定積分。

常見問題

1. 什麼是定積分？

定積分定義了曲線下方在兩個固定極限之間的面積。這表示為 ∫a.0f (x) dx。其中 a 和 b 分別是定義在 x 軸上的函式 f (x) 的下限和上限。

2. 如何計算定積分？

定積分的計算方法如下：

步驟 1：找到不定積分的積分。

步驟 2：將極限應用於結果

步驟 3：代入上限和下限，然後減去得到的值。

3. 計算特定積分時首先要考慮什麼？

要計算定積分，必須首先計算函式的不定積分。因此，計算定積分時首先要考慮的是取定積分並進行積分。

4. 如何用圖形方法計算定積分？

定積分的計算是求曲線下方面積。為了找到兩個邊界之間曲線下方的面積，將面積分成矩形並求和這些面積。矩形越多，面積越精確。因此，將面積分成無限多個大小相同（非常小）的矩形，並將所有面積相加。

5. 如何計算定積分？

定積分可以使用多種方法進行計算。計算定積分的各種方法：

• 基本分析定理

• 用代換法計算定積分

• 用圖形法計算定積分

• 用幾何法計算定積分

• 用性質計算定積分

6. 定積分的目的是什麼？

定積分的一些應用：

• 可以使用定積分來求曲線下方以及兩條曲線之間的面積。

• 可以使用定積分來確定 3D 物體的體積。

• 使用定積分計算曲線的弧長。

• 力函式積分也可用於確定功。

• 浸沒在液體中的物體所受的力也可以用定積分來計算。