線性圖的應用

---

引言

線性圖的應用在日常生活中隨處可見。形如直線Ax+By+C=0的圖稱為線性圖。在標準的直線方程中，A和B是係數，x和y是變數，C是常數。

簡單來說，線性圖表示兩個或多個變數之間的關係。透過將方程的變數（例如x、y、z等點）繪製在圖上，我們得到一條直線。線性圖的應用廣泛應用於分析和預測各個科學領域中的未來事件。

在本教程中，我們將學習線性圖及其應用，並附帶一些已解決的問題。

線性圖

表示兩個或多個變數之間關聯的圖表或圖形稱為線性圖。變數也可以被視為數量。

它們用於顯示一段時間內一系列資料點的變化。

例如：

下表給出了X先生2000年至2005年的年收入。

年份	2000	2001	2002	2003	2004
年收入（百萬）	1.5	2.5	3.6	5	6.5

線性圖的應用

• 線性圖用於根據時間查詢運動物體的位移、速度、速度、距離等。

• 線性圖還可以表示一段時間內的資金和支出或收入。

• 在製藥研究中，透過應用線性圖可以找到藥物的精確效力。

• 可以藉助線性圖繪製一個人根據身高估算體重的圖表。

• 可以透過線性圖讀取特定研究中觀察到的人或地方的一組攝氏度轉換為華氏度的值。

• 該圖還可以顯示一段時間內特定國家的人口數量。

• 可以透過線性圖研究一段時間內自然資源的消耗情況。

已解決的例子

1)對於給定方程2x-y=2，提供一組x值x=2,4,6,8和10，求相應的y值，並在線性圖中表示這些值。

答案

將x值代入給定方程2x-y=2，我們得到

$$\mathrm{2(2)-y=2}$$

$$\mathrm{4-y-2=0}$$

$$\mathrm{\Rightarrow y= 2}$$

$$\mathrm{2(4)-y=2}$$

$$\mathrm{8-y-2=0}$$

$$\mathrm{\Rightarrow y= 6}$$

$$\mathrm{2(6)-y=2}$$

$$\mathrm{12-y-2=0}$$

$$\mathrm{\Rightarrow y= 10}$$

$$\mathrm{2(8)-y=2}$$

$$\mathrm{16-y-2=0}$$

$$\mathrm{\Rightarrow y= 14}$$

$$\mathrm{2(10)-y=2}$$

$$\mathrm{20-y-2=0}$$

$$\mathrm{\Rightarrow y= 18}$$

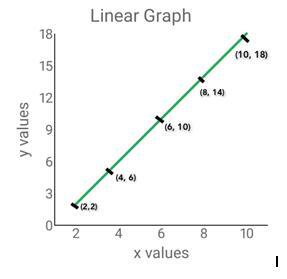
將x和y值製成表格，我們得到

x	2	4	6	8	10
y	2	6	10	14	18

透過繪製上述點，我們得到一個線性圖

2)將給定點繪製在圖上，

x	1	2	3	4	5
y	0	4	7	10	13

答案

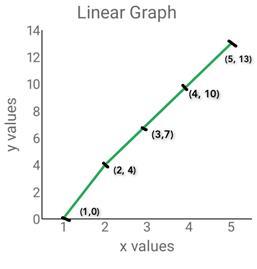
因此，上圖顯示了給定的x和y值。

3)根據下圖的線性圖，將x和y值製成表格。

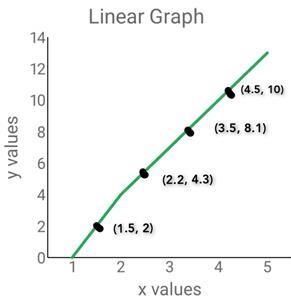
答案

當對上圖中給出的x和y值製表時，我們得到

x	1.5	2.2	3.5	4.5
y	2	4.3	8.1	10

4)弗雷德開車4.8小時行駛11.9公里到達目的地。讓我們閱讀他的遊記以瞭解更多詳情。

當弗雷德開始駕車時，他行駛2.5小時後第一次休息。到那時，他已經行駛了4.4公里。然後他以3小時行駛6.2公里，3.5小時行駛8公里，3.8小時行駛8.5公里，最後以11.9公里到達目的地。將給定資料表示為圖形。所得圖形是線性的嗎？

答案

因此，我們以圖形方式表示了給定資料。是的，所得圖形是線性的。

5)X公司產量增長率如下所示。

根據給定的線性圖，找出以下內容

• 哪一年產品的生產率提高到3.6？

• (b) 2003年X公司的產品生產率是多少？

答案

• 從給定的線性圖可以看出，2002年產品的生產率提高到3.6。

• 2003年X公司的產品生產率為5。

結論

• 直線的通式為Ax+By+C=0。

• 次數為一的方程稱為線性方程。

• 如果圖上繪製的點形成一條直線，則稱其為線性。

• 如果次數為一的方程表示為圖或直線，則稱其為線性。

• 線性圖表示兩個或多個變數之間的關係。

常見問題

1. 如果線性方程寫成y = mx +b的形式怎麼辦？

如果線性方程的形式為y = mx + b，則稱為直線的斜率或y截距。此形式也稱為斜率截距式或斜率截距方程。此外，它被稱為直線的通式。

2. 線性方程中的有序對是什麼？

有序對以(x,y)的形式表示。它包含繪製的或獲得的x和y座標。它被稱為給定線性方程組的解。

3. 我們如何判斷給定的線性方程組是否一致？

在圖中，如果我們發現給定線性方程組的繪製值形成任何交點或重合，則給定的線性方程對是一致的。

4. 一致線性方程組的唯一解和無限解之間有什麼區別？

在圖中，如果我們發現方程的值有一個交點，則解是唯一的。

同樣，在圖中，如果方程的值只形成一個重合點，則可以肯定的是，給定的一致線性方程對有無限多個解。

5. 解線性方程的圖形表示法是什麼？

用消元法解出的給定線性方程組的值的圖形表示也可以稱為解線性方程的圖形法。

如果我們繪製第一個方程的圖形，然後繪製後續方程，則直線將在四個象限之一的點(x,y)處相交。該點將是透過代入法或交叉相乘法獲得的精確解。

6. 線性圖和線圖有什麼區別？

• 連線以形成線性圖的點集是共線的。

• 連線以形成線圖的點集可能不是共線的。