路燈燈泡固定在離街道地面 6 米高的杆子上。如果一個身高 1.5 米的婦女投下的影子長 3 米，求她離電線杆底部的距離。

已知條件

路燈燈泡固定在離街道地面 6 米高的杆子上。

一個身高 1.5 米的婦女投下的影子長 3 米。

要求

我們需要求出她離電線杆底部的距離。

解答

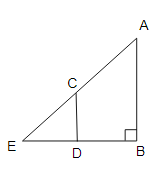
設 A 為固定在杆子上的路燈燈泡的位置，AB = 6 米，CD = 1.5 米為婦女的身高，她的影子為 ED = 3 米。

設電線杆和婦女之間的距離為 x 米。

這裡，

CD ∥ AB

在△CDE 和△ABE 中，

∠E = ∠E (公共角)

∠ABE = ∠CDE = 90°

因此，根據 AA 相似性，

△CDE ∼ △ABE

這意味著，

ED/EB = CD/AB

3/(3+x) = 1.5/6

3 × 6 = 1.5(3+x)

18 = 1.5(3) + 1.5x

1.5x = 18 - 4.5

x = 13.5/1.5

x = 9 米

因此，她離電線杆底部的距離為 9 米。

教程點

更新於：2022年10月10日

65 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習