x = t 時刻的位置
x= t²- 2t
求前 1 秒和 2 秒內的距離和位移。

如給定，$x$ = $t$ 時刻的位置

$x=t^2-2t$

因此，速度 $v=\frac{dx}{dt}=2t-2$

讓我們檢查不同時間間隔的速度符號。

當 $t=0$ 時，$v=-2\ unit/s$

當 $t=1\ s$ 時，$v=2\times1-2=0\ unit/s$

當 $t=2\ s$ 時，$v=2\times2-2=2\ unit/s$

當 $t=0$ 時，$x=0$

當 $t=1\ s$ 時，$x=1^2-2\times 1=1-2=-1$

當 $t=2\ s$ 時，$x=2^2-2\times2=4-4=0$

因此，我們可以說在第一秒內，物體向負 x 軸移動了 1 個單位。並在前 2 秒內返回到正 x 軸，如圖形所示。

因此，前 1 秒內的位移 = 位置變化 = 1 個單位

物體在前 1 秒內移動的距離 = 1 個單位

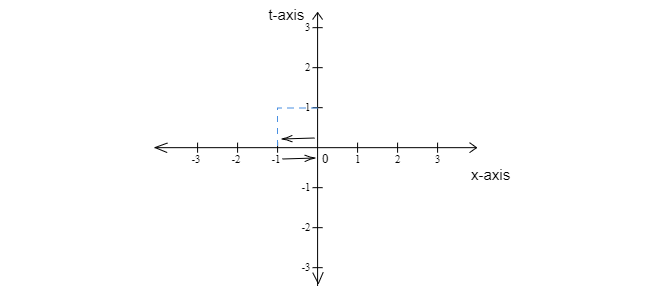
在前 2 秒內，$x=0$ 表示物體返回到 0，朝向正 x 軸。

因此，位移 = 0，因為物體返回到其初始位置。

在前 2 秒內，移動的距離 = 移動路徑的總長度 = 1 個單位 + 1 個單位 = 2 個單位

教程點

更新於: 2022 年 10 月 10 日

32 次瀏覽

開啟您的 職業生涯

完成課程獲得認證

開始學習