什麼是傅立葉頻譜？ - 理論與示例

週期函式 $x(t)$ 的傅立葉係數與頻率 (ω) 之間繪製的圖形稱為週期訊號的**傅立葉頻譜**。

週期函式的傅立葉頻譜有兩個部分 -

• 幅度譜 - 週期訊號的幅度譜定義為傅立葉係數的幅度與頻率的曲線圖。

• 相位譜 - 傅立葉係數的相位與頻率的曲線圖稱為訊號的相位譜。

幅度譜和相位譜一起稱為週期訊號 $x(t)$ 的傅立葉頻率譜。這種週期訊號的表示方法稱為頻域表示。

傅立葉頻率譜只存在於離散頻率處，即在 ，其中，n = 0, 1, 2, 3,… 。因此，傅立葉頻率譜也稱為離散譜或線譜。傅立葉頻率譜的包絡僅取決於脈衝的形狀，而不取決於重複週期。

週期函式 $x(t)$ 的三角傅立葉級數表示包含正弦和餘弦項，以及正負幅度係數 $a_{n}$ 和 $b_{n}$，但沒有相位角。

單邊譜

週期訊號 x(t) 的餘弦傅立葉級數表示僅具有正幅度係數 $A_{n}$ 和相位角 $\theta_{n}$。因此，我們可以繪製幅度譜（$A_{n}$ 與 $\omega$）和相位譜（$\theta_{n}$ 與 $\omega$）。

在餘弦表示中，傅立葉係數僅存在於正頻率處。因此，該頻譜稱為單邊譜。

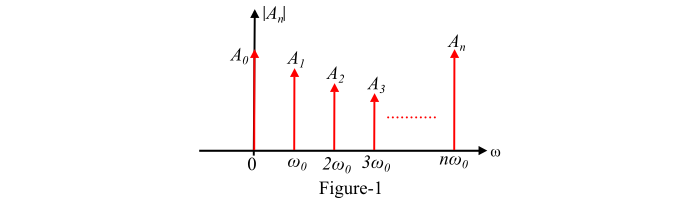
圖-1 表示從 0 到 ∞ 擴充套件的三角（餘弦）傅立葉級數的頻譜，產生單邊譜，因為此表示中不存在負頻率。

雙邊譜

週期函式 $x(t)$ 的指數傅立葉級數表示具有幅度係數 $C_{n}$，它們是複數，可以用幅度和相位表示。因此，我們可以繪製幅度譜（$|C_{n}|$ 與 $\omega$）和相位譜（$\angle C_{n}\:versus\:\omega$）。

在指數表示中，可以繪製正負頻率的頻譜。因此，該頻譜稱為雙邊譜。

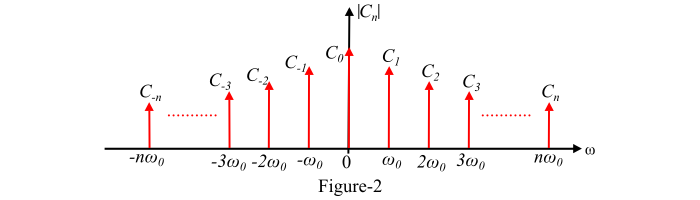
圖-2 表示從 (−∞ 到 ∞) 擴充套件的復指數傅立葉級數的頻譜，產生雙邊譜。

此外，如果 $C_{n}$ 是複數，則

$$\mathrm{C_{n}=|C_{n}|e^{j\theta_{n}}}$$

$$\mathrm{C_{-n}=|C_{n}|e^{-j\theta_{n}}}$$

以及

$$\mathrm{C_{n}=|C_{-n}|}$$

因此，指數傅立葉級數的幅度譜關於透過原點的垂直軸對稱，即幅度譜表現出偶對稱，而相位譜關於透過原點的垂直軸反對稱，即相位譜表現出奇對稱。

此外，當週期訊號 $x(t)$ 為實數時，則

$$\mathrm{C_{-n}=C_{n}^{*}}$$

即 $C_{-n}$ 是指數係數 $C_{n}$ 的複共軛。

數值示例

週期函式的指數傅立葉級數由下式給出：

$$\mathrm{x(t)=\sum_{n=−\infty}^{\infty}\frac{2A}{\pi(1-4n^{2})}e^{j2nt}=\frac{2A}{\pi}+\frac{2A}{\pi}\sum_{\substack{n=-\infty\ n
eq 0}}^{\infty}\left ( \frac{e^{j2nt}}{1-4n^{2}} \right ) }$$

繪製給定函式的頻率譜。

解答

給定的指數傅立葉級數為：

$$\mathrm{x(t)=\sum_{n=−\infty}^{\infty}\frac{2A}{\pi(1-4n^{2})}e^{j2nt}=\frac{2A}{\pi}+\frac{2A}{\pi}\sum_{\substack{n=-\infty\ n
eq 0}}^{\infty}\left ( \frac{e^{j2nt}}{1-4n^{2}} \right )}$$

這裡，指數傅立葉係數為 -

$$\mathrm{C_{0}=\frac{2A}{\pi}\:\:and\:\:C_{n}=\frac{2A}{\pi(1-4n^{2})}}$$

因此，

$$\mathrm{C_{1}=C_{-1}=\frac{2A}{\pi[1-4(1)^{2}]}=-\frac{2A}{3\pi}}$$

$$\mathrm{C_{2}=C_{-2}=\frac{2A}{\pi[1-4(2)^{2}]}=-\frac{2A}{15\pi}}$$

$$\mathrm{C_{3}=C_{-3}=\frac{2A}{\pi[1-4(3)^{2}]}=-\frac{2A}{35\pi}}$$

$$\mathrm{C_{4}=C_{-4}=\frac{2A}{\pi[1-4(4)^{2}]}=-\frac{2A}{63\pi}}$$

等等…

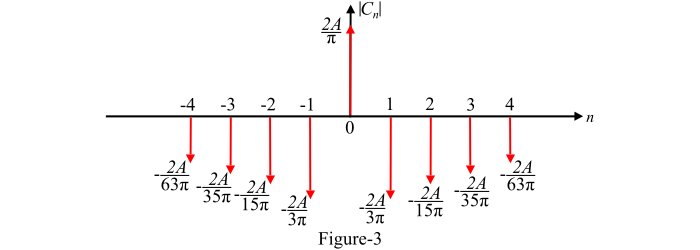
因此，給定函式的頻率譜可以繪製如圖-3 所示。

Manish Kumar Saini

更新於： 2021-12-06

12K+ 次檢視

開啟您的 職業生涯

透過完成課程獲得認證

立即開始