資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究什麼是雙勵系統？
雙勵系統是一種磁系統，其中使用兩個獨立的線圈產生磁場。雙勵系統的例子包括同步電機、他勵直流電機、揚聲器、轉速錶等。
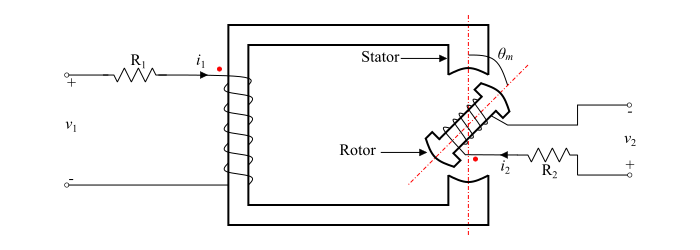
考慮如圖所示的雙勵系統，它由一個定子線圈（電阻為 R1）和一個轉子線圈（電阻為 R2）組成。這兩個線圈由獨立的電壓源激勵。
為了分析雙勵系統，做出以下假設：
對於任何轉子位置，磁鏈 (ψ) 與電流之間的關係都是線性的。
忽略磁滯和渦流損耗。
線圈的漏磁通可忽略不計。
忽略電場，磁場占主導地位。
兩個繞組的磁連結串列達式如下：
$$\mathrm{ψ_{1} = L_{1}i_{1}+ Mi_{2}}$$
$$\mathrm{ψ_{2} = L_{2}i_{2}+ Mi_{1}}$$
應用 KVL，兩個線圈的瞬時電壓方程為：
$$\mathrm{V_{1}=i_{1}R_{1}+\frac{d ψ_{1}}{dt}}$$
$$\mathrm{V_{2}=i_{2}R_{2}+\frac{d ψ_{2}}{dt}}$$
將 $ψ_{1}$ 和 $ψ_{2}$ 的值代入相應的電壓方程，得到：
$$\mathrm{v_{1}=i_{1}R_{1}+\frac{d}{dt}(L_{1}i_{1}+Mi_{2})=i_{1}R_{1}+\frac{d}{dt}(L_{1}i_{1})+\frac{d}{dt}(Mi_{2})\:\:\:\:\:\:...(1)}$$
$$\mathrm{v_{2}=i_{2}R_{2}+\frac{d}{dt}(L_{2}i_{2}+Mi_{1})=i_{1}R_{1}+\frac{d}{dt}(L_{1}i_{1})+\frac{d}{dt}(Mi_{1})\:\:\:\:\:\:...(2)}$$
由於電感取決於轉子角度 $θ_{m}$ 的位置，而 $θ_{m}$ 是時間的函式，且與電流無關。類似地，電流是時間的函式，與電感無關。因此，方程 (1) 和 (2) 可以寫成：
$$\mathrm{v_{1}=i_{1}R_{1}+L_{1}\frac{d i_{1}}{dt}+i_{1}\frac{dL_{1}}{dt}+M\frac{d i_{2}}{dt}+i_{2}\frac{d M}{dt}\:\:\:\:\:\:...(3)}$$
$$\mathrm{v_{2}=i_{2}R_{2}+L_{2}\frac{d i_{2}}{dt}+i_{2}\frac{dL_{2}}{dt}+M\frac{d i_{2}}{dt}+i_{1}\frac{d M}{dt}\:\:\:\:\:\:...(4)}$$
現在，將方程 (3) 乘以 $i_{1}$，方程 (4) 乘以 $i_{2}$，得到：
$$\mathrm{v_{1}i_{1}=i_{1}^{2}R_{1}+L_{1}i_{1}\frac{d i_{1}}{dt}+i_{1}^{2}\frac{dL_{1}}{dt}+Mi_{1}\frac{d i_{2}}{dt}+i_{1}i_{2}\frac{d M}{dt}\:\:\:\:\:\:...(5)}$$
$$\mathrm{v_{2}i_{2}=i_{2}^{2}R_{1}+L_{2}i_{2}\frac{d i_{2}}{dt}+i_{2}^{2}\frac{dL_{1}}{dt}+Mi_{2}\frac{d i_{2}}{dt}+i_{1}i_{2}\frac{d M}{dt}\:\:\:\:\:\:...(6)}$$
方程 (5) 和 (6) 是兩個線圈的功率表達式。
現在，對方程 (5) 和 (6) 關於時間積分並相加，得到：
$$\mathrm{\int(v_{1}i_{1}+v_{2}i_{2})dt=\int(i_{1}^2R_{1}+i_{1}^2R_{1})dt+\int(l_{1}i_{1}di_{1}+l_{2}i_{2}di_{2}+i_{1}^2dL_{1}+i_{2}^2dL_{2}+Mi_{1}di_{2}+Mi_{2}di_{1}+2i_{1}i_{2}dM)\:\:\:\:\:\:...(7)}$$
方程 (7) 是雙勵磁系統的能量方程。它表明，輸入到系統的總電能等於兩部分之和，其中第一部分是電能損耗的能量，第二部分是有用電能，即：
$$\mathrm{[總電能輸入\: W_{e}] = [電能損耗能量\: W_{electric.losses}]+[有用電能\: W_{f}+W_{m}]}$$
其中，
$$\mathrm{W_{f}+W_{m}=\int(l_{1}i_{1}di_{1}+l_{2}i_{2}di_{2}+i_{1}^2dL_{1}+i_{2}^2dL_{2}+Mi_{1}di_{2}+Mi_{2}di_{1}+2i_{1}i_{2}dM)\:\:\:\:\:\:...(8)}$$
儲存在磁場中的能量
儲存在磁場中的能量的瞬時值取決於電感和該時刻電流的值。對於轉子的任何靜止位置，機械輸出為零，所有有用的電能輸入都轉換為場能。由於電感值是恆定的，因此 $dL_{1}$、$dL_{2}$ 和 dM 項變為零。因此，從方程 (8) 中，我們得到：
$$\mathrm{\int dW_{f}=\int_{0}^{i_{1}}L_{1}i_{1}di_{1}+\int_{0}^{i_{2}}L_{2}i_{2}di_{2}+\int_{0}^{i_{1},i_{2}}(Mi_{2}di_{1}+Mi_{1}di_{2})}$$
$$\mathrm{w_{f}=\frac{1}{2}L_{1}i_{1}^2+\frac{1}{2}L_{2}i_{2}^2+Mi_{1}i_{2}\:\:\:\:\:\:...(9)}$$
電磁轉矩
當轉子旋轉時，場能隨時間的變化率由對方程 (9) 求導得到：
$$\mathrm{\frac{d w_{f}}{dt}=\frac{1}{2}L_{1}\frac{d i_{1}^{2}}{dt}+\frac{1}{2}i_{1}^2\frac{dL_{1}}{dt}+\frac{1}{2}L_{2}\frac{d i_{2}^{2}}{dt}+\frac{1}{2}i_{2}^2\frac{dL_{2}}{dt}+i_{1}i_{2}\frac{dM}{dt}+Mi_{1}\frac{di_{2}}{dt}+Mi_{2}\frac{di_{1}}{dt}}$$
$$\mathrm{\Longrightarrow\frac{d w_{f}}{dt}=L_{1}i_{1}\frac{di_{1}}{dt}\frac{1}{2}i_{1}^2\frac{dL_{1}}{dt}+L_{2}i_{2}\frac{di_{2}}{dt}+\frac{1}{2}i_{1}^2\frac{dL_{1}}{dt}+\frac{1}{2}L_{2}\frac{di_{2}^{2}}{dt}+\frac{1}{2}i_{2}^2\frac{dL_{2}}{dt}+i_{1}i_{2}\frac{dM}{dt}+Mi_{1}\frac{di_{2}}{dt}+Mi_{2}\frac{di_{1}}{dt}\:\:\:\:\:\:...(10)}$$
對方程 (10) 關於時間積分，得到：
$$\mathrm{W_{f}=\int L_{1}i_{1}d_{1}+\frac{1}{2}i_{1}^2dL_{1} \int L_{2}i_{2}d_{2}+\frac{1}{2}i_{2}^2dL_{2}+i_{1}i_{2}dM+Mi_{1}di_{2}+Mi_{2}di_{1}\:\:\:\:\:\:...(11)}$$
方程 (11) 是一個運動換能器的通用方程，其中 $L_{1}$、$L_{2}$、$M, i_{1}$ 和 $i_{2} $ 都隨位置和時間變化。現在，將方程 (11) 與方程 (8) 進行比較，得到：
$$\mathrm{W_{m}=\int(\frac{1}{2}i_{1}^2dL_{1}+\frac{1}{2}i_{2}^2dL_{2}+i_{1}i_{2}dM+)\:\:\:\:\:\:...(12)}$$
對方程 (12) 關於轉子角度 $θ_{m}$ 求導，得到：
$$\mathrm{\frac{dW_{m}}{dθ_{m}}=\int(\frac{1}{2}i_{1}^2\frac{dL_{1}}{dθ_{m}}+\frac{1}{2}i_{2}^2\frac{dL_{2}}{dθ_{m}}+i_{1}i_{2}\frac{dM}{dθ_{m}})}$$
$$\mathrm{\Longrightarrow \tau_{e}=\frac{1}{2}i_{1}^2\frac{dL_{1}}{dθ_{m}}+\frac{1}{2}i_{2}^2\frac{dL_{2}}{dθ_{m}}+i_{1}i_{2}\frac{dM}{dθ_{m}}\:\:\:\:\:\:...(13)}$$
方程 (13) 的前兩項是磁阻轉矩，最後一項稱為同軸轉矩，這是由於兩個疊加的磁場試圖對齊而產生的。
重要 - 對於具有均勻氣隙的電機，不會產生磁阻轉矩。
數值示例
對於雙勵系統，電感如下所示：
$$\mathrm{L_{1}=10+2cos2θ;L_{2}=5+2cos2θ;M=20cosθ}$$
線圈由電流 $i_{1}$=0.5A 和 $i_{2}$=0.6A 激勵。
求轉矩作為 θ 的函式。
求儲存在系統中的能量作為 θ 的函式。
解決方案
雙勵系統產生的轉矩由下式給出：
$$\mathrm{\tau_{e}=\frac{1}{2}i_{1}^2\frac{dL_{1}}{dθ_{m}}+\frac{1}{2}i_{2}^2\frac{dL_{2}}{dθ_{m}}+i_{1}i_{2}\frac{dM}{dθ_{m}}}$$
這裡，
$$\mathrm{\frac{dL_{1}}{dθ_{m}}=-4sin2θ;\frac{dL_{2}}{dθ_{m}}=-6sin2θ;=-20sinθ}$$
$$\mathrm{\Longrightarrow\tau_{e}=\frac{1}{2}\times(0.5)^2\times(-4sin2θ)+\frac{1}{2}\times(0.6)^2\times(-6sin2θ)+(0.5)\times(0.6)\times-20sinθ}$$
$$\mathrm{\therefore\tau_=-1.58sin2θ-6sinθNm}$$
儲存在雙勵系統中的能量由下式給出：
$$\mathrm{W_{f}=\frac{1}{2}L_{1}i_{1}^2+\frac{1}{2}L_{2}i_{2}^2+Mi_{1}i_{2}}$$
$$\mathrm{\Longrightarrow W_{f}=\frac{1}{2}(10+2cos2θ)(0.5)^2+\frac{1}{2}(5+2cos3θ)(0.6)^2+(20cosθ)(0.5)(0.6)}$$
$$\mathrm{\Longrightarrow W_{f}=2.15+0.79cos2θ+6cosθ}$$
5K+ 次檢視
