頻率單位

---

介紹

波是在介質中傳播能量而不傳播質量的擾動。波通常以週期性運動的形式存在，例如簡諧振盪器。它們有波峰和波谷。

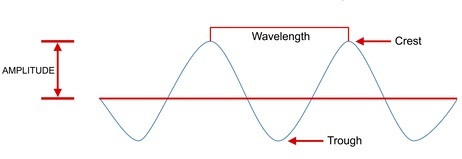
波的振幅是波的高度。兩個連續波峰之間所覆蓋的距離稱為波長。每秒透過的波數稱為波的頻率。相位不是波的屬性。但它給出了兩個具有相同頻率的訊號之間的關係。

現在，我們將討論波、低頻波和高頻波及其單位。

什麼是頻率？

在特定時間內透過某一點的波數稱為頻率。它也表示為每單位時間的振動次數或迴圈次數。如果一個物體處於週期性運動中，它會完成一個完整的事件並返回到其原始位置。波的頻率是完成一個迴圈所需時間間隔的倒數。

音叉的叉臂以特定的頻率來回振動。頻率通常與振動、振盪和旋轉等過程相關。頻率用 f 表示。頻率是音訊訊號、機械振動、光和無線電波中的一個重要因素。

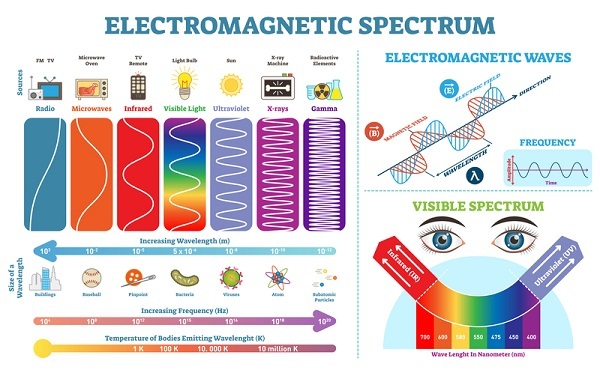
頻率單位

頻率的單位是赫茲。每秒一次振動或振盪表示為一赫茲。透過空氣傳播的聲波會使氣壓發生變化。這種氣壓會被人類和生物的耳朵檢測到，從而捕捉到聲音。通常，人類可聽到的聲波頻率範圍在 20Hz 到 20000 Hz 之間。

次聲波的頻率低於人類可聽範圍的頻率。即小於 20 Hz。超聲波的頻率高於人類可聽範圍的頻率。即大於 20000 Hz。由頻率引起的感知稱為音調。如果聲波的頻率高，則音調也高，反之亦然。

$$\mathrm{1\:赫茲=1\:振動\:秒^{−1}}$$

一千赫茲等於 1000 赫茲，1 兆赫茲等於 106 赫茲，1 吉赫茲等於 10⁹ 赫茲。在光譜學中，頻率以波數來測量。每單位距離的波數稱為波數。在機械裝置中，它計算為每分鐘轉數 (rpm)。

$$\mathrm{1\:赫茲 = 60\:rpm}$$

根據粒子的週期性運動，頻率分為兩種。它們是空間頻率和角頻率。

空間頻率

粒子的空間頻率受空間座標控制。空間頻率是任何週期性結構的特徵。粒子的空間頻率與振動粒子的波長成反比。空間輻射的測量以米/弧度為單位。

角頻率

進行旋轉運動的粒子與角頻率相關。它由粒子在特定時間內完成的旋轉次數定義。角頻率的單位也是赫茲。角頻率用 $\mathrm{\omega}$ 表示。頻率和角頻率表示為：

$$\mathrm{f=\frac{\omega}{2\pi}}$$

$\mathrm{\omega}$ 表示粒子的角頻率。

因此，角頻率由下式給出：

$$\mathrm{\omega=2\pi f}$$

頻率公式

根據已知量，計算頻率的公式分為三種。

公式-1

粒子的頻率是粒子振盪週期的倒數，表示為

$$\mathrm{f=\frac{1}{T}}$$

這裡 f 表示粒子的頻率。

這裡 T 表示粒子完成一個迴圈所需的時間。

公式-2

頻率也指波的速度與波長的比率，表示為：

$$\mathrm{f=\frac{速度}{波長}}$$

$$\mathrm{f=\frac{
u}{\lambda}}$$

這裡 v 表示波的速度

這裡 $\mathrm{\lambda}$ 表示波長。

公式-3

頻率也可以透過進行旋轉運動的粒子的角速度來計算，表示為：

$$\mathrm{f=\frac{\omega}{2\pi}}$$

例題

1. 波長為 400 nm 的光波的頻率是多少？

已知

$$\mathrm{波長= \lambda=400 \times 10^{−9}m}$$

$$\mathrm{光速\:c=3 \times 10^{8}\: m/s}$$

光波的頻率 $\mathrm{= f=\frac{c}{\lambda}}$

$$\mathrm{f=\frac{3 \times 10^{8}}{400 \times 10^{−9}}}$$

$$\mathrm{f=\frac{3}{400}\times 10^{8}\times 10^{9}}$$

$$\mathrm{f=0.75\times 10^{−2}\times 10^{8}\times 10^{9}}$$

$$\mathrm{f=0.75 \times 10^{15}}$$

$$\mathrm{f=7.5 \times 10^{14}\:Hz}$$

因此，光波的頻率為 $\mathrm{f=7.5\times\:10^{14}\:Hz}$

2. 計算一個擺完成一個迴圈需要 5 秒的頻率。

已知：所需時間 = T =5 秒

擺的頻率為 $\mathrm{f=\frac{1}{T}}$

$$\mathrm{f=\frac{1}{5}}$$

$$\mathrm{f=0.2\:Hz}$$

擺的頻率為 0.2 Hz。

結論

在本教程中，討論了關於頻率、頻率單位和角頻率的事實。還討論了頻率公式和一些例題。

常見問題

Q1. 什麼是頻率調製？

答：如果瞬時訊號電壓發生變化，則載波頻率會發生變化。這稱為頻率調製。因此，載波的幅度和相位不會發生變化。

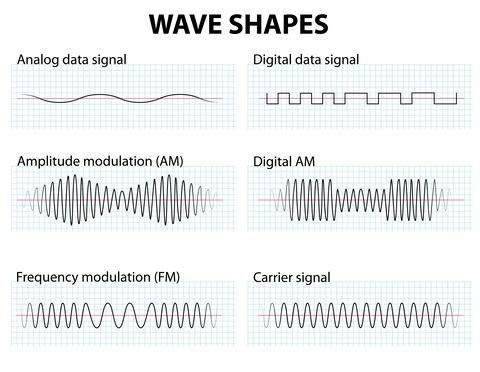
Q2. 給出 FM 調製的應用

答：頻率調製應用於雷達和腦電圖監測電路。它主要用於 FM 廣播。它也應用於磁帶錄音系統。它在衛星和微波通訊、蜂窩無線通訊和電視聲音傳輸中具有廣泛的應用。

Q3. 頻率調製的應用有哪些？

答：頻率調製用於研究振盪現象、音訊波、無線電波和光波的振動現象。頻率公式用於測量波長、頻率、波速、週期和一些其他相關公式。

Q4. 幅度調製和頻率調製有什麼區別？

答：

幅度調製	頻率調製
根據載波訊號變化幅度	根據載波訊號變化頻率
頻率和相位保持恆定	幅度和相位保持恆定
音質差	音質好
與 FM 相比，它不太複雜	它更復雜。
頻寬較小	頻寬較大
傳輸過程中浪費功率	它效率很高，因為所有功率都得到了利用。

Q5. 如何測量頻率？

答：有兩種型別的儀器用於測量頻率，例如轉速錶和振盪器。Fullarton 轉速錶和 Frahm 轉速錶是用於測量頻率的轉速錶型別。石英振盪器、銣振盪器和銫振盪器是振盪器型別。在普通的電路中，頻率由數字萬用表、功率分析儀和示波器測量。