資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學晶胞密度
引言
晶胞的質量與晶胞體積之比稱為晶胞密度。晶胞的質量等於晶胞中原子個數乘以每個原子的質量。
晶胞是固體中最緊湊且最基本的重複結構單元，用於表示固體的晶體結構。這種視覺化也有助於計算晶胞密度。晶胞重複形成網路，稱為晶格，晶格中的粒子在空間中表示為點。晶胞有多種形狀，取決於邊角之間的角度和邊長。固體的整體對稱性取決於晶胞的型別。通過了解晶胞的晶格結構，可以輕鬆計算晶胞密度。
什麼是晶胞？
固體的結構是三維排列的，它們的排列具有重複單元。因此，每個固體結構單元中最小的重複單元稱為晶胞。晶胞的重複形成晶體。根據排列型別，晶胞有多種型別。主要晶胞和非主要晶胞是兩大類。
當構成粒子僅位於角頂時，稱為簡單晶胞（或稱原始晶胞）。如果構成粒子既位於角頂又在其他位置，則為非主要晶胞。晶胞有六個引數：三個角之間的角度 (α、β 和 γ) 和三個邊長 (a、b 和 c)。
視覺化的益處
固體晶體結構的視覺化非常重要。它可以用來解釋：
固體的性質。
幫助識別堆垛方式。
幫助識別擴充套件結構。
瞭解固體的離子晶格。
給出固體的實驗式。
從視覺化中獲得單個晶胞的知識。
什麼是晶格？
固體中原子或離子的三維空間排列稱為晶格。為了降低總的分子間能量，固體中的原子以某種幾何形狀排列，這就是固體的晶格結構。因此，它是一種示意圖表示，包括原子、離子和分子。構成粒子用點表示，稱為晶格點。透過直線連線這些點形成晶格的幾何形狀。
布拉維晶格
如果在晶格中，周圍的晶格點都相同，或者所有粒子都相同，則稱為布拉維晶格。在這樣的晶體中，原子的排列方向也相同。1848年，布拉維指出，描述晶體只需要14種晶格，這就是布拉維晶格。根據布拉維晶格的晶胞引數，共有7種晶系，它們是：
三方晶系（或菱方晶系）
四方晶系
三斜晶系
單斜晶系
立方晶系
六方晶系
正交晶系
晶胞密度計算
晶胞密度是晶胞質量與晶胞體積之比。我們可以用以下公式簡單地計算它。
$$\mathrm{密度,\rho\:=\:質量\: / \:體積}$$
晶胞質量可以用以下公式計算：
$\mathrm{晶胞質量\:=\:晶胞中原子個數\:\times\:每個原子的質量\:}$
$$\mathrm{m\:=\:M/N_{A},\:其中\:M\:=\:摩爾質量}$$
體積可以透過晶胞的邊長計算得出。如果a是邊長，則體積是：
$$\mathrm{V\:=\:a^{3}}$$
$\mathrm{所以,\:密度,\:\rho\:=\:z\:\times\:m/a^{3}\:=\:\frac{z\:\times\:M}{N_{A}a^{3}}}$
示例
一種具有體心立方晶體結構的化合物，原子質量為50 amu，邊長為290 pm。計算晶胞的密度（單位為gcm⁻³）。
答案：計算密度的公式為$\mathrm{\rho\:=\:z\:\times\:m/a^{3}\:=\:\frac{z\:\times\:M}{N_{A}a^{3}}}$
體心立方的原子數為2(z)。
$$\mathrm{\rho\:=\:\frac{2\:\times\:50}{6.022\:\times\:10^{23}\:\times\:(290\:\times\:10^{-10})^{3}}\:=\:6.81\:gcm^{-3}}$$
因此，密度為$\mathrm{6.81\:gcm^{-3}}$
該技術的意義
晶胞密度計算公式具有一定的意義，例如：
當已知其他所有因素時，可用於計算邊長。
如果已知密度，也可用於計算晶胞的體積。
也可用於計算晶胞的質量。
可用於計算多種晶體的密度。
各種情況下晶胞密度的一般表示式
計算晶胞密度的一般公式為：
$$\mathrm{\rho\:=\:z\:\times\:m/a^{3}}$$
面心立方（FCC）晶胞中(110)平面的平面密度是多少？
單位面積上原子的數量是平面密度。FCC 110的平面密度為：
$\mathrm{\:\:\:\:\:平面密度\:=\:\frac{原子數}{平面面積}}$
$\mathrm{\:\:\:\:\:\:\:\:=\:0.177/\:(構成粒子的半徑)^{2}}$
已知構成原子的半徑，就可以計算平面密度。
簡單晶胞
當構成粒子僅存在於晶格點（即立方體的8個頂點）時，稱為簡單晶胞。因此，它只包含一個晶格點。它是所有其他晶體結構的基本晶胞，因為在這個晶胞上新增一些原子會導致其他晶胞的形成。
體心立方晶胞
這是非主要晶胞的一種分類。立方體的八個角上都有原子，中間還有一個原子，從而構成體心立方晶胞。體心立方晶胞的配位數為8。原子總數為2，中心一個，八個角各一個。
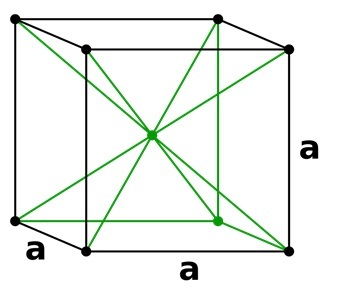
Mih.s29 , 體心立方晶格 , CC BY-SA 4.0
面心立方晶胞
這也是一種非主要晶胞。在這種晶胞中，立方結構的八個角上各有一個原子，每個面的中心也各有一個原子。這種晶胞的配位數為12。原子總數為4。
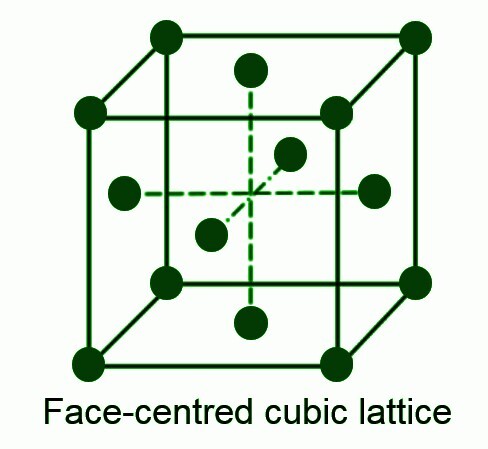
關於晶胞
就像生物體由細胞構成一樣，我們周圍的所有晶體都由稱為晶胞的最小的重複單元構成。因此，它是每種晶體的基本組成部分。晶胞也代表結構的對稱性。它們以適當的方式排列，以獲得每種晶體的完美形狀。
晶格常數和密度之間關係的解釋
晶格常數是所有晶格的引數。邊長a、b和c是引數。它與密度計算的關係如下式所示：
$$\mathrm{\rho\:=\:z\:\times\:m/(晶格常數)^{3}}$$
金剛石晶體結構
金剛石是一種具有面心立方布拉維晶格的立方結構，由碳元素構成。因此，立方結構的八個角上和所有面的中心各有一個原子。因此，原子總數為4。因此，金剛石包含面心立方晶格的重複單元。
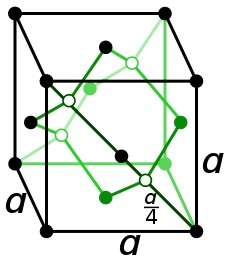
結論
晶胞是每種晶體中最小的重複單元。晶胞賦予晶體對稱性和形狀。原子的三維排列導致晶格的形成。晶胞有兩種型別：主要晶胞和非主要晶胞。晶胞有六個引數：三個角度和三個邊長。每種晶胞的密度都用公式ρ = z × m/a³計算。晶格常數a與密度計算有關。共有七種晶系，稱為布拉維晶格。金剛石的立方結構是面心立方晶格。
常見問題
1. 什麼是底心晶胞？
這是一種非主要晶胞，其中粒子存在於8個角上和兩個相對面的中心。因此，原子總數為2。
2. NaCl是體心立方結構嗎？
NaCl是面心立方結構，包含四個鈉原子和四個氯原子。
3. hcp的例子是什麼？
許多元素金屬具有hcp（六方密堆積）結構。例如，鈦、鋅等。
4. 什麼是簡單立方晶格？
簡單立方晶格是最簡單的晶胞。它只包含立方體角上的原子。因此，它也稱為簡單立方。
5. 金金屬是簡單立方晶胞嗎？
金金屬是面心立方晶格。所有金原子都排列為面心立方（FCC）晶格的重複單元。
瀏覽量：229
