轉動慣量的單位

---

介紹

物體的質量與其到旋轉軸距離平方的乘積決定了它的轉動慣量。以質心 (COM) 為例，轉動慣量是從質心概念發展而來的概念。質心代表物體中所有質量都集中在一個假想點上。當物體具有慣性時，它自身無法改變其位置或運動的均勻性。由於改變質量更大的物體的狀態需要更多的能量，因此它具有更大的慣性。

轉動慣量

它是物體對旋轉變化的阻力大小。它需要根據不同的旋轉軸來定義。關於給定旋轉軸的轉動慣量是物體旋轉慣性的量度。它量化了物體的各個部分如何在距軸的不同間隔處進行劃分。

剛體的轉動慣量由以下因素決定

• 體重指數、形狀、大小。

• 物體尺寸和形狀。

• 質量圍繞旋轉軸的分佈。

任何實體都有一個形心或重心，即物體內部重力似乎作用的點。如果一個靜止的物體的重心位於透過它的垂直線上，那麼它將保持靜止。二維表面的形心對應於該面積的重心。

垂直軸定理

在平面區域中，轉動慣量 (M. O. I.) 等於圍繞相互垂直軸的轉動慣量的總和。

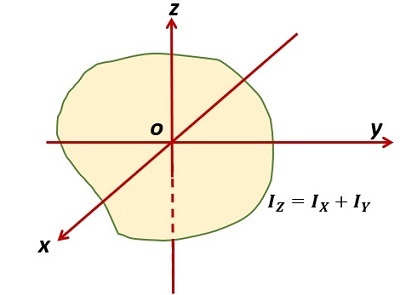
也就是說，轉動慣量是

$$\mathrm{I_Z=I_X+I_Y}$$

平行軸定理

平行於形心軸的軸上的轉動慣量等於形心軸上的轉動慣量加上物體的質量乘以參考軸距離的平方。

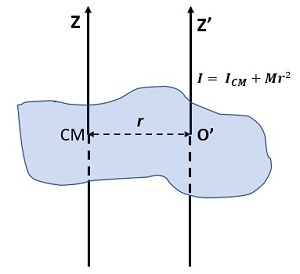
$$\mathrm{I= I_{CM}+Mr^2}$$

這裡，平行於形心軸的軸上的轉動慣量 = I

形心軸上的轉動慣量 = $\mathrm{I_{CM}}$

兩個形心軸之間的垂直距離 = $\mathrm{r}$

透過將力乘以點與作用線的垂直距離，我們可以計算作用於點的力矩。

在每個物體中，都存在一個點，可以假設物體的整個質量都集中在這個點上。這個質量點的徑向距離和旋轉軸稱為回轉半徑 (K)。可以使用以下公式根據回轉半徑計算轉動慣量。

$$\mathrm{I=MK^2}$$

這裡，轉動慣量 = $\mathrm{I}$

物體的質量 = $\mathrm{M}$

回轉半徑 = $\mathrm{K}$

剛體的轉動慣量

慣性

當物體具有慣性時，它自身無法改變其位置或運動的均勻性。質量更大的物體具有更大的慣性，因為改變其狀態需要更大的力。物體的慣性是根據其質量計算的。

旋轉慣性

旋轉慣性是可以在軸上旋轉的物體的屬性。物體的旋轉慣性隨著改變其旋轉狀態所需的扭矩或力偶而增加。物體的旋轉慣性表示為物體繞旋轉軸的轉動慣量。隨著旋轉軸的變化，旋轉慣性也會發生變化。

影響轉動慣量的因素

物體的質量與其到旋轉軸距離平方的乘積決定了它的轉動慣量。轉動慣量是從質心概念發展而來的概念。轉動慣量是指物體對旋轉變化的抵抗程度。它必須根據特定的旋轉軸來定義。物體的旋轉慣性由繞特定旋轉軸的轉動慣量來衡量。它衡量了物體如何在距軸的不同距離處被分成不同的部分。

粒子的轉動慣量公式為

$$\mathrm{I=mr^2}$$

物體的轉動慣量由以下因素決定 -

• 體重指數。

• 物體尺寸和形狀

• 質量圍繞旋轉軸的分佈

• 旋轉軸相對於物體的對齊和放置。

轉動慣量的單位

物體的轉動慣量 (M. O. I.) 公式為

$$\mathrm{I=mr^2}$$

質量單位為 kg，長度單位為米。

轉動慣量的單位將為 $\mathrm{kg.m^2}$。

結論

轉動慣量是從質心概念發展而來的概念。質心是物體中所有質量都集中在一個假想點上。物體的質量與其到旋轉軸距離平方的乘積決定了它的轉動慣量。

當物體具有轉動慣量時，它自身無法改變其位置或旋轉運動的均勻性。質量更大的物體具有更大的轉動慣量，因為改變其旋轉狀態需要更大的力矩。轉動慣量 (M. O. I.) 的單位為 $\mathrm{kg.m^2}$。旋轉軸的位置和質量的分佈決定了剛性粒子的轉動慣量。

常見問題

Q1. 力作用點的軌跡是否會影響轉動慣量？

A. 不會。力的作用點的大小、方向和軌跡決定了力矩。轉動慣量受質量及其相對於旋轉軸的分佈的影響

Q2. 為什麼轉動慣量保持不變？

A. 不會，物體質量元素的轉動慣量之和構成了物體的總轉動慣量。與任何給定物體的質量恆定相反，轉動慣量受旋轉中心位置的影響。通常使用積分微積分來計算轉動慣量。

Q3. 所有物體中都存在慣性嗎？

A. 作為一種力，慣性阻止靜止的物體運動並保持運動的物體以恆定的速度運動，它是一種阻止所有物體停止的力。所有物體中都存在慣性。質量較大的物體的慣性大於相當小的物體的慣性。

Q4. 如果轉動慣量增加會發生什麼？

A. 物體的轉動慣量越大，改變其旋轉狀態所需的力就越大。隨著轉動慣量的增加，物體對其旋轉狀態變化的抵抗力也會增加。