Python - 分治法

在分治法中，手頭的問題被分解成更小的子問題，然後每個子問題都獨立解決。當我們繼續將子問題分解成更小的子問題時，我們最終可能會達到無法再進行分解的階段。這些“原子”級的最小可能子問題（部分）得到解決。最後，將所有子問題的解決方案合併起來，以獲得原始問題的解決方案。

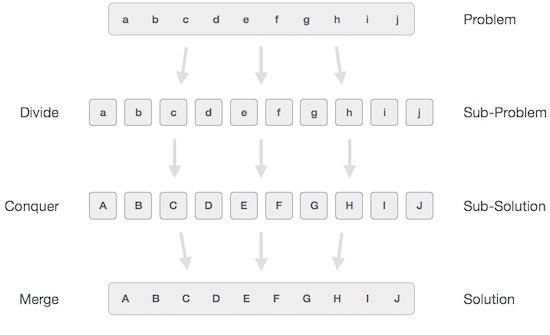
總的來說，我們可以將分治法理解為一個三步過程。

分解/分割

此步驟涉及將問題分解成更小的子問題。子問題應代表原始問題的一部分。此步驟通常採用遞迴方法來分解問題，直到沒有子問題可以進一步分解。在此階段，子問題變得具有原子性，但仍然代表實際問題的一部分。

解決/征服

此步驟接收許多需要解決的較小子問題。通常，在此級別，問題被認為是“獨立解決”的。

合併/組合

當較小子問題得到解決後，此階段遞迴地將它們組合起來，直到它們形成原始問題的解決方案。這種演算法方法以遞迴方式工作，並且解決和合並步驟非常接近，以至於它們看起來像一個步驟。

示例

以下程式是分治法程式設計方法的一個示例，其中使用 Python 實現二分查詢。

二分查詢實現

在二分查詢中，我們取一個排序好的元素列表，並開始在列表中間查詢元素。如果搜尋值與列表中的中間值匹配，則我們完成搜尋。否則，我們透過選擇繼續處理列表的右側或左側一半來消除一半的元素列表，具體取決於搜尋項的值。

這是可能的，因為列表已排序，並且它比線性搜尋快得多。在這裡，我們劃分給定的列表並透過選擇列表的適當一半來征服。我們重複這種方法，直到找到該元素或得出關於它在列表中不存在的結論。

示例

def bsearch(list, val):
   list_size = len(list) - 1
   idx0 = 0
   idxn = list_size
# Find the middle most value
   while idx0 <= idxn:
      midval = (idx0 + idxn)// 2
      if list[midval] == val:
         return midval
# Compare the value the middle most value
   if val > list[midval]:
      idx0 = midval + 1
   else:
      idxn = midval - 1
   if idx0 > idxn:
      return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

輸出

執行上述程式碼時，會產生以下結果：

5
None