
- Python 資料結構和演算法教程
- Python - 資料結構首頁
- Python - 資料結構簡介
- Python - 資料結構環境
- Python - 陣列
- Python - 列表
- Python - 元組
- Python - 字典
- Python - 二維陣列
- Python - 矩陣
- Python - 集合
- Python - 對映
- Python - 連結串列
- Python - 棧
- Python - 佇列
- Python - 雙端佇列
- Python - 高階連結串列
- Python - 雜湊表
- Python - 二叉樹
- Python - 搜尋樹
- Python - 堆
- Python - 圖
- Python - 演算法設計
- Python - 分治法
- Python - 遞迴
- Python - 回溯法
- Python - 排序演算法
- Python - 搜尋演算法
- Python - 圖演算法
- Python - 演算法分析
- Python - 大O表示法
- Python - 演算法類
- Python - 均攤分析
- Python - 演算法論證
- Python 資料結構與演算法有用資源
- Python - 快速指南
- Python - 有用資源
- Python - 討論
Python - 演算法型別
為了比較演算法併為特定場景選擇特定演算法,必須分析演算法的效率和準確性。進行此分析的過程稱為漸近分析。它指的是用數學計算單位計算任何操作的執行時間。
例如,一個操作的執行時間計算為 f(n),而另一個操作的執行時間計算為 g(n2)。這意味著第一個操作的執行時間將隨著 n 的增加而線性增加,而第二個操作的執行時間將隨著 n 的增加而呈指數增長。同樣,如果 n 非常小,則兩個操作的執行時間幾乎相同。
通常,演算法所需的時間分為三種類型:
最佳情況 - 程式執行所需的最小時間。
平均情況 - 程式執行所需的平均時間。
最壞情況 - 程式執行所需的最多時間。
漸近記號
常用的漸近記號來計算演算法的執行時間複雜度。
Ο 記號
Ω 記號
θ 記號
大O記號,Ο
Ο(n) 表示法是表達演算法執行時間上限的正式方式。它衡量最壞情況時間複雜度或演算法可能完成所需的最長時間。

例如,對於函式 f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
Ω 記號,Ω
Ω(n) 表示法是表達演算法執行時間下限的正式方式。它衡量最佳情況時間複雜度或演算法可能完成所需的最短時間。
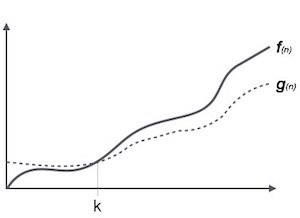
例如,對於函式 f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
θ 記號,θ
θ(n) 表示法是表達演算法執行時間下限和上限的正式方式。它表示如下:
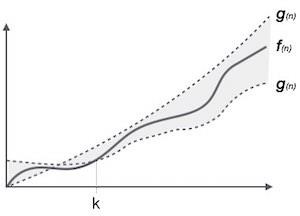
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
常見漸近記號
下面列出了一些常見的漸近記號:
| 常數 | — | Ο(1) |
| 對數 | — | Ο(log n) |
| 線性 | — | Ο(n) |
| n log n | — | Ο(n log n) |
| 平方 | — | Ο(n2) |
| 立方 | — | Ο(n3) |
| 多項式 | — | nΟ(1) |
| 指數 | — | 2Ο(n) |
廣告