
- Python 資料結構與演算法教程
- Python - DS 首頁
- Python - DS 簡介
- Python - DS 環境
- Python - 陣列
- Python - 列表
- Python - 元組
- Python - 字典
- Python - 二維陣列
- Python - 矩陣
- Python - 集合
- Python - 對映
- Python - 連結串列
- Python - 棧
- Python - 佇列
- Python - 雙端佇列
- Python - 高階連結串列
- Python - 雜湊表
- Python - 二叉樹
- Python - 搜尋樹
- Python - 堆
- Python - 圖
- Python - 演算法設計
- Python - 分治法
- Python - 遞迴
- Python - 回溯法
- Python - 排序演算法
- Python - 搜尋演算法
- Python - 圖演算法
- Python - 演算法分析
- Python - 大O表示法
- Python - 演算法類別
- Python - 均攤分析
- Python - 演算法論證
- Python 資料結構與演算法實用資源
- Python - 快速指南
- Python - 實用資源
- Python - 討論
Python 資料結構 - 快速指南
Python - DS 簡介
在這裡,我們將瞭解在 Python 程式語言中什麼是資料結構。
資料結構概述
資料結構是計算機科學的基本概念,有助於用任何語言編寫高效的程式。Python 是一種高階的、解釋型的、互動式的和麵向物件的指令碼語言,使用它我們可以比其他程式語言更簡單地學習資料結構的基礎知識。
在本章中,我們將簡要概述一些常用的通用資料結構,以及它們與某些特定的 Python 資料型別之間的關係。還有一些特定於 Python 的資料結構,它們被列為另一類。
通用資料結構
計算機科學中的各種資料結構大致分為以下兩類。我們將在後續章節中詳細討論每種資料結構。
線性資料結構
這些是按順序儲存資料元素的資料結構。
陣列 - 它是由資料元素及其索引配對組成的順序排列。
連結串列 - 每個資料元素除了包含資料外,還包含指向另一個元素的連結。
棧 - 它是一種只遵循特定操作順序的資料結構。後進先出 (LIFO) 或先進後出 (FILO)。
佇列 - 它類似於棧,但操作順序僅為先進先出 (FIFO)。
矩陣 - 它是一種二維資料結構,其中資料元素由一對索引引用。
非線性資料結構
這些是資料元素之間沒有順序連結的資料結構。任何一對或一組資料元素都可以相互連結,並且可以無需嚴格的順序訪問。
二叉樹 - 它是一種資料結構,其中每個資料元素最多可以連線到另外兩個資料元素,並且它以根節點開始。
堆 - 它是樹資料結構的一種特殊情況,其中父節點中的資料要麼嚴格大於/等於子節點,要麼嚴格小於子節點。
雜湊表 - 它是由使用雜湊函式相互關聯的陣列組成的資料結構。它使用鍵而不是資料元素的索引來檢索值。
圖 - 它是由頂點和節點組成的排列,其中某些節點透過連結相互連線。
Python 特定資料結構
這些資料結構特定於 Python 語言,它們在儲存不同型別的資料和在 Python 環境中進行更快的處理方面提供了更大的靈活性。
列表 - 它類似於陣列,但資料元素可以是不同資料型別。您可以在 Python 列表中同時擁有數字和字串資料。
元組 - 元組類似於列表,但它們是不可變的,這意味著元組中的值不能修改,只能讀取。
字典 - 字典包含鍵值對作為其資料元素。
在接下來的章節中,我們將學習如何使用 Python 實現每個資料結構的詳細資訊。
Python - DS 環境
Python 可用於各種平臺,包括 Linux 和 Mac OS X。讓我們瞭解如何設定我們的 Python 環境。
本地環境設定
開啟一個終端視窗,然後鍵入“python”以檢視它是否已安裝以及安裝了哪個版本。
- Unix(Solaris、Linux、FreeBSD、AIX、HP/UX、SunOS、IRIX 等)
- Win 9x/NT/2000
- Macintosh(Intel、PPC、68K)
- OS/2
- DOS(多個版本)
- PalmOS
- 諾基亞手機
- Windows CE
- Acorn/RISC OS
- BeOS
- Amiga
- VMS/OpenVMS
- QNX
- VxWorks
- Psion
- Python 也已移植到 Java 和 .NET 虛擬機器
獲取 Python
最新的原始碼、二進位制檔案、文件、新聞等都可以在 Python 的官方網站上找到 www.python.org
您可以從此處提供的網站下載 Python 文件,www.python.org/doc。該文件以 HTML、PDF 和 PostScript 格式提供。
安裝 Python
Python 發行版適用於各種平臺。您只需要下載適用於您平臺的二進位制程式碼並安裝 Python。
如果您的平臺沒有提供二進位制程式碼,則需要一個 C 編譯器來手動編譯原始碼。編譯原始碼在您所需的安裝功能方面提供了更大的靈活性。
以下是關於在各種平臺上安裝 Python 的快速概述 -
Unix 和 Linux 安裝
以下是在 Unix/Linux 機器上安裝 Python 的簡單步驟。
開啟 Web 瀏覽器並轉到 www.python.org/downloads。
點選連結下載適用於 Unix/Linux 的壓縮原始碼。
下載並解壓縮檔案。
如果您想自定義某些選項,請編輯Modules/Setup 檔案。
執行 ./configure 指令碼
make
make install
這會將 Python 安裝到標準位置/usr/local/bin,並將庫安裝到/usr/local/lib/pythonXX,其中 XX 是 Python 的版本。
Windows 安裝
以下是在 Windows 機器上安裝 Python 的步驟。
開啟 Web 瀏覽器並轉到 www.python.org/downloads。
點選 Windows 安裝程式python-XYZ.msi 檔案的連結,其中 XYZ 是您需要安裝的版本。
要使用此安裝程式python-XYZ.msi,Windows 系統必須支援 Microsoft Installer 2.0。將安裝程式檔案儲存到您的本地機器,然後執行它以檢視您的機器是否支援 MSI。
執行下載的檔案。這將開啟 Python 安裝嚮導,該向導非常易於使用。只需接受預設設定,等待安裝完成,即可完成。
Macintosh 安裝
最近的 Mac 都已安裝了 Python,但它可能已經過時幾年了。請參閱 www.python.org/download/mac/,瞭解有關獲取最新版本以及支援在 Mac 上進行開發的其他工具的說明。對於 Mac OS X 10.3(2003 年釋出)之前的舊版 Mac OS,可以使用 MacPython。
Jack Jansen 維護它,您可以在他的網站上完全訪問所有文件 - http://www.cwi.nl/~jack/macpython.html。您可以在其中找到 Mac OS 安裝的完整安裝詳細資訊。
設定 PATH
程式和其他可執行檔案可能位於許多目錄中,因此作業系統提供了一個搜尋路徑,該路徑列出了作業系統搜尋可執行檔案的目錄。
該路徑儲存在環境變數中,環境變數是作業系統維護的命名字串。此變數包含命令 shell 和其他程式可用的資訊。
路徑變數在 Unix 中命名為 PATH,在 Windows 中命名為 Path(Unix 區分大小寫;Windows 不區分)。
在 Mac OS 中,安裝程式會處理路徑詳細資訊。要從任何特定目錄呼叫 Python 直譯器,您必須將 Python 目錄新增到您的路徑中。
在 Unix/Linux 上設定路徑
要在 Unix 中為特定會話將 Python 目錄新增到路徑中 -
在 csh shell 中 - 鍵入 setenv PATH "$PATH:/usr/local/bin/python" 並按 Enter。
在 bash shell(Linux)中 - 鍵入 export ATH="$PATH:/usr/local/bin/python" 並按 Enter。
在 sh 或 ksh shell 中 - 鍵入 PATH="$PATH:/usr/local/bin/python" 並按 Enter。
注意 - /usr/local/bin/python 是 Python 目錄的路徑
在 Windows 上設定路徑
要在 Windows 中為特定會話將 Python 目錄新增到路徑中 -
在命令提示符下 - 鍵入 path %path%;C:\Python 並按 Enter。
注意 - C:\Python 是 Python 目錄的路徑
Python 環境變數
以下是 Python 可以識別的重要環境變數 -
| 序號 | 變數和描述 |
|---|---|
| 1 |
PYTHONPATH 它與 PATH 的作用類似。此變數告訴 Python 直譯器在哪裡查詢匯入到程式中的模組檔案。它應包含 Python 源庫目錄和包含 Python 原始碼的目錄。PYTHONPATH 有時由 Python 安裝程式預設。 |
| 2 |
PYTHONSTARTUP 它包含一個初始化檔案的路徑,該檔案包含 Python 原始碼。每次啟動直譯器時都會執行它。在 Unix 中它被命名為.pythonrc.py,並且包含載入實用程式或修改 PYTHONPATH 的命令。 |
| 3 |
PYTHONCASEOK 它用於 Windows,指示 Python 在 import 語句中查詢第一個不區分大小寫的匹配項。將此變數設定為任何值以啟用它。 |
| 4 |
PYTHONHOME 它是一個備用的模組搜尋路徑。它通常嵌入在 PYTHONSTARTUP 或 PYTHONPATH 目錄中,以便輕鬆切換模組庫。 |
執行 Python
有三種不同的方法可以啟動 Python,如下所示:
互動式直譯器
您可以從 Unix、DOS 或任何其他提供命令列直譯器或 shell 視窗的系統啟動 Python。
在命令列中輸入python。
立即在互動式直譯器中開始編碼。
$python # Unix/Linux or python% # Unix/Linux or C:> python # Windows/DOS
以下是所有可用命令列選項的列表,如下所示:
| 序號 | 選項 & 說明 |
|---|---|
| 1 |
-d 它提供除錯輸出。 |
| 2 |
-O 它生成最佳化的位元組碼(生成 .pyo 檔案)。 |
| 3 |
-S 在啟動時不要執行 import site 來查詢 Python 路徑。 |
| 4 |
-v 詳細輸出(import 語句的詳細跟蹤)。 |
| 5 |
-X 停用基於類的內建異常(只使用字串);從版本 1.6 開始已過時。 |
| 6 |
-c cmd 執行作為 cmd 字串傳送的 Python 指令碼 |
| 7 |
file 從給定檔案執行 Python 指令碼 |
來自命令列的指令碼
可以透過在您的應用程式上呼叫直譯器來在命令列中執行 Python 指令碼,如下所示:
$python script.py # Unix/Linux or python% script.py # Unix/Linux or C: >python script.py # Windows/DOS
注意 - 請確保檔案許可權模式允許執行。
整合開發環境(IDE)
如果您系統上有一個支援 Python 的 GUI 應用程式,您也可以從圖形使用者介面 (GUI) 環境執行 Python。
Unix - IDLE 是第一個用於 Python 的 Unix IDE。
Windows - PythonWin 是第一個用於 Python 的 Windows 介面,並且是一個帶有 GUI 的 IDE。
Macintosh - Macintosh 版本的 Python 以及 IDLE IDE 可從主網站獲得,可以下載為 MacBinary 或 BinHex'd 檔案。
如果您無法正確設定環境,則可以向系統管理員尋求幫助。確保 Python 環境已正確設定並正常工作。
注意 - 後續章節中給出的所有示例均使用 CentOS 版本的 Linux 上可用的 Python 2.4.3 版本執行。
我們已經在網上設定了 Python 程式設計環境,以便您可以在學習理論的同時線上執行所有可用示例。隨意修改任何示例並在網上執行它。
Python - 陣列
陣列是一個容器,它可以容納固定數量的項,並且這些項的型別必須相同。大多數資料結構都使用陣列來實現其演算法。以下是理解陣列概念的重要術語:
元素 - 儲存在陣列中的每個專案稱為元素。
索引 - 陣列中每個元素的位置都有一個數字索引,用於識別該元素。
陣列表示
可以在不同語言中以各種方式宣告陣列。下面是一個示例。


根據上圖,以下是要考慮的重要事項:
索引從 0 開始。
陣列長度為 10,這意味著它可以儲存 10 個元素。
每個元素都可以透過其索引訪問。例如,我們可以獲取索引為 6 的元素,即 9。
基本操作
陣列支援的基本操作如下所示:
遍歷 - 一次列印所有陣列元素。
插入 - 在給定索引處新增一個元素。
刪除 - 刪除給定索引處的元素。
搜尋 - 使用給定索引或值搜尋元素。
更新 - 更新給定索引處的元素。
在 Python 中,透過將 array 模組匯入到 Python 程式中來建立陣列。然後,宣告陣列如下所示:
from array import * arrayName = array(typecode, [Initializers])
Typecode 是用於定義陣列將儲存的值型別的程式碼。一些常用的 typecode 如下所示:
| Typecode | 值 |
|---|---|
| b | 表示大小為 1 位元組的有符號整數 |
| B | 表示大小為 1 位元組的無符號整數 |
| c | 表示大小為 1 位元組的字元 |
| i | 表示大小為 2 位元組的有符號整數 |
| I | 表示大小為 2 位元組的無符號整數 |
| f | 表示大小為 4 位元組的浮點數 |
| d | 表示大小為 8 位元組的浮點數 |
在檢視各種陣列操作之前,讓我們使用 python 建立並列印一個數組。
示例
以下程式碼建立了一個名為array1的陣列。
from array import *
array1 = array('i', [10,20,30,40,50])
for x in array1:
print(x)
輸出
當我們編譯並執行上述程式時,它會產生以下結果:
10 20 30 40 50
訪問陣列元素
我們可以使用元素的索引訪問陣列的每個元素。以下程式碼顯示瞭如何訪問陣列元素。
示例
from array import *
array1 = array('i', [10,20,30,40,50])
print (array1[0])
print (array1[2])
輸出
當我們編譯並執行上述程式時,它會產生以下結果,該結果顯示元素已插入索引位置 1。
10 30
插入操作
插入操作是指將一個或多個數據元素插入陣列。根據需求,可以在陣列的開頭、結尾或任何給定索引處新增新元素。
示例
在這裡,我們使用 python 內建的 insert() 方法在陣列中間新增一個數據元素。
from array import *
array1 = array('i', [10,20,30,40,50])
array1.insert(1,60)
for x in array1:
print(x)
當我們編譯並執行上述程式時,它會產生以下結果,該結果顯示元素已插入索引位置 1。
輸出
10 60 20 30 40 50
刪除操作
刪除是指從陣列中刪除現有元素並重新組織陣列的所有元素。
示例
在這裡,我們使用 python 內建的 remove() 方法刪除陣列中間的資料元素。
from array import *
array1 = array('i', [10,20,30,40,50])
array1.remove(40)
for x in array1:
print(x)
輸出
當我們編譯並執行上述程式時,它會產生以下結果,該結果顯示元素已從陣列中刪除。
10 20 30 50
搜尋操作
您可以根據元素的值或索引執行陣列元素的搜尋。
示例
在這裡,我們使用 python 內建的 index() 方法搜尋資料元素。
from array import *
array1 = array('i', [10,20,30,40,50])
print (array1.index(40))
輸出
當我們編譯並執行上述程式時,它會產生以下結果,該結果顯示元素的索引。如果陣列中不存在該值,則程式會返回錯誤。
3
更新操作
更新操作是指更新給定索引處陣列中的現有元素。
示例
在這裡,我們只需將新值重新分配到我們要更新的所需索引。
from array import *
array1 = array('i', [10,20,30,40,50])
array1[2] = 80
for x in array1:
print(x)
輸出
當我們編譯並執行上述程式時,它會產生以下結果,該結果顯示索引位置 2 的新值。
10 20 80 40 50
Python - 列表
列表是 Python 中最通用的資料型別,可以寫成方括號之間用逗號分隔的值(項)的列表。關於列表的重要一點是,列表中的項不必是相同型別。
建立列表就像在方括號之間放置不同的逗號分隔的值一樣簡單。
例如
list1 = ['physics', 'chemistry', 1997, 2000] list2 = [1, 2, 3, 4, 5 ] list3 = ["a", "b", "c", "d"]
類似於字串索引,列表索引從 0 開始,並且可以對列表進行切片、連線等等。
訪問值
要訪問列表中的值,請使用方括號進行切片,並使用索引或索引來獲取該索引處的值。
例如
#!/usr/bin/python
list1 = ['physics', 'chemistry', 1997, 2000]
list2 = [1, 2, 3, 4, 5, 6, 7 ]
print ("list1[0]: ", list1[0])
print ("list2[1:5]: ", list2[1:5])
當執行上述程式碼時,它會產生以下結果:
list1[0]: physics list2[1:5]: [2, 3, 4, 5]
更新列表
您可以透過在賦值運算子左側進行切片來更新列表的單個或多個元素,並且可以使用 append() 方法向列表中新增元素。
例如
#!/usr/bin/python
list = ['physics', 'chemistry', 1997, 2000]
print ("Value available at index 2 : ")
print (list[2])
list[2] = 2001
print ("New value available at index 2 : ")
print (list[2])
注意 - append() 方法將在後續部分中討論。
當執行上述程式碼時,它會產生以下結果:
Value available at index 2 : 1997 New value available at index 2 : 2001
刪除列表元素
要刪除列表元素,如果確切知道要刪除哪個元素,則可以使用 del 語句;如果不知道,則可以使用 remove() 方法。
例如
#!/usr/bin/python
list1 = ['physics', 'chemistry', 1997, 2000]
print (list1)
del list1[2]
print ("After deleting value at index 2 : ")
print (list1)
當執行上述程式碼時,它會產生以下結果:
['physics', 'chemistry', 1997, 2000] After deleting value at index 2 : ['physics', 'chemistry', 2000]
注意 - remove() 方法將在後續部分中討論。
基本列表操作
列表對 + 和 * 運算子的響應與字串非常相似;它們在這裡也表示連線和重複,只是結果是一個新列表,而不是字串。
事實上,列表對我們在上一章中對字串使用過的所有通用序列操作都有響應。
| Python 表示式 | 結果 | 描述 |
|---|---|---|
| len([1, 2, 3]) | 3 | 長度 |
| [1, 2, 3] + [4, 5, 6] | [1, 2, 3, 4, 5, 6] | 連線 |
| ['Hi!'] * 4 | ['Hi!', 'Hi!', 'Hi!', 'Hi!'] | 重複 |
| 3 in [1, 2, 3] | True | 成員資格 |
| for x in [1, 2, 3]: print x, | 1 2 3 | 迭代 |
Python - 元組
元組是不可變的 Python 物件的序列。元組是序列,就像列表一樣。元組和列表之間的區別在於,元組不能像列表那樣更改,並且元組使用括號,而列表使用方括號。
建立元組就像放置不同的逗號分隔的值一樣簡單。可以選擇將這些逗號分隔的值放在括號之間。
例如
tup1 = ('physics', 'chemistry', 1997, 2000);
tup2 = (1, 2, 3, 4, 5 );
tup3 = "a", "b", "c", "d";
空元組寫成兩個不包含任何內容的括號 - {}。
tup1 = ();
要編寫包含單個值的元組,您必須包含逗號,即使只有一個值 - {}。
tup1 = (50,);
類似於字串索引,元組索引從 0 開始,並且可以對它們進行切片、連線等等。
訪問元組中的值
要訪問元組中的值,請使用方括號進行切片,並使用索引或索引來獲取該索引處的值。
例如
#!/usr/bin/python
tup1 = ('physics', 'chemistry', 1997, 2000);
tup2 = (1, 2, 3, 4, 5, 6, 7 );
print ("tup1[0]: ", tup1[0])
print ("tup2[1:5]: ", tup2[1:5])
當執行上述程式碼時,它會產生以下結果:
tup1[0]: physics tup2[1:5]: [2, 3, 4, 5]
更新元組
元組是不可變的,這意味著您不能更新或更改元組元素的值。您可以使用現有元組的部分來建立新的元組,如下面的示例所示:
#!/usr/bin/python
tup1 = (12, 34.56);
tup2 = ('abc', 'xyz');
# Following action is not valid for tuples
# tup1[0] = 100;
# So let's create a new tuple as follows
tup3 = tup1 + tup2;
print (tup3);
當執行上述程式碼時,它會產生以下結果:
(12, 34.56, 'abc', 'xyz')
刪除元組元素
無法刪除單個元組元素。當然,將另一個元組放在一起並丟棄不需要的元素沒有任何問題。
要顯式刪除整個元組,只需使用del語句即可。
例如
#!/usr/bin/python
tup = ('physics', 'chemistry', 1997, 2000);
print (tup);
del tup;
print ("After deleting tup : ");
print (tup);
注意 - 丟擲異常,這是因為在del tup之後,元組不再存在。
這會產生以下結果:
('physics', 'chemistry', 1997, 2000)
After deleting tup :
Traceback (most recent call last):
File "test.py", line 9, in <module>
print tup;
NameError: name 'tup' is not defined
基本元組操作
元組對 + 和 * 運算子的響應與字串非常相似;它們在這裡也表示連線和重複,只是結果是一個新的元組,而不是字串。
事實上,元組對我們在上一章中對字串使用過的所有通用序列操作都有響應。
| Python 表示式 | 結果 | 描述 |
|---|---|---|
| len((1, 2, 3)) | 3 | 長度 |
| (1, 2, 3) + (4, 5, 6) | (1, 2, 3, 4, 5, 6) | 連線 |
| ('Hi!',) * 4 | ('Hi!', 'Hi!', 'Hi!', 'Hi!') | 重複 |
| 3 in (1, 2, 3) | True | 成員資格 |
| for x in (1, 2, 3): print x, | 1 2 3 | 迭代 |
Python - 字典
在字典中,每個鍵與其值之間用冒號 (:) 分隔,項用逗號分隔,整個內容用花括號括起來。一個沒有任何項的空字典只寫成兩個花括號,如下所示 - {}。
鍵在字典中是唯一的,而值則不一定唯一。字典的值可以是任何型別,但鍵必須是不可變的資料型別,例如字串、數字或元組。
訪問字典中的值
要訪問字典元素,您可以使用熟悉的方括號以及鍵來獲取其值。
示例
一個簡單的示例如下所示:
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
print ("dict['Name']: ", dict['Name'])
print ("dict['Age']: ", dict['Age'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Name']: Zara dict['Age']: 7
如果我們嘗試訪問字典中不存在的鍵對應的值,則會得到如下錯誤:
示例
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
print ("dict['Alice']: ", dict['Alice'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Alice']:
Traceback (most recent call last):
File "test.py", line 4, in <module>
print "dict['Alice']: ", dict['Alice'];
KeyError: 'Alice'
更新字典
您可以透過新增新條目或鍵值對、修改現有條目或刪除現有條目來更新字典,如下面的簡單示例所示:
示例
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
dict['Age'] = 8; # update existing entry
dict['School'] = "DPS School"; # Add new entry
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Age']: 8 dict['School']: DPS School
刪除字典元素
您可以刪除單個字典元素或清除字典的全部內容。您也可以透過單個操作刪除整個字典。
示例
要顯式刪除整個字典,只需使用 **del** 語句。一個簡單的示例如下所示:
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
del dict['Name']; # remove entry with key 'Name'
dict.clear(); # remove all entries in dict
del dict ; # delete entire dictionary
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
**注意** - 因為在 **del dict** 之後,字典就不再存在了,所以會引發異常。
輸出
這會產生以下結果:
dict['Age']: dict['Age'] dict['School']: dict['School']
**注意** - del() 方法將在後續章節中討論。
字典鍵的屬性
字典值沒有任何限制。它們可以是任何任意的 Python 物件,無論是標準物件還是使用者定義的物件。但是,鍵則不是這樣。
關於字典鍵,有兩點需要注意:
每個鍵只能有一個條目。這意味著不允許重複鍵。當在賦值期間遇到重複鍵時,最後一次賦值會生效。
例如
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Name': 'Manni'}
print ("dict['Name']: ", dict['Name'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Name']: Manni
鍵必須是不可變的。這意味著您可以使用字串、數字或元組作為字典鍵,但諸如 ['key'] 之類的東西是不允許的。
示例
一個例子如下:
#!/usr/bin/python
dict = {['Name']: 'Zara', 'Age': 7}
print ("dict['Name']: ", dict['Name'])
輸出
當執行上述程式碼時,它會產生以下結果:
Traceback (most recent call last):
File "test.py", line 3, in <module>
dict = {['Name']: 'Zara', 'Age': 7};
TypeError: list objects are unhashable
Python - 二維陣列
二維陣列是在陣列內的陣列。它是一個數組的陣列。在這種型別的陣列中,資料元素的位置由兩個索引而不是一個索引來引用。因此,它表示一個包含資料行和列的表格。
在下面的二維陣列示例中,觀察到每個陣列元素本身也是一個數組。
考慮每天記錄 4 次溫度的例子。有時記錄儀器可能出現故障,導致我們無法記錄資料。4 天的此類資料可以表示為如下所示的二維陣列。
Day 1 - 11 12 5 2 Day 2 - 15 6 10 Day 3 - 10 8 12 5 Day 4 - 12 15 8 6
上述資料可以用如下所示的二維陣列表示。
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
訪問值
二維陣列中的資料元素可以使用兩個索引訪問。一個索引引用主陣列或父陣列,另一個索引引用資料元素在內部陣列中的位置。如果我們只提及一個索引,則會列印該索引位置的整個內部陣列。
示例
下面的示例說明了它是如何工作的。
from array import * T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]] print(T[0]) print(T[1][2])
輸出
當執行上述程式碼時,它會產生以下結果:
[11, 12, 5, 2] 10
要打印出整個二維陣列,我們可以使用 python for 迴圈,如下所示。我們使用換行符在不同的行中打印出值。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
for r in T:
for c in r:
print(c,end = " ")
print()
輸出
當執行上述程式碼時,它會產生以下結果:
11 12 5 2 15 6 10 10 8 12 5 12 15 8 6
插入值
我們可以使用 insert() 方法並指定索引,在特定位置插入新的資料元素。
示例
在下面的示例中,一個新的資料元素插入到索引位置 2。
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T.insert(2, [0,5,11,13,6])
for r in T:
for c in r:
print(c,end = " ")
print()
輸出
當執行上述程式碼時,它會產生以下結果:
11 12 5 2 15 6 10 0 5 11 13 6 10 8 12 5 12 15 8 6
更新值
我們可以透過使用陣列索引重新賦值來更新整個內部陣列或內部陣列的一些特定資料元素。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T[2] = [11,9]
T[0][3] = 7
for r in T:
for c in r:
print(c,end = " ")
print()
輸出
當執行上述程式碼時,它會產生以下結果:
11 12 5 7 15 6 10 11 9 12 15 8 6
刪除值
我們可以透過使用帶索引的 del() 方法重新賦值來刪除整個內部陣列或內部陣列的一些特定資料元素。但是,如果您需要刪除其中一個內部陣列中的特定資料元素,則使用上面描述的更新過程。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
del T[3]
for r in T:
for c in r:
print(c,end = " ")
print()
輸出
當執行上述程式碼時,它會產生以下結果:
11 12 5 2 15 6 10 10 8 12 5
Python - 矩陣
矩陣是二維陣列的一種特殊情況,其中每個資料元素的大小都嚴格相同。因此,每個矩陣也是一個二維陣列,反之則不然。
矩陣對於許多數學和科學計算來說是非常重要的資料結構。由於我們已經在上一章中討論了二維陣列資料結構,因此本章將重點介紹特定於矩陣的資料結構操作。
我們還將使用 numpy 包進行矩陣資料操作。
矩陣示例
考慮記錄一週溫度的案例,在早上、中午、晚上和午夜測量。它可以使用陣列和 numpy 中可用的 reshape 方法表示為 7X5 矩陣。
from numpy import * a = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = reshape(a,(7,5)) print(m)
輸出
上述資料可以用如下所示的二維陣列表示:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
訪問值
矩陣中的資料元素可以透過使用索引來訪問。訪問方法與在二維陣列中訪問資料的方式相同。
示例
from numpy import *
m = array([['Mon',18,20,22,17],['Tue',11,18,21,18],
['Wed',15,21,20,19],['Thu',11,20,22,21],
['Fri',18,17,23,22],['Sat',12,22,20,18],
['Sun',13,15,19,16]])
# Print data for Wednesday
print(m[2])
# Print data for friday evening
print(m[4][3])
輸出
當執行上述程式碼時,它會產生以下結果:
['Wed', 15, 21, 20, 19] 23
新增一行
使用下面提到的程式碼在矩陣中新增一行。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m_r = append(m,[['Avg',12,15,13,11]],0) print(m_r)
輸出
當執行上述程式碼時,它會產生以下結果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ['Avg' '12' '15' '13' '11'] ]
新增一列
我們可以使用 insert() 方法向矩陣新增列。在這裡,我們必須提及要新增列的索引以及包含新增列的新值的陣列。在下面的示例中,我們在從開頭算起的第五個位置添加了一列。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m_c = insert(m,[5],[[1],[2],[3],[4],[5],[6],[7]],1) print(m_c)
輸出
當執行上述程式碼時,它會產生以下結果:
[ ['Mon' '18' '20' '22' '17' '1'] ['Tue' '11' '18' '21' '18' '2'] ['Wed' '15' '21' '20' '19' '3'] ['Thu' '11' '20' '22' '21' '4'] ['Fri' '18' '17' '23' '22' '5'] ['Sat' '12' '22' '20' '18' '6'] ['Sun' '13' '15' '19' '16' '7'] ]
刪除一行
我們可以使用 delete() 方法從矩陣中刪除一行。我們必須指定行的索引以及軸值,對於行,軸值為 0,對於列,軸值為 1。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = delete(m,[2],0) print(m)
輸出
當執行上述程式碼時,它會產生以下結果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
刪除一列
我們可以使用 delete() 方法從矩陣中刪除一列。我們必須指定列的索引以及軸值,對於行,軸值為 0,對於列,軸值為 1。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = delete(m,s_[2],1) print(m)
輸出
當執行上述程式碼時,它會產生以下結果:
[ ['Mon' '18' '22' '17'] ['Tue' '11' '21' '18'] ['Wed' '15' '20' '19'] ['Thu' '11' '22' '21'] ['Fri' '18' '23' '22'] ['Sat' '12' '20' '18'] ['Sun' '13' '19' '16'] ]
更新一行
要更新矩陣中行的值,我們只需重新分配行索引處的值。在下面的示例中,星期四的所有資料都標記為零。此行的索引為 3。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m[3] = ['Thu',0,0,0,0] print(m)
輸出
當執行上述程式碼時,它會產生以下結果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '0' '0' '0' '0'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
Python - 集合
在數學上,集合是一組專案,沒有特定的順序。Python 集合類似於此數學定義,並具有以下附加條件。
集合中的元素不能重複。
集合中的元素是不可變的(不能修改),但集合作為一個整體是可變的。
Python 集合中的任何元素都沒有附加索引。因此,它們不支援任何索引或切片操作。
集合操作
Python 中的集合通常用於數學運算,如並集、交集、差集和補集等。我們可以建立一個集合,訪問其元素並執行這些數學運算,如下所示。
建立集合
集合是透過使用 set() 函式或將所有元素放在一對花括號內來建立的。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
Months={"Jan","Feb","Mar"}
Dates={21,22,17}
print(Days)
print(Months)
print(Dates)
輸出
執行上述程式碼時,會產生以下結果。請注意結果中元素的順序是如何改變的。
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat']) set(['Jan', 'Mar', 'Feb']) set([17, 21, 22])
我們無法訪問集合中的單個值。我們只能像上面那樣一起訪問所有元素。但是我們也可以透過迴圈遍歷集合來獲取單個元素的列表。
訪問集合中的值
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"]) for d in Days: print(d)
輸出
當執行上述程式碼時,它會產生以下結果:
Wed Sun Fri Tue Mon Thu Sat
向集合中新增專案
我們可以使用 add() 方法向集合中新增元素。同樣,正如我們所討論的,新新增的元素沒有附加特定的索引。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat"])
Days.add("Sun")
print(Days)
輸出
當執行上述程式碼時,它會產生以下結果:
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
從集合中刪除專案
我們可以使用 discard() 方法從集合中刪除元素。同樣,正如我們所討論的,新新增的元素沒有附加特定的索引。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat"])
Days.discard("Sun")
print(Days)
輸出
執行上述程式碼時,會產生以下結果。
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
集合的並集
兩個集合的並集操作會生成一個新的集合,其中包含兩個集合中所有不同的元素。在下面的示例中,元素“Wed”同時存在於兩個集合中。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA|DaysB print(AllDays)
輸出
執行上述程式碼時,會產生以下結果。請注意,結果中只有一個“wed”。
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
集合的交集
兩個集合的交集操作會生成一個新的集合,其中僅包含兩個集合中共同的元素。在下面的示例中,元素“Wed”同時存在於兩個集合中。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA & DaysB print(AllDays)
輸出
執行上述程式碼時,會產生以下結果。請注意,結果中只有一個“wed”。
set(['Wed'])
集合的差集
兩個集合的差集操作會生成一個新的集合,其中僅包含第一個集合中的元素,而不包含第二個集合中的元素。在下面的示例中,元素“Wed”同時存在於兩個集合中,因此在結果集中將找不到它。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA - DaysB print(AllDays)
輸出
執行上述程式碼時,會產生以下結果。請注意,結果中只有一個“wed”。
set(['Mon', 'Tue'])
比較集合
我們可以檢查給定的集合是否是另一個集合的子集或超集。結果為 True 或 False,具體取決於集合中存在的元素。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"]) SubsetRes = DaysA <= DaysB SupersetRes = DaysB >= DaysA print(SubsetRes) print(SupersetRes)
輸出
當執行上述程式碼時,它會產生以下結果:
True True
Python - 對映
Python 對映,也稱為 ChainMap,是一種資料結構,用於將多個字典作為一個單元一起管理。組合字典包含以特定順序排列的鍵值對,消除了任何重複的鍵。ChainMap 的最佳用途是同時搜尋多個字典並獲得正確的鍵值對對映。我們還看到這些 ChainMap 具有棧資料結構的行為。
建立 ChainMap
我們建立兩個字典,並使用 collections 庫中的 ChainMap 方法將它們組合在一起。然後,我們列印組合字典結果的鍵和值。如果存在重複鍵,則僅保留第一個鍵的值。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day1': 'Thu'}
res = collections.ChainMap(dict1, dict2)
# Creating a single dictionary
print(res.maps,'\n')
print('Keys = {}'.format(list(res.keys())))
print('Values = {}'.format(list(res.values())))
print()
# Print all the elements from the result
print('elements:')
for key, val in res.items():
print('{} = {}'.format(key, val))
print()
# Find a specific value in the result
print('day3 in res: {}'.format(('day1' in res)))
print('day4 in res: {}'.format(('day4' in res)))
輸出
當執行上述程式碼時,它會產生以下結果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day1': 'Thu', 'day3': 'Wed'}]
Keys = ['day1', 'day3', 'day2']
Values = ['Mon', 'Wed', 'Tue']
elements:
day1 = Mon
day3 = Wed
day2 = Tue
day3 in res: True
day4 in res: False
對映重新排序
如果我們在上面的示例中更改字典的組合順序,我們會看到元素的位置會互換,就像它們在一個連續的鏈中一樣。這再次表明對映作為棧的行為。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day4': 'Thu'}
res1 = collections.ChainMap(dict1, dict2)
print(res1.maps,'\n')
res2 = collections.ChainMap(dict2, dict1)
print(res2.maps,'\n')
輸出
當執行上述程式碼時,它會產生以下結果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Thu'}]
[{'day3': 'Wed', 'day4': 'Thu'}, {'day1': 'Mon', 'day2': 'Tue'}]
更新對映
當字典的元素更新時,結果會立即更新到 ChainMap 的結果中。在下面的示例中,我們看到新的更新值反映在結果中,而無需再次顯式應用 ChainMap 方法。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day4': 'Thu'}
res = collections.ChainMap(dict1, dict2)
print(res.maps,'\n')
dict2['day4'] = 'Fri'
print(res.maps,'\n')
輸出
當執行上述程式碼時,它會產生以下結果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Thu'}]
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Fri'}]
Python - 連結串列
連結串列是一系列資料元素,它們透過連結連線在一起。每個資料元素都包含一個指向另一個數據元素的指標。Python 的標準庫中沒有連結串列。我們使用節點的概念來實現連結串列的概念,如上一章所述。
我們已經瞭解瞭如何建立節點類以及如何遍歷節點的元素。在本章中,我們將研究稱為單鏈表的連結串列型別。在這種資料結構中,任意兩個資料元素之間只有一個連結。我們建立這樣的列表,並建立其他方法來插入、更新和刪除列表中的元素。
連結串列的建立
連結串列是使用上一章中學習的節點類建立的。我們建立一個 Node 物件,並建立另一個類來使用此 ode 物件。我們透過節點物件傳遞適當的值以指向下一個資料元素。下面的程式建立了包含三個資料元素的連結串列。在下一節中,我們將瞭解如何遍歷連結串列。
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
list1 = SLinkedList()
list1.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list1.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
遍歷連結串列
單鏈表只能從第一個資料元素開始向前遍歷。我們只需透過將下一個節點的指標分配給當前資料元素來列印下一個資料元素的值。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
list.listprint()
輸出
當執行上述程式碼時,它會產生以下結果:
Mon Tue Wed
在連結串列中插入
在連結串列中插入元素涉及重新分配現有節點到新插入節點的指標。根據新資料元素是在連結串列的開頭、中間還是末尾插入,我們有以下幾種情況。
在開頭插入
這涉及將新資料節點的下一個指標指向連結串列的當前頭部。因此,連結串列的當前頭部成為第二個資料元素,而新節點成為連結串列的頭部。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
def AtBegining(self,newdata):
NewNode = Node(newdata)
# Update the new nodes next val to existing node
NewNode.nextval = self.headval
self.headval = NewNode
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtBegining("Sun")
list.listprint()
輸出
當執行上述程式碼時,它會產生以下結果:
Sun Mon Tue Wed
在末尾插入
這涉及將連結串列的當前最後一個節點的下一個指標指向新資料節點。因此,連結串列的當前最後一個節點成為倒數第二個資料節點,而新節點成為連結串列的最後一個節點。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add newnode
def AtEnd(self, newdata):
NewNode = Node(newdata)
if self.headval is None:
self.headval = NewNode
return
laste = self.headval
while(laste.nextval):
laste = laste.nextval
laste.nextval=NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtEnd("Thu")
list.listprint()
輸出
當執行上述程式碼時,它會產生以下結果:
Mon Tue Wed Thu
在兩個資料節點之間插入
這涉及更改特定節點的指標以指向新節點。這可以透過同時傳遞新節點和新節點將要插入其後的現有節點來實現。因此,我們定義了一個額外的類,它將更改新節點的下一個指標以指向中間節點的下一個指標。然後將新節點分配給中間節點的下一個指標。
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add node
def Inbetween(self,middle_node,newdata):
if middle_node is None:
print("The mentioned node is absent")
return
NewNode = Node(newdata)
NewNode.nextval = middle_node.nextval
middle_node.nextval = NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Thu")
list.headval.nextval = e2
e2.nextval = e3
list.Inbetween(list.headval.nextval,"Fri")
list.listprint()
輸出
當執行上述程式碼時,它會產生以下結果:
Mon Tue Fri Thu
刪除專案
我們可以使用節點的鍵來刪除現有節點。在下面的程式中,我們找到要刪除的節點的前一個節點。然後,將此節點的 next 指標指向要刪除的節點的下一個節點。
示例
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLinkedList:
def __init__(self):
self.head = None
def Atbegining(self, data_in):
NewNode = Node(data_in)
NewNode.next = self.head
self.head = NewNode
# Function to remove node
def RemoveNode(self, Removekey):
HeadVal = self.head
if (HeadVal is not None):
if (HeadVal.data == Removekey):
self.head = HeadVal.next
HeadVal = None
return
while (HeadVal is not None):
if HeadVal.data == Removekey:
break
prev = HeadVal
HeadVal = HeadVal.next
if (HeadVal == None):
return
prev.next = HeadVal.next
HeadVal = None
def LListprint(self):
printval = self.head
while (printval):
print(printval.data),
printval = printval.next
llist = SLinkedList()
llist.Atbegining("Mon")
llist.Atbegining("Tue")
llist.Atbegining("Wed")
llist.Atbegining("Thu")
llist.RemoveNode("Tue")
llist.LListprint()
輸出
當執行上述程式碼時,它會產生以下結果:
Thu Wed Mon
Python - 棧
在英語詞典中,stack(棧)一詞表示將物體一個疊一個地堆放。這與這種資料結構中記憶體的分配方式相同。它以類似於廚房裡一堆盤子一個疊一個地存放的方式儲存資料元素。因此,棧資料結構允許在一端進行操作,這可以稱為棧的頂部。我們只能從此棧端新增或刪除元素。
在棧中,最後插入的元素將首先出來,因為我們只能從棧頂刪除。這種特性稱為後進先出 (LIFO) 特性。新增和刪除元素的操作稱為 **PUSH** 和 **POP**。在下面的程式中,我們將其實現為 **add** 和 **remove** 函式。我們宣告一個空列表,並使用 append() 和 pop() 方法來新增和刪除資料元素。
將元素壓入棧
讓我們瞭解如何在棧中使用 PUSH。請參考下面提到的程式 -
示例
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use peek to look at the top of the stack
def peek(self):
return self.stack[-1]
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.peek()
print(AStack.peek())
AStack.add("Wed")
AStack.add("Thu")
print(AStack.peek())
輸出
當執行上述程式碼時,它會產生以下結果:
Tue Thu
從棧中彈出元素
正如我們所知,我們只能從棧中刪除最頂部的元素,我們實現了一個 Python 程式來執行此操作。以下程式中的 remove 函式返回最頂部的元素。我們首先計算棧的大小來檢查頂部元素,然後使用內建的 pop() 方法找出最頂部的元素。
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use list pop method to remove element
def remove(self):
if len(self.stack) <= 0:
return ("No element in the Stack")
else:
return self.stack.pop()
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.add("Wed")
AStack.add("Thu")
print(AStack.remove())
print(AStack.remove())
輸出
當執行上述程式碼時,它會產生以下結果:
Thu Wed
Python - 佇列
我們在日常生活中都熟悉佇列,因為我們等待服務。佇列資料結構也意味著相同,其中資料元素按佇列排列。佇列的獨特性在於新增和刪除專案的方式。專案在一端允許,但在另一端刪除。因此,它是一種先進先出方法。
可以使用 Python 列表實現佇列,其中我們可以使用 insert() 和 pop() 方法新增和刪除元素。沒有插入,因為資料元素始終新增到佇列的末尾。
新增元素
在下面的示例中,我們建立一個佇列類,其中我們實現了先進先出方法。我們使用內建的 insert 方法新增資料元素。
示例
class Queue:
def __init__(self):
self.queue = list()
def addtoq(self,dataval):
# Insert method to add element
if dataval not in self.queue:
self.queue.insert(0,dataval)
return True
return False
def size(self):
return len(self.queue)
TheQueue = Queue()
TheQueue.addtoq("Mon")
TheQueue.addtoq("Tue")
TheQueue.addtoq("Wed")
print(TheQueue.size())
輸出
當執行上述程式碼時,它會產生以下結果:
3
刪除元素
在下面的示例中,我們建立一個佇列類,其中我們插入資料,然後使用內建的 pop 方法刪除資料。
示例
class Queue:
def __init__(self):
self.queue = list()
def addtoq(self,dataval):
# Insert method to add element
if dataval not in self.queue:
self.queue.insert(0,dataval)
return True
return False
# Pop method to remove element
def removefromq(self):
if len(self.queue)>0:
return self.queue.pop()
return ("No elements in Queue!")
TheQueue = Queue()
TheQueue.addtoq("Mon")
TheQueue.addtoq("Tue")
TheQueue.addtoq("Wed")
print(TheQueue.removefromq())
print(TheQueue.removefromq())
輸出
當執行上述程式碼時,它會產生以下結果:
Mon Tue
Python - 雙端佇列
雙端佇列(或 deque)支援從任一端新增和刪除元素。更常用的棧和佇列是雙端佇列的簡併形式,其中輸入和輸出限制在一端。
示例
import collections
DoubleEnded = collections.deque(["Mon","Tue","Wed"])
DoubleEnded.append("Thu")
print ("Appended at right - ")
print (DoubleEnded)
DoubleEnded.appendleft("Sun")
print ("Appended at right at left is - ")
print (DoubleEnded)
DoubleEnded.pop()
print ("Deleting from right - ")
print (DoubleEnded)
DoubleEnded.popleft()
print ("Deleting from left - ")
print (DoubleEnded)
輸出
當執行上述程式碼時,它會產生以下結果:
Appended at right - deque(['Mon', 'Tue', 'Wed', 'Thu']) Appended at right at left is - deque(['Sun', 'Mon', 'Tue', 'Wed', 'Thu']) Deleting from right - deque(['Sun', 'Mon', 'Tue', 'Wed']) Deleting from left - deque(['Mon', 'Tue', 'Wed'])
Python - 高階連結串列
我們已經在前面章節中看到了連結串列,其中只能向前遍歷。在本節中,我們看到另一種型別的連結串列,其中可以向前和向後遍歷。這種連結串列稱為雙向連結串列。以下是雙向連結串列的特點。
雙向連結串列包含一個稱為 first 和 last 的連結元素。
每個連結都包含一個數據欄位和兩個連結欄位,稱為 next 和 prev。
每個連結都使用其 next 連結與其下一個連結連結。
每個連結都使用其 previous 連結與其上一個連結連結。
最後一個連結帶有 null 連結以標記列表的末尾。
建立雙向連結串列
我們使用 Node 類建立雙向連結串列。現在我們使用與單向連結串列中相同的方法,但 head 和 next 指標將用於正確分配,以在每個節點中建立兩個連結,此外還有節點中存在的資料。
示例
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
class doubly_linked_list:
def __init__(self):
self.head = None
# Adding data elements
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Print the Doubly Linked list
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.push(8)
dllist.push(62)
dllist.listprint(dllist.head)
輸出
當執行上述程式碼時,它會產生以下結果:
62 8 12
插入雙向連結串列
在這裡,我們將瞭解如何使用以下程式將節點插入雙向連結串列。該程式使用名為 insert 的方法,該方法將新節點插入雙向連結串列頭部的第三個位置。
示例
# Create the Node class
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
# Create the doubly linked list
class doubly_linked_list:
def __init__(self):
self.head = None
# Define the push method to add elements
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Define the insert method to insert the element
def insert(self, prev_node, NewVal):
if prev_node is None:
return
NewNode = Node(NewVal)
NewNode.next = prev_node.next
prev_node.next = NewNode
NewNode.prev = prev_node
if NewNode.next is not None:
NewNode.next.prev = NewNode
# Define the method to print the linked list
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.push(8)
dllist.push(62)
dllist.insert(dllist.head.next, 13)
dllist.listprint(dllist.head)
輸出
當執行上述程式碼時,它會產生以下結果:
62 8 13 12
追加到雙向連結串列
追加到雙向連結串列將把元素新增到末尾。
示例
# Create the node class
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
# Create the doubly linked list class
class doubly_linked_list:
def __init__(self):
self.head = None
# Define the push method to add elements at the begining
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Define the append method to add elements at the end
def append(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = None
if self.head is None:
NewNode.prev = None
self.head = NewNode
return
last = self.head
while (last.next is not None):
last = last.next
last.next = NewNode
NewNode.prev = last
return
# Define the method to print
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.append(9)
dllist.push(8)
dllist.push(62)
dllist.append(45)
dllist.listprint(dllist.head)
輸出
當執行上述程式碼時,它會產生以下結果:
62 8 12 9 45
請注意追加操作中元素 9 和 45 的位置。
Python - 雜湊表
雜湊表是一種資料結構,其中資料元素的地址或索引值是由雜湊函式生成的。這使得訪問資料更快,因為索引值充當資料值的鍵。換句話說,雜湊表儲存鍵值對,但鍵是透過雜湊函式生成的。
因此,資料元素的搜尋和插入函式變得更快,因為鍵值本身成為儲存資料的陣列的索引。
在 Python 中,字典資料型別表示雜湊表的實現。字典中的鍵滿足以下要求。
字典的鍵是可雜湊的,即它們是由雜湊函式生成的,該雜湊函式為提供給它的每個唯一值生成唯一的結果。
字典中資料元素的順序不固定。
因此,我們看到如下使用字典資料型別實現雜湊表。
訪問字典中的值
要訪問字典元素,您可以使用熟悉的方括號以及鍵來獲取其值。
示例
# Declare a dictionary
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
# Accessing the dictionary with its key
print ("dict['Name']: ", dict['Name'])
print ("dict['Age']: ", dict['Age'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Name']: Zara dict['Age']: 7
更新字典
您可以透過新增新條目或鍵值對、修改現有條目或刪除現有條目來更新字典,如下面的簡單示例所示:
示例
# Declare a dictionary
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
dict['Age'] = 8; # update existing entry
dict['School'] = "DPS School"; # Add new entry
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
輸出
當執行上述程式碼時,它會產生以下結果:
dict['Age']: 8 dict['School']: DPS School
刪除字典元素
您可以刪除單個字典元素或清除字典的全部內容。您也可以在單個操作中刪除整個字典。要顯式刪除整個字典,只需使用 del 語句。
示例
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
del dict['Name']; # remove entry with key 'Name'
dict.clear(); # remove all entries in dict
del dict ; # delete entire dictionary
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
輸出
這將產生以下結果。請注意,由於 del dict 後字典不再存在,因此會引發異常。
dict['Age']: dict['Age'] dict['School']: dict['School']
Python - 二叉樹
樹表示由邊連線的節點。它是一種非線性資料結構。它具有以下屬性 -
一個節點被標記為根節點。
除根節點外的每個節點都與一個父節點相關聯。
每個節點可以有任意數量的子節點。
我們透過使用前面討論的節點概念在 Python 中建立樹資料結構。我們指定一個節點作為根節點,然後新增更多節點作為子節點。以下是建立根節點的程式。
建立根節點
我們只建立一個 Node 類併為節點分配一個值。這成為只有一棵根節點的樹。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def PrintTree(self):
print(self.data)
root = Node(10)
root.PrintTree()
輸出
當執行上述程式碼時,它會產生以下結果:
10
插入樹
要插入樹,我們使用上面建立的相同 Node 類,並向其中新增 insert 類。insert 類將節點的值與父節點的值進行比較,並決定將其新增為左節點還是右節點。最後,PrintTree 類用於列印樹。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
# Compare the new value with the parent node
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Use the insert method to add nodes
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)
root.PrintTree()
輸出
當執行上述程式碼時,它會產生以下結果:
3 6 12 14
遍歷樹
可以透過決定訪問每個節點的順序來遍歷樹。正如我們清楚地看到的那樣,我們可以從一個節點開始,然後先訪問左子樹,然後訪問右子樹。或者我們也可以先訪問右子樹,然後訪問左子樹。因此,這些樹遍歷方法有不同的名稱。
樹遍歷演算法
遍歷是訪問樹的所有節點的過程,也可能列印它們的值。因為所有節點都透過邊(連結)連線,所以我們總是從根(頭部)節點開始。也就是說,我們無法隨機訪問樹中的節點。我們使用三種方法來遍歷樹。
中序遍歷
先序遍歷
後序遍歷
中序遍歷
在這種遍歷方法中,先訪問左子樹,然後訪問根節點,最後訪問右子樹。我們應該始終記住,每個節點都可以表示一個子樹本身。
在下面的 Python 程式中,我們使用 Node 類為根節點以及左節點和右節點建立佔位符。然後,我們建立一個 insert 函式將資料新增到樹中。最後,透過建立一個空列表並將左節點首先新增到列表中,然後是根節點或父節點,實現了中序遍歷邏輯。
最後,新增左節點以完成中序遍歷。請注意,此過程會針對每個子樹重複,直到遍歷所有節點。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Inorder traversal
# Left -> Root -> Right
def inorderTraversal(self, root):
res = []
if root:
res = self.inorderTraversal(root.left)
res.append(root.data)
res = res + self.inorderTraversal(root.right)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.inorderTraversal(root))
輸出
當執行上述程式碼時,它會產生以下結果:
[10, 14, 19, 27, 31, 35, 42]
先序遍歷
在這種遍歷方法中,先訪問根節點,然後訪問左子樹,最後訪問右子樹。
在下面的 Python 程式中,我們使用 Node 類為根節點以及左節點和右節點建立佔位符。然後,我們建立一個 insert 函式將資料新增到樹中。最後,透過建立一個空列表並將根節點首先新增到列表中,然後是左節點,實現了先序遍歷邏輯。
最後,新增右節點以完成先序遍歷。請注意,此過程會針對每個子樹重複,直到遍歷所有節點。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Preorder traversal
# Root -> Left ->Right
def PreorderTraversal(self, root):
res = []
if root:
res.append(root.data)
res = res + self.PreorderTraversal(root.left)
res = res + self.PreorderTraversal(root.right)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.PreorderTraversal(root))
輸出
當執行上述程式碼時,它會產生以下結果:
[27, 14, 10, 19, 35, 31, 42]
後序遍歷
在這種遍歷方法中,最後訪問根節點,因此得名。首先,我們遍歷左子樹,然後遍歷右子樹,最後遍歷根節點。
在下面的 Python 程式中,我們使用 Node 類為根節點以及左節點和右節點建立佔位符。然後,我們建立一個 insert 函式將資料新增到樹中。最後,透過建立一個空列表並將左節點首先新增到列表中,然後是右節點,實現了後序遍歷邏輯。
最後,新增根節點或父節點以完成後序遍歷。請注意,此過程會針對每個子樹重複,直到遍歷所有節點。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else if data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Postorder traversal
# Left ->Right -> Root
def PostorderTraversal(self, root):
res = []
if root:
res = self.PostorderTraversal(root.left)
res = res + self.PostorderTraversal(root.right)
res.append(root.data)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.PostorderTraversal(root))
輸出
當執行上述程式碼時,它會產生以下結果:
[10, 19, 14, 31, 42, 35, 27]
Python - 搜尋樹
二叉搜尋樹 (BST) 是一種樹,其中所有節點都遵循以下提到的屬性。節點的左子樹的鍵小於或等於其父節點的鍵。節點的右子樹的鍵大於其父節點的鍵。因此,BST 將其所有子樹劃分為兩個部分;左子樹和右子樹。
left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)
在 B 樹中搜索值
在樹中搜索值涉及將傳入值與退出節點的值進行比較。這裡我們也從左到右遍歷節點,最後再與父節點比較。如果要搜尋的值與任何現有值都不匹配,則返回“未找到”訊息,否則返回“已找到”訊息。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# findval method to compare the value with nodes
def findval(self, lkpval):
if lkpval < self.data:
if self.left is None:
return str(lkpval)+" Not Found"
return self.left.findval(lkpval)
else if lkpval > self.data:
if self.right is None:
return str(lkpval)+" Not Found"
return self.right.findval(lkpval)
else:
print(str(self.data) + ' is found')
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)
print(root.findval(7))
print(root.findval(14))
輸出
當執行上述程式碼時,它會產生以下結果:
7 Not Found 14 is found
Python - 堆
堆是一種特殊的樹結構,其中每個父節點都小於或等於其子節點。然後它被稱為最小堆。如果每個父節點都大於或等於其子節點,則它被稱為最大堆。它在實現優先順序佇列中非常有用,其中權重較高的佇列項在處理中具有更高的優先順序。
我們網站上提供了有關堆的詳細討論。如果您不熟悉堆資料結構,請先學習它。在本節中,我們將看到使用 Python 實現堆資料結構。
建立堆
堆是使用 Python 的內建庫 heapq 建立的。該庫具有執行堆資料結構上各種操作的相關函式。以下是這些函式的列表。
**heapify** - 此函式將常規列表轉換為堆。在生成的堆中,最小的元素被推送到索引位置 0。但其餘資料元素不一定排序。
**heappush** - 此函式將元素新增到堆中,而不會更改當前堆。
**heappop** - 此函式從堆中返回最小的資料元素。
**heapreplace** - 此函式用函式中提供的新值替換最小的資料元素。
建立堆
堆的建立只需使用一個包含元素的列表和堆化函式即可。在下面的示例中,我們提供了一個元素列表,堆化函式會重新排列元素,並將最小的元素放到第一個位置。
示例
import heapq H = [21,1,45,78,3,5] # Use heapify to rearrange the elements heapq.heapify(H) print(H)
輸出
當執行上述程式碼時,它會產生以下結果:
[1, 3, 5, 78, 21, 45]
插入堆
將資料元素插入堆中總是將元素新增到最後一個索引處。但是,您可以再次應用堆化函式,僅當新新增的元素值最小時,才能將其放到第一個索引位置。在下面的示例中,我們插入數字 8。
示例
import heapq H = [21,1,45,78,3,5] # Covert to a heap heapq.heapify(H) print(H) # Add element heapq.heappush(H,8) print(H)
輸出
當執行上述程式碼時,它會產生以下結果:
[1, 3, 5, 78, 21, 45] [1, 3, 5, 78, 21, 45, 8]
從堆中刪除
您可以使用此函式刪除第一個索引處的元素。在下面的示例中,該函式將始終刪除索引位置 1 處的元素。
示例
import heapq H = [21,1,45,78,3,5] # Create the heap heapq.heapify(H) print(H) # Remove element from the heap heapq.heappop(H) print(H)
輸出
當執行上述程式碼時,它會產生以下結果:
[1, 3, 5, 78, 21, 45] [3, 21, 5, 78, 45]
在堆中替換
堆替換函式始終刪除堆中最小的元素,並將新傳入的元素插入到某個位置,該位置不受任何順序的限制。
示例
import heapq H = [21,1,45,78,3,5] # Create the heap heapq.heapify(H) print(H) # Replace an element heapq.heapreplace(H,6) print(H)
輸出
當執行上述程式碼時,它會產生以下結果:
[1, 3, 5, 78, 21, 45] [3, 6, 5, 78, 21, 45]
Python - 圖
圖是物件集合的圖形表示,其中某些物件對透過連結連線。相互連線的物件由稱為頂點的點表示,連線頂點的連結稱為邊。與圖相關的各種術語和功能在我們的教程中進行了詳細描述。
在本章中,我們將學習如何使用 Python 程式建立圖並在其中新增各種資料元素。以下是我們在圖上執行的基本操作。
- 顯示圖的頂點
- 顯示圖的邊
- 新增頂點
- 新增邊
- 建立圖
可以使用 Python 字典資料型別輕鬆地表示圖。我們將頂點表示為字典的鍵,將頂點之間的連線(也稱為邊)表示為字典中的值。
請看以下圖形:

在上圖中,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
示例
我們可以在 Python 程式中如下表示此圖:
# Create the dictionary with graph elements
graph = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
# Print the graph
print(graph)
輸出
當執行上述程式碼時,它會產生以下結果:
{'c': ['a', 'd'], 'a': ['b', 'c'], 'e': ['d'], 'd': ['e'], 'b': ['a', 'd']}
顯示圖的頂點
要顯示圖的頂點,我們只需查詢圖字典的鍵。我們使用 keys() 方法。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = []
self.gdict = gdict
# Get the keys of the dictionary
def getVertices(self):
return list(self.gdict.keys())
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
print(g.getVertices())
輸出
當執行上述程式碼時,它會產生以下結果:
['d', 'b', 'e', 'c', 'a']
顯示圖的邊
查詢圖的邊比頂點稍微複雜一些,因為我們必須找到每對頂點之間是否存在邊。因此,我們建立一個空的邊列表,然後遍歷與每個頂點關聯的邊值。形成一個列表,其中包含從頂點找到的不同邊組。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def edges(self):
return self.findedges()
# Find the distinct list of edges
def findedges(self):
edgename = []
for vrtx in self.gdict:
for nxtvrtx in self.gdict[vrtx]:
if {nxtvrtx, vrtx} not in edgename:
edgename.append({vrtx, nxtvrtx})
return edgename
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
print(g.edges())
輸出
當執行上述程式碼時,它會產生以下結果:
[{'b', 'a'}, {'b', 'd'}, {'e', 'd'}, {'a', 'c'}, {'c', 'd'}]
新增頂點
新增頂點很簡單,我們只需向圖字典新增另一個鍵即可。
示例
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def getVertices(self):
return list(self.gdict.keys())
# Add the vertex as a key
def addVertex(self, vrtx):
if vrtx not in self.gdict:
self.gdict[vrtx] = []
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
g.addVertex("f")
print(g.getVertices())
輸出
當執行上述程式碼時,它會產生以下結果:
['a', 'b', 'c', 'd', 'e','f']
新增邊
向現有圖中新增邊涉及將新頂點視為元組,並驗證邊是否已存在。如果不存在,則新增邊。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def edges(self):
return self.findedges()
# Add the new edge
def AddEdge(self, edge):
edge = set(edge)
(vrtx1, vrtx2) = tuple(edge)
if vrtx1 in self.gdict:
self.gdict[vrtx1].append(vrtx2)
else:
self.gdict[vrtx1] = [vrtx2]
# List the edge names
def findedges(self):
edgename = []
for vrtx in self.gdict:
for nxtvrtx in self.gdict[vrtx]:
if {nxtvrtx, vrtx} not in edgename:
edgename.append({vrtx, nxtvrtx})
return edgename
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
g.AddEdge({'a','e'})
g.AddEdge({'a','c'})
print(g.edges())
輸出
當執行上述程式碼時,它會產生以下結果:
[{'e', 'd'}, {'b', 'a'}, {'b', 'd'}, {'a', 'c'}, {'a', 'e'}, {'c', 'd'}]
Python - 演算法設計
演算法是一個逐步的過程,它定義了一組指令,這些指令按特定順序執行以獲得所需的輸出。演算法通常獨立於底層語言建立,即,演算法可以在多種程式語言中實現。
從資料結構的角度來看,以下是一些重要的演算法類別:
搜尋 - 在資料結構中搜索專案的演算法。
排序 - 按特定順序對專案進行排序的演算法。
插入 - 將專案插入資料結構的演算法。
更新 - 更新資料結構中現有專案的演算法。
刪除 - 從資料結構中刪除現有專案的演算法。
演算法的特徵
並非所有過程都可以稱為演算法。演算法應具有以下特徵:
明確性 - 演算法應清晰明確。它的每個步驟(或階段)及其輸入/輸出都應清晰,並且必須只產生一個含義。
輸入 - 演算法應具有 0 個或多個明確定義的輸入。
輸出 - 演算法應具有 1 個或多個明確定義的輸出,並且應與所需的輸出匹配。
有限性 - 演算法必須在有限的步驟後終止。
可行性 - 應在可用資源下可行。
獨立性 - 演算法應具有分步說明,這些說明應獨立於任何程式設計程式碼。
如何編寫演算法?
沒有編寫演算法的明確標準。相反,它取決於問題和資源。演算法永遠不會編寫為支援特定的程式設計程式碼。
眾所周知,所有程式語言都共享基本的程式碼結構,如迴圈(do、for、while)、流程控制(if-else)等。這些通用結構可用於編寫演算法。
我們以分步方式編寫演算法,但這並非總是如此。演算法編寫是一個過程,在問題域明確定義後執行。也就是說,我們應該知道我們正在為其設計解決方案的問題域。
示例
讓我們嘗試透過一個示例學習演算法編寫。
問題 - 設計一個演算法來新增兩個數字並顯示結果。
步驟 1 - 開始
步驟 2 - 宣告三個整數 a、b 和 c
步驟 3 - 定義 a 和 b 的值
步驟 4 - 新增 a 和 b 的值
步驟 5 - 將步驟 4的輸出儲存到 c 中
步驟 6 - 列印 c
步驟 7 - 停止
演算法告訴程式設計師如何編寫程式。或者,演算法可以寫成:
步驟 1 - 開始新增
步驟 2 - 獲取 a 和 b 的值
步驟 3 - c ← a + b
步驟 4 - 顯示 c
步驟 5 - 停止
在演算法的設計和分析中,通常使用第二種方法來描述演算法。它使分析師能夠輕鬆地分析演算法,而忽略所有不需要的定義。他可以觀察正在使用的操作以及流程是如何流動的。
編寫步驟編號是可選的。
我們設計算法來獲得給定問題的解決方案。一個問題可以透過多種方式解決。
因此,對於給定問題,可以推匯出許多解決方案演算法。下一步是分析這些提出的解決方案演算法並實現最合適的解決方案。
Python - 分治法
在分治法中,手頭的難題被分解成更小的子問題,然後每個問題都獨立解決。當我們繼續將子問題分解成更小的子問題時,我們最終可能會達到無法再進行分解的階段。這些“原子”最小的子問題(部分)得到解決。最後合併所有子問題的解決方案,以獲得原始問題的解決方案。
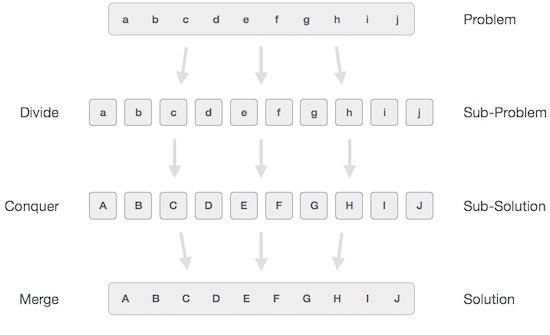
從廣義上講,我們可以將分治方法理解為一個三步過程。
分/分解
此步驟涉及將問題分解成更小的子問題。子問題應代表原始問題的一部分。此步驟通常採用遞迴方法來劃分問題,直到沒有子問題可以進一步劃分。在此階段,子問題變得具有原子性,但仍然代表實際問題的一部分。
解決/求解
此步驟接收大量需要解決的較小子問題。通常,在此級別,問題被認為是“自行解決”的。
合併/組合
當較小子問題得到解決時,此階段遞迴地將它們組合起來,直到它們形成原始問題的解決方案。這種演算法方法以遞迴方式工作,並且解決和合並步驟非常接近,以至於它們看起來像一個。
示例
以下程式是分治程式設計方法的一個示例,其中使用 Python 實現二分查詢。
二分查詢實現
在二分查詢中,我們取一個排序的元素列表,並從列表中間開始查詢元素。如果搜尋值與列表中的中間值匹配,則我們完成搜尋。否則,我們透過選擇繼續處理列表的右側或左側一半來消除一半的元素列表,具體取決於搜尋專案的價值。
這是可能的,因為列表已排序,並且比線性搜尋快得多。在這裡,我們劃分給定的列表並透過選擇列表的適當一半來征服。我們重複此方法,直到找到元素或得出關於其在列表中不存在的結論。
示例
def bsearch(list, val):
list_size = len(list) - 1
idx0 = 0
idxn = list_size
# Find the middle most value
while idx0 <= idxn:
midval = (idx0 + idxn)// 2
if list[midval] == val:
return midval
# Compare the value the middle most value
if val > list[midval]:
idx0 = midval + 1
else:
idxn = midval - 1
if idx0 > idxn:
return None
# Initialize the sorted list
list = [2,7,19,34,53,72]
# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))
輸出
當執行上述程式碼時,它會產生以下結果:
5 None
Python - 遞迴
遞迴允許函式呼叫自身。程式碼的固定步驟會針對新值重複執行。我們還必須設定標準來決定遞迴呼叫何時結束。在下面的示例中,我們看到了二分查詢的遞迴方法。我們取一個排序的列表,並將其索引範圍作為輸入提供給遞迴函式。
使用遞迴的二分查詢
我們使用 Python 實現二分查詢演算法,如下所示。我們使用一個有序的專案列表,並設計一個遞迴函式,以列表以及起始和結束索引作為輸入。然後,二分查詢函式會自行呼叫,直到找到搜尋的專案或得出關於其在列表中不存在的結論。
示例
def bsearch(list, idx0, idxn, val):
if (idxn < idx0):
return None
else:
midval = idx0 + ((idxn - idx0) // 2)
# Compare the search item with middle most value
if list[midval] > val:
return bsearch(list, idx0, midval-1,val)
else if list[midval] < val:
return bsearch(list, midval+1, idxn, val)
else:
return midval
list = [8,11,24,56,88,131]
print(bsearch(list, 0, 5, 24))
print(bsearch(list, 0, 5, 51))
輸出
當執行上述程式碼時,它會產生以下結果:
2 None
Python - 回溯法
回溯是一種遞迴形式。但它只涉及從任何可能性中選擇一個選項。我們首先選擇一個選項,如果我們到達一個狀態,我們得出結論,這個特定選項沒有給出所需的解決方案,則從該選項回溯。我們透過遍歷每個可用選項重複這些步驟,直到我們獲得所需的解決方案。
下面是一個查詢給定字母集的所有可能的排列順序的示例。當我們選擇一對時,我們應用回溯來驗證該確切的對是否已建立。如果尚未建立,則將該對新增到答案列表中,否則將其忽略。
示例
def permute(list, s):
if list == 1:
return s
else:
return [
y + x
for y in permute(1, s)
for x in permute(list - 1, s)
]
print(permute(1, ["a","b","c"]))
print(permute(2, ["a","b","c"]))
輸出
當執行上述程式碼時,它會產生以下結果:
['a', 'b', 'c'] ['aa', 'ab', 'ac', 'ba', 'bb', 'bc', 'ca', 'cb', 'cc']
Python - 排序演算法
排序是指以特定格式排列資料。排序演算法指定以特定順序排列資料的方式。最常見的順序是按數字或字典順序。
排序的重要性在於,如果資料以排序的方式儲存,則可以將資料搜尋最佳化到非常高的水平。排序還用於以更易讀的格式表示資料。下面我們看到五種在 Python 中實現排序的方法。
氣泡排序
歸併排序
插入排序
希爾排序
選擇排序
氣泡排序
這是一種基於比較的演算法,其中比較每對相鄰元素,如果不按順序排列,則交換元素。
示例
def bubblesort(list):
# Swap the elements to arrange in order
for iter_num in range(len(list)-1,0,-1):
for idx in range(iter_num):
if list[idx]>list[idx+1]:
temp = list[idx]
list[idx] = list[idx+1]
list[idx+1] = temp
list = [19,2,31,45,6,11,121,27]
bubblesort(list)
print(list)
輸出
當執行上述程式碼時,它會產生以下結果:
[2, 6, 11, 19, 27, 31, 45, 121]
歸併排序
歸併排序首先將陣列分成相等的兩半,然後以排序的方式將它們組合起來。
示例
def merge_sort(unsorted_list):
if len(unsorted_list) <= 1:
return unsorted_list
# Find the middle point and devide it
middle = len(unsorted_list) // 2
left_list = unsorted_list[:middle]
right_list = unsorted_list[middle:]
left_list = merge_sort(left_list)
right_list = merge_sort(right_list)
return list(merge(left_list, right_list))
# Merge the sorted halves
def merge(left_half,right_half):
res = []
while len(left_half) != 0 and len(right_half) != 0:
if left_half[0] < right_half[0]:
res.append(left_half[0])
left_half.remove(left_half[0])
else:
res.append(right_half[0])
right_half.remove(right_half[0])
if len(left_half) == 0:
res = res + right_half
else:
res = res + left_half
return res
unsorted_list = [64, 34, 25, 12, 22, 11, 90]
print(merge_sort(unsorted_list))
輸出
當執行上述程式碼時,它會產生以下結果:
[11, 12, 22, 25, 34, 64, 90]
插入排序
插入排序包括在已排序列表中找到給定元素的正確位置。因此,在開始時,我們比較前兩個元素並透過比較它們來排序。然後我們選擇第三個元素,並在前兩個已排序元素中找到其正確位置。這樣,我們逐漸繼續將更多元素新增到已排序列表中,方法是將它們放在其正確的位置。
示例
def insertion_sort(InputList):
for i in range(1, len(InputList)):
j = i-1
nxt_element = InputList[i]
# Compare the current element with next one
while (InputList[j] > nxt_element) and (j >= 0):
InputList[j+1] = InputList[j]
j=j-1
InputList[j+1] = nxt_element
list = [19,2,31,45,30,11,121,27]
insertion_sort(list)
print(list)
輸出
當執行上述程式碼時,它會產生以下結果:
[19, 2, 31, 45, 30, 11, 27, 121]
希爾排序
希爾排序涉及對彼此遠離的元素進行排序。我們對給定列表的大子列表進行排序,並繼續減小子列表的大小,直到所有元素都排序。下面的程式透過將其與列表大小長度的一半相等來找到間隔,然後開始對其中的所有元素進行排序。然後我們繼續重置間隔,直到整個列表排序。
示例
def shellSort(input_list):
gap = len(input_list) // 2
while gap > 0:
for i in range(gap, len(input_list)):
temp = input_list[i]
j = i
# Sort the sub list for this gap
while j >= gap and input_list[j - gap] > temp:
input_list[j] = input_list[j - gap]
j = j-gap
input_list[j] = temp
# Reduce the gap for the next element
gap = gap//2
list = [19,2,31,45,30,11,121,27]
shellSort(list)
print(list)
輸出
當執行上述程式碼時,它會產生以下結果:
[2, 11, 19, 27, 30, 31, 45, 121]
選擇排序
在選擇排序中,我們首先在給定列表中找到最小值,並將其移動到已排序列表。然後我們對無序列表中每個剩餘元素重複此過程。進入已排序列表的下一個元素與現有元素進行比較,並放置在其正確的位置。因此,最後所有來自無序列表的元素都已排序。
示例
def selection_sort(input_list):
for idx in range(len(input_list)):
min_idx = idx
for j in range( idx +1, len(input_list)):
if input_list[min_idx] > input_list[j]:
min_idx = j
# Swap the minimum value with the compared value
input_list[idx], input_list[min_idx] = input_list[min_idx], input_list[idx]
l = [19,2,31,45,30,11,121,27]
selection_sort(l)
print(l)
輸出
當執行上述程式碼時,它會產生以下結果:
[19, 2, 31, 45, 30, 11, 121, 27]
Python - 搜尋演算法
當您將資料儲存在不同的資料結構中時,搜尋是一個非常基本的需求。最簡單的方法是遍歷資料結構中的每個元素,並將其與您要搜尋的值進行匹配。這稱為線性搜尋。它效率低下且很少使用,但為此建立程式可以讓我們瞭解如何實現一些高階搜尋演算法。
線性搜尋
在這種型別的搜尋中,對所有專案依次進行順序搜尋。檢查每個專案,如果找到匹配項,則返回該特定專案,否則搜尋將繼續到資料結構的末尾。
示例
def linear_search(values, search_for):
search_at = 0
search_res = False
# Match the value with each data element
while search_at < len(values) and search_res is False:
if values[search_at] == search_for:
search_res = True
else:
search_at = search_at + 1
return search_res
l = [64, 34, 25, 12, 22, 11, 90]
print(linear_search(l, 12))
print(linear_search(l, 91))
輸出
當執行上述程式碼時,它會產生以下結果:
True False
插值搜尋
此搜尋演算法基於所需值的探測位置。為了使此演算法正常工作,資料集合應以排序形式且均勻分佈。最初,探測位置是集合中最中間專案的的位置。如果發生匹配,則返回專案的索引。如果中間專案大於該專案,則在中間專案右側的子陣列中再次計算探測位置。否則,在中間專案左側的子陣列中搜索該專案。此過程也繼續在子陣列上進行,直到子陣列的大小減小到零。
示例
有一個特定的公式來計算中間位置,如下面的程式所示。
def intpolsearch(values,x ):
idx0 = 0
idxn = (len(values) - 1)
while idx0 <= idxn and x >= values[idx0] and x <= values[idxn]:
# Find the mid point
mid = idx0 +\
int(((float(idxn - idx0)/( values[idxn] - values[idx0]))
* ( x - values[idx0])))
# Compare the value at mid point with search value
if values[mid] == x:
return "Found "+str(x)+" at index "+str(mid)
if values[mid] < x:
idx0 = mid + 1
return "Searched element not in the list"
l = [2, 6, 11, 19, 27, 31, 45, 121]
print(intpolsearch(l, 2))
輸出
當執行上述程式碼時,它會產生以下結果:
Found 2 at index 0
Python - 圖演算法
圖是在解決許多重要的數學挑戰時非常有用的資料結構。例如,計算機網路拓撲或分析化學化合物的分子結構。它們還用於城市交通或路線規劃,甚至用於人類語言及其語法。所有這些應用程式都面臨著一個共同的挑戰,即使用其邊遍歷圖並確保訪問圖的所有節點。有兩種常用的方法可以執行此遍歷,如下所述。
深度優先遍歷
也稱為深度優先搜尋 (DFS),此演算法以深度方向遍歷圖,並使用堆疊來記住在任何迭代中發生死鎖時開始搜尋的下一個頂點。我們使用集合資料型別在 Python 中為圖實現 DFS,因為它們提供了跟蹤已訪問和未訪問節點所需的函式。
示例
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
# Check for the visisted and unvisited nodes
def dfs(graph, start, visited = None):
if visited is None:
visited = set()
visited.add(start)
print(start)
for next in graph[start] - visited:
dfs(graph, next, visited)
return visited
gdict = {
"a" : set(["b","c"]),
"b" : set(["a", "d"]),
"c" : set(["a", "d"]),
"d" : set(["e"]),
"e" : set(["a"])
}
dfs(gdict, 'a')
輸出
當執行上述程式碼時,它會產生以下結果:
a b d e c
廣度優先遍歷
也稱為廣度優先搜尋 (BFS),此演算法以廣度方向遍歷圖,並使用佇列來記住在任何迭代中發生死鎖時開始搜尋的下一個頂點。請訪問我們網站中的此連結以瞭解圖的 BFS 步驟的詳細資訊。
我們使用前面討論的佇列資料結構在 Python 中為圖實現 BFS。當我們繼續訪問相鄰的未訪問節點並將其新增到佇列中時。然後我們僅開始出隊沒有未訪問節點的節點。當沒有下一個要訪問的相鄰節點時,我們停止程式。
示例
import collections
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def bfs(graph, startnode):
# Track the visited and unvisited nodes using queue
seen, queue = set([startnode]), collections.deque([startnode])
while queue:
vertex = queue.popleft()
marked(vertex)
for node in graph[vertex]:
if node not in seen:
seen.add(node)
queue.append(node)
def marked(n):
print(n)
# The graph dictionary
gdict = {
"a" : set(["b","c"]),
"b" : set(["a", "d"]),
"c" : set(["a", "d"]),
"d" : set(["e"]),
"e" : set(["a"])
}
bfs(gdict, "a")
輸出
當執行上述程式碼時,它會產生以下結果:
a c b d e
Python - 演算法分析
可以在兩個不同的階段分析演算法的效率,即實現之前和實現之後。它們如下所述。
先驗分析 - 這是對演算法的理論分析。透過假設所有其他因素(例如處理器速度)都是恆定的並且對實現沒有影響來衡量演算法的效率。
後驗分析 - 這是對演算法的經驗分析。使用程式語言實現所選演算法。然後在目標計算機上執行此操作。在此分析中,收集實際統計資訊,例如執行時間和所需空間。
演算法複雜度
假設X是一個演算法,n是輸入資料的大小,演算法 X 使用的時間和空間是決定 X 效率的兩個主要因素。
時間因素 - 透過計算關鍵操作的數量(例如排序演算法中的比較)來衡量時間。
空間因素 - 透過計算演算法所需的最大記憶體空間來衡量空間。
演算法f(n)的複雜度以n(作為輸入資料的大小)給出演算法的執行時間和/或儲存空間。
空間複雜度
演算法的空間複雜度表示演算法在其生命週期中所需的記憶體空間量。演算法所需的空間等於以下兩個元件的總和。
一個固定部分,即用於儲存某些資料和變數的空間,這些資料和變數與問題的規模無關。例如,使用的簡單變數和常量、程式大小等。
一個可變部分,即由變數所需的空間,其大小取決於問題的規模。例如,動態記憶體分配、遞迴堆疊空間等。
任何演算法 P 的空間複雜度 S(P) 為 S(P) = C + SP(I),其中 C 是固定部分,S(I) 是演算法的可變部分,它取決於例項特徵 I。以下是一個簡單的示例,試圖解釋這個概念。
演算法:SUM(A, B)
步驟 1 - 開始
步驟 2 - C ← A + B + 10
步驟 3 - 停止
這裡我們有三個變數 A、B 和 C 以及一個常量。因此 S(P) = 1 + 3。現在,空間取決於給定變數和常量型別的資料型別,並且將相應地乘以它。
時間複雜度
演算法的時間複雜度表示演算法執行到完成所需的時間量。時間需求可以定義為數值函式 T(n),其中 T(n) 可以衡量為步驟數,前提是每個步驟消耗恆定時間。
例如,兩個 n 位整數的加法需要n個步驟。因此,總計算時間為 T(n) = c ∗ n,其中 c 是兩個位加法所需的時間。在這裡,我們觀察到 T(n) 隨著輸入大小的增加而線性增長。
Python - 演算法型別
必須分析演算法的效率和準確性才能比較它們並在某些情況下選擇特定的演算法。進行此分析的過程稱為漸近分析。它指的是用數學計算單位計算任何操作的執行時間。
例如,一個操作的執行時間計算為 f(n),另一個操作的執行時間計算為 g(n2)。這意味著第一個操作的執行時間將隨著 n 的增加而線性增加,而第二個操作的執行時間將在 n 增加時呈指數增長。同樣,如果 n 非常小,則兩個操作的執行時間將幾乎相同。
通常,演算法所需的時間分為三種類型。
最佳情況 - 程式執行所需的最小時間。
平均情況 - 程式執行所需的平均時間。
最壞情況 - 程式執行所需的最大時間。
漸近表示法
常用的漸近表示法來計算演算法的執行時間複雜度。
Ο 表示法
Ω 表示法
θ 表示法
大 O 表示法,Ο
Ο(n) 表示法是表達演算法執行時間上界的正式方法。它衡量最壞情況時間複雜度或演算法可能完成所需的最長時間。

例如,對於函式f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
Omega 表示法,Ω
Ω(n) 表示法是表達演算法執行時間下界的正式方法。它衡量最佳情況時間複雜度或演算法可能完成所需的最短時間。
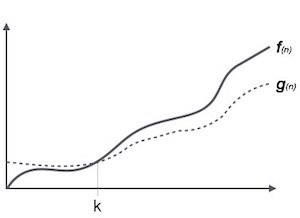
例如,對於函式f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
Theta 表示法,θ
θ(n) 表示法是表達演算法執行時間下界和上界的正式方法。它表示如下。
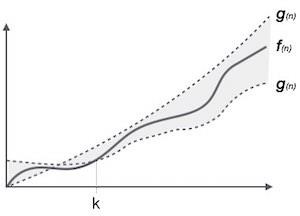
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
常用漸近表示法
下面列出了一些常用的漸近表示法。
| 常數 | — | Ο(1) |
| 對數 | — | Ο(log n) |
| 線性 | — | Ο(n) |
| n log n | — | Ο(n log n) |
| 二次 | — | Ο(n2) |
| 三次 | — | Ο(n3) |
| 多項式 | — | nΟ(1) |
| 指數 | — | 2Ο(n) |
Python - 演算法類別
演算法是不明確的步驟,應該透過處理零個或多個輸入來為我們提供明確的輸出。這導致了在設計和編寫演算法方面的許多方法。據觀察,大多數演算法可以分為以下幾類。
貪心演算法
貪婪演算法試圖找到區域性最優解,這最終可能導致全域性最優解。但是,通常貪婪演算法並不能提供全域性最優解。
因此,貪婪演算法在那個時間點尋找一個簡單的解決方案,而不考慮它如何影響未來的步驟。這類似於人類在沒有完全瞭解所提供輸入的情況下解決問題的方式。
大多數網路演算法都使用貪婪方法。以下是一些示例:
旅行商問題
Prim 最小生成樹演算法
Kruskal 最小生成樹演算法
Dijkstra 最小生成樹演算法
分治法
這類演算法涉及將給定問題分解成更小的子問題,然後獨立地解決每個子問題。當問題無法進一步細分時,我們開始合併每個子問題的解決方案,以得出更大問題的解決方案。
分治演算法的重要示例包括:
歸併排序
快速排序
Kruskal 最小生成樹演算法
二分查詢
動態規劃
動態規劃也涉及將更大的問題分解成更小的子問題,但與分治法不同,它不涉及獨立地解決每個子問題。相反,它會記住較小子問題的結果,並在類似或重疊的子問題中使用它們。
通常,這些演算法用於最佳化。在解決手頭的子問題之前,動態演算法會嘗試檢查先前解決的子問題的結果。動態演算法的目的是對問題進行整體最佳化,而不是區域性最佳化。
動態規劃演算法的重要示例包括:
斐波那契數列
揹包問題
漢諾塔
Python - 均攤分析
攤還分析涉及估計程式中一系列操作的執行時間,而不考慮輸入值中資料分佈的範圍。一個簡單的例子是在排序列表中查詢值比在未排序列表中查詢值更快。
如果列表已排序,則資料分佈方式無關緊要。但當然,列表的長度會產生影響,因為它決定了演算法必須經歷多少步驟才能獲得最終結果。
因此,我們看到,如果獲得排序列表的單個步驟的初始成本很高,則隨後查詢元素的步驟的成本會大大降低。因此,攤還分析有助於我們找到一系列操作的最壞情況執行時間的界限。攤還分析有三種方法。
會計方法 - 這涉及為執行的每個操作分配一個成本。如果實際操作完成得比分配的時間快,則分析中會累積一些正信用。
勢能方法 - 在這種方法中,儲存的信用作為資料結構狀態的數學函式用於將來的操作。數學函式的評估和攤還成本應該相等。因此,當實際成本大於攤還成本時,勢能會下降,並用於利用未來成本較高的操作。
聚合分析 - 在這種方法中,我們估計 n 步總成本的上限。攤還成本是總成本除以步數 (n) 的簡單除法。
在相反的情況下,它將是負信用。為了跟蹤這些累積的信用,我們使用堆疊或樹資料結構。早期執行的操作(如排序列表)具有較高的攤還成本,但序列中較晚的操作具有較低的攤還成本,因為累積的信用被利用了。因此,攤還成本是實際成本的上限。
Python - 演算法論證
為了斷言某個演算法是高效的,我們需要一些數學工具作為證明。這些工具幫助我們對演算法的效能和準確性提供數學上令人滿意的解釋。下面列出了一些可用於證明一個演算法優於另一個演算法的數學工具。
直接證明 - 它透過使用直接計算來直接驗證陳述。例如,兩個偶數的和始終是偶數。在這種情況下,只需將您正在研究的兩個數字相加並驗證結果為偶數即可。
數學歸納法 - 在這裡,我們從一個特定的事實例項開始,然後將其推廣到所有可能屬於該事實的值。這種方法是採用一個經過驗證的事實案例,然後證明在相同給定條件下,它對於下一個案例也成立。例如,所有形式為 2n-1 的正數都是奇數。我們證明了它對於某個 n 值成立,然後證明它對於下一個 n 值也成立。這透過歸納證明建立了該陳述通常是正確的。
反證法 - 這種證明基於條件“如果非 A 蘊含非 B,則 A 蘊含 B”。一個簡單的例子是,如果 n 的平方是偶數,則 n 必須是偶數。因為如果 n 的平方不是偶數,則 n 不是偶數。
窮舉證明 - 這類似於直接證明,但它是透過分別訪問每個案例並證明每個案例來建立的。這種證明的一個例子是四色定理。