Python程式：計算彩色頂點正多邊形中等腰三角形的數量

假設我們有一個n邊的正多邊形，用大小為n的二進位制字串表示。頂點可以塗成藍色（0）或紅色（1）。它們按順時針方向著色。我們必須計算頂點為正多邊形頂點且顏色相同的等腰三角形的數量。

因此，如果輸入類似於polygon = "111010"，則輸出為2，因為

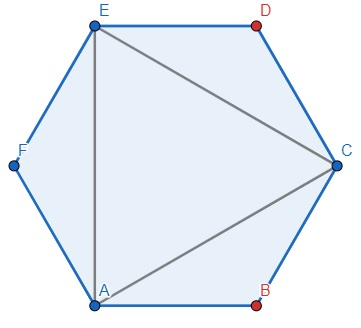
有兩個三角形ACE和AFE。

為了解決這個問題，我們將遵循以下步驟：

  • 定義一個函式all()。它將接收n。
  • 如果n mod 2等於1，則no := n*(n-1) /2
  • 否則，no := n*(n/2-1)
  • 如果n mod 3等於0，則no := no - n/3*2
  • 返回no
  • 定義一個函式non()。它將接收a,n。
  • 如果n mod 2等於1，則
    • s0 := 0, s1 := 0
    • i := 0
    • 當i < n時，執行：
      • 如果a[i]等於'0'，則s0 := s0 + 1
      • 否則s1 := s1 + 1
      • i := i + 1
    • s := s0*s1*6
    • 如果n mod 3等於0，則
      • n1 := n/3
      • n2 := n1*2
      • i := 0
      • 當i < n時，執行：
        • 如果a[i]不等於a[(i+n1)mod n]，則
          • s := s - 2
        • 如果a[i]不等於a[(i+n2)mod n]，則
          • s := s - 2
        • i := i + 1
  • 否則，
    • s00 := 0, s01 := 0, s10 := 0, s11 := 0, s := 0
    • i := 0
    • 當i < n時，執行：
      • 如果a[i]等於'0'，則s00 := s00 + 1
      • 否則s01 := s01 + 1
      • i := i + 2
    • i := 1
    • 當i < n時，執行：
      • 如果a[i]等於'0'，則s10 := s10 + 1
      • 否則s11 := s11 + 1
      • i := i + 2
    • s := s + s00 * s01 * 8
    • s := s + s10 * s11 * 8
    • s := s + s00 * s11 * 4
    • s := s + s10 * s01 * 4
    • n1 := n/2
    • i := 0
    • 當i < n時，執行：
      • 如果a[i]不等於a[(i + n1)mod n]，則
        • s := s - 2
      • i := i + 1
    • 如果n mod 3等於0，則
      • n1 := n/3
      • n2 := n1*2
      • i := 0
      • 當i < n時，執行：
        • 如果a[i]不等於a[(i+n1)mod n]，則
          • s := s - 2
        • 如果a[i]不等於a[(i+n2)mod n]，則
          • s := s - 2
        • i := i + 1
  • 返回s/2
  • 在主方法中，執行以下操作：
  • n := polygon的大小
  • no := all(n) - non(polygon, n) /2
  • 返回no

示例

讓我們來看下面的實現以更好地理解：

def all(n):
   if n % 2 == 1:
      no = n*(n-1)/2
   else:
      no = n*(n/2-1)
   if n % 3 == 0:
      no -= n/3*2
   return no

def non(a,n):
   if n % 2 == 1:
      s0 = s1 = 0
      i = 0
      while i < n:
         if a[i] == '0':
            s0 += 1
         else:
            s1 += 1
         i += 1
      s = s0*s1*6
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i<n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   else:
      s00 = s01 = s10 = s11 = s = 0
      i = 0
      while i <n:
         if a[i] == '0':
            s00 += 1
         else:
            s01 += 1
         i += 2
      i = 1
      while i < n:
         if a[i] == '0':
            s10 += 1
         else:
            s11 += 1
         i += 2
      s += s00 * s01 * 8
      s += s10 * s11 * 8
      s += s00 * s11 * 4
      s += s10 * s01 * 4
      n1 = n/2
      i = 0
      while i < n:
         if a[i] != a[int((i + n1)%n)]:
            s -= 2
         i += 1
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i < n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   return s/2

def solve(polygon):
   n = len(polygon)
   no = all(n) - non(polygon,n)/2
   return int(no)

polygon = "111010"
print(solve(polygon))

輸入

1, 1000

輸出

2

更新於：2021年10月11日

209 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始
廣告
© . All rights reserved.