
脈衝調製
到目前為止,我們已經討論了連續波調製。現在是離散訊號的時候了。脈衝調製技術處理離散訊號。讓我們看看如何將連續訊號轉換為離散訊號。稱為取樣的過程可以幫助我們做到這一點。
取樣
將連續時間訊號轉換為等效離散時間訊號的過程稱為取樣。在取樣過程中,持續取樣資料的某個瞬間。
下圖顯示了連續時間訊號x(t)和取樣訊號xs(t)。當x(t)乘以週期性脈衝序列時,得到取樣訊號xs(t)。
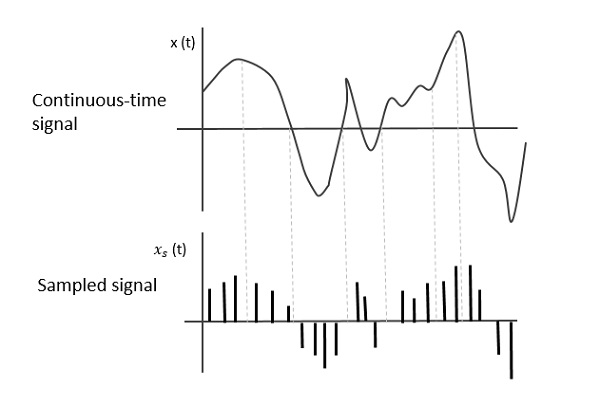
取樣訊號是脈衝的週期性序列,具有單位幅度,以相等的時間間隔Ts進行取樣,稱為取樣時間。這些資料在時間點Ts傳輸,載波訊號在剩餘時間傳輸。
取樣率
為了離散化訊號,樣本之間的間隙應固定。該間隙可以稱為取樣週期Ts。
$$取樣頻率 = \frac{1}{T_s} = f_s$$
其中,
Ts = 取樣時間
fs = 取樣頻率或採樣率
取樣定理
在考慮取樣率時,應該考慮一個關於該速率需要達到多少的重要問題。取樣率應使得訊息訊號中的資料既不會丟失也不會重疊。
取樣定理指出,“如果以fs速率對訊號進行取樣,該速率大於或等於最大頻率W的兩倍,則可以精確地重現該訊號。”
簡單來說,為了有效地重現原始訊號,取樣率應為最高頻率的兩倍。
這意味著,
$$f_s \geq 2W$$
其中,
fs = 取樣頻率
W 是最高頻率
此取樣率稱為奈奎斯特率。
取樣定理,也稱為奈奎斯特定理,根據頻寬為帶限函式類提供了足夠的取樣率理論。
對於連續時間訊號x(t),頻域中的帶限訊號可以表示如下面的圖所示。
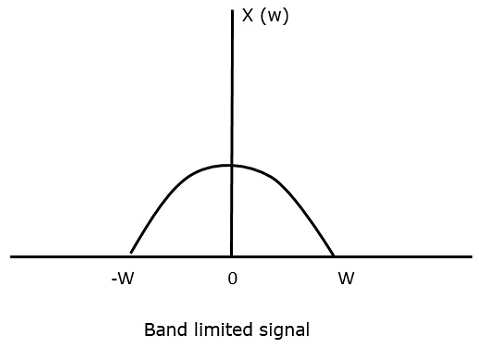
如果訊號以高於奈奎斯特率的速率取樣,則可以恢復原始訊號。下圖說明了如果在頻域中以高於2w的速率取樣訊號的情況。
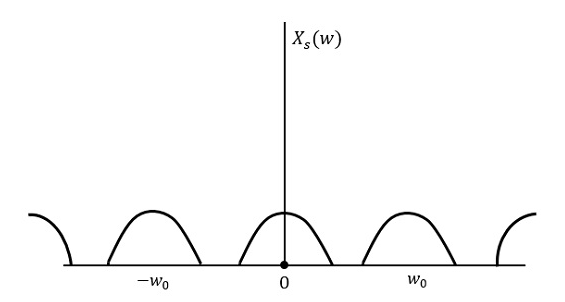
如果以低於2w的速率對同一訊號進行取樣,則取樣訊號將如下面的圖所示。
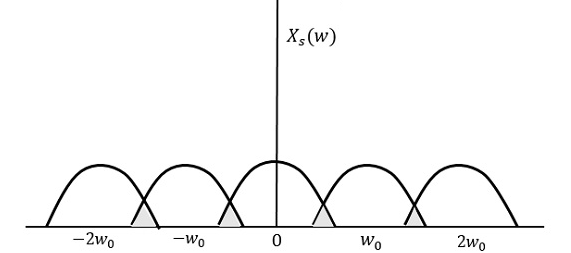
我們可以從上述模式中觀察到,資訊發生了重疊,這會導致資訊混合和丟失。這種不希望發生的重疊現象稱為混疊。
混疊可以指“訊號頻譜中高頻分量在其取樣版本的頻譜中呈現為低頻分量的現象。”
因此,選擇訊號的取樣率為奈奎斯特率,如取樣定理中所述。如果取樣率等於最高頻率的兩倍(2W)。
這意味著,
$$f_s = 2W$$
其中,
fs = 取樣頻率
W 是最高頻率
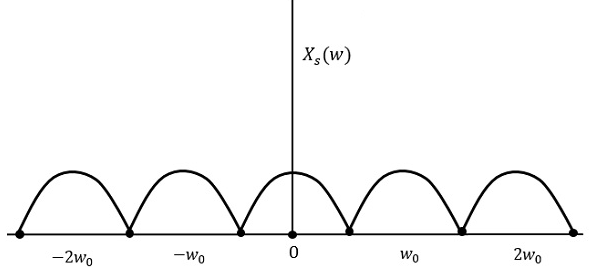
結果將如上圖所示。資訊被替換,沒有任何損失。因此,這是一個良好的取樣率。