
幅度調製
在各種調製技術中,主要分類為連續波調製和脈衝調製。連續波調製技術進一步細分為**幅度調製**和**角調製**。
連續波不斷地持續下去,沒有任何間隔,它是包含資訊的基帶訊息訊號。這個波需要進行調製。
根據標準定義,“載波訊號的幅度根據調製訊號的瞬時幅度變化。”這意味著,不包含資訊的載波訊號的幅度根據包含資訊的訊號的幅度在每個時刻發生變化。這可以透過下圖很好地解釋。
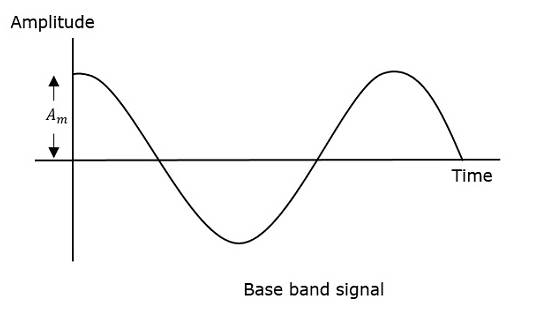
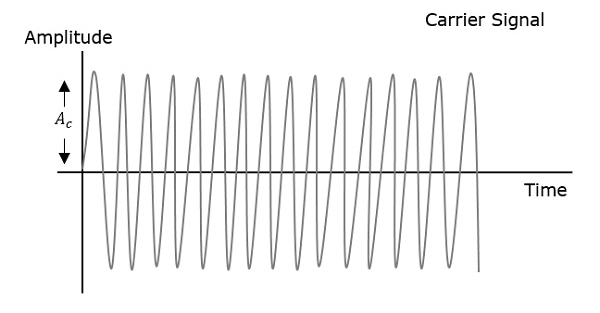
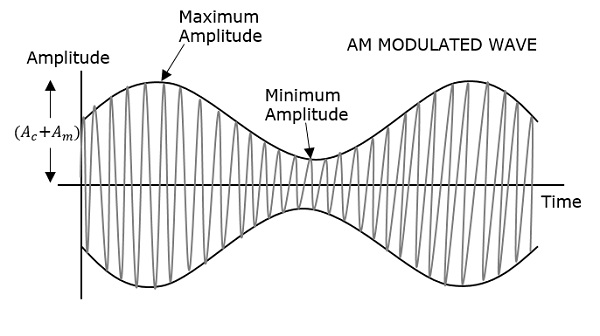
首先顯示的調製波是訊息訊號。下一個是載波,它只是一個高頻訊號,不包含任何資訊。而最後一個是所得的調製波。
可以觀察到,載波的正負峰值用一條假想線連線起來。這條線有助於重現調製訊號的精確形狀。載波上的這條假想線稱為**包絡線**。它與訊息訊號相同。
數學表示式
以下是這些波的數學表示式。
波的時間域表示
設調製訊號為 -
$$m(t) = A_mcos(2\pi f_mt)$$
設載波訊號為 -
$$c(t) = A_ccos(2\pi f_ct)$$
其中**Am** = 調製訊號的最大幅度
**Ac** = 載波訊號的最大幅度
幅度調製波的標準形式定義為 -
$$S(t) = A_c[1+K_am(t)]cos(2\pi f_ct)$$
$$S(t) = A_c[1+\mu cos(2\pi f_mt)]cos(2\pi f_ct)$$
$$其中,\mu = K_aA_m$$
調製指數
載波在被調製後,如果計算調製電平,則這種嘗試稱為**調製指數**或**調製深度**。它表示載波所經歷的調製程度。
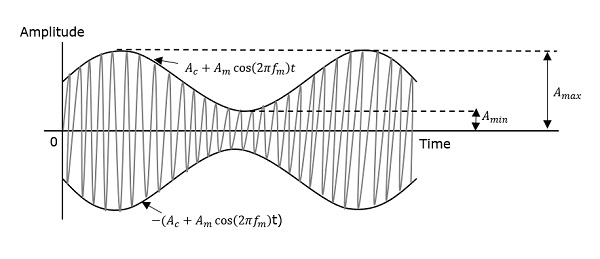
調製波包絡線的最大值和最小值分別用Amax和Amin表示。
讓我們嘗試為調製指數推匯出一個方程。
$$A_{max} = A_c(1+\mu )$$
因為,在Amax處,cos θ的值為1
$$A_{min} = A_c(1-\mu )$$
因為,在Amin處,cos θ的值為-1
$$\frac{A_{max}}{A_{min}} = \frac{1+\mu }{1-\mu }$$
$$A_{max}-\mu A_{max} = A_{min}+\mu A_{min}$$
$$-\mu (A_{max}+A_{min}) = A_{min}-A_{max}$$
$$\mu = \frac{A_{max}-A_{min}}{A_{max}+A_{min}}$$
因此,得到了調製指數的方程。µ表示調製指數或調製深度。這通常以百分比表示,稱為**調製百分比**。它是以百分比表示的調製程度,用m表示。
對於完美的調製,調製指數的值應為1,這意味著調製深度應為100%。
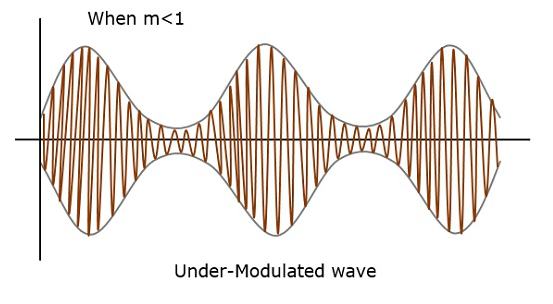
例如,如果此值小於1,即調製指數為0.5,則調製輸出將類似於下圖。這稱為欠調製。這種波稱為**欠調波**。
如果調製指數的值大於1,例如1.5左右,則該波將成為**過調波**。它將類似於下圖。
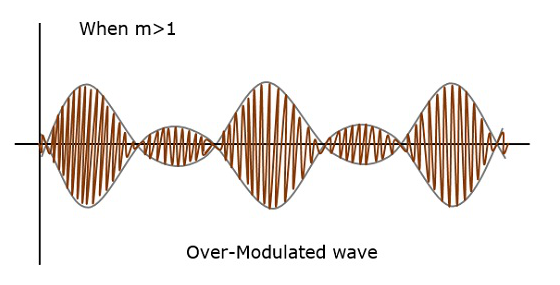
隨著調製指數值的增加,載波會經歷180°的相位反轉,這會導致額外的邊帶,因此波形會失真。這種過調波會導致干擾,無法消除。
幅度調製的頻寬
頻寬是指訊號的最低頻率和最高頻率之間的差值。
對於幅度調製波,頻寬由下式給出
$$BW = f_{USB}-f_{LSB}$$
$$(f_c+f_m)-(f_c-f_m)$$
$$ = 2f_m = 2W$$
其中**W**是訊息頻寬
因此,我們瞭解到幅度調製波所需的頻寬是調製訊號頻率的兩倍。