資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究Potier三角形法 - 確定同步發電機的電壓調整
Potier三角形法用於確定同步發電機的電壓調整。它也稱為零功率因數 (ZPF) 法。在Potier三角形法中做出了以下假設：
電樞反應磁動勢是恆定的。
空載時測得的開路特性 (O.C.C.) 精確地表示了負載條件下磁動勢和電壓之間的關係。
電樞漏抗引起的電壓降 ($𝐼_{𝑎}𝑋_{𝑎𝐿}$) 與勵磁無關。
使用 ZPF 方法獲取電壓調整的程式
以下是使用零功率因數 (ZPF) 方法確定同步發電機或交流發電機電壓調整的程式：
首先，我們繪製同步發電機在滯後功率因數下的相量圖，如圖所示。
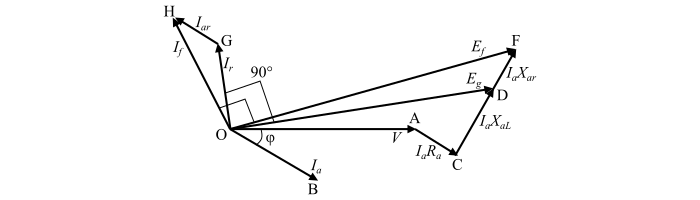
在相量圖中，
相量 OA 表示滿載時的端相電壓 (V)。它被視為參考相量，因此水平繪製。
相量 OB 表示滿載電流 ($𝐼_{𝑎}$)。由於負載功率因數為 φ 滯後，因此它以功率因數角 (φ) 滯後於電壓 (V) 繪製。
相量 AC 表示電樞電阻中的電壓降 ($𝐼_{𝑎}𝑅_{𝑎}$)。由於它與電樞電流 ($𝐼_{𝑎}$) 同相，因此平行於電流相量 ($𝐼_{𝑎}$) 繪製。如果忽略電樞電阻，則該相量將不會在相量圖中繪製。
由於漏抗引起的電壓降 ($𝐼_{𝑎}𝑋_{𝑎𝐿}$) 由相量 CD 表示。它垂直於相量 AC。
現在，連線 O 和 D，相量 OD 表示感應電動勢 ($𝐸_{𝑔}$)。
現在，從開路特性 (O.C.C.) 中找到對應於感應電動勢 ($𝐸_{𝑔}$) 的合成磁動勢的勵磁電流 ($𝐼_{𝑟}$)。然後，繪製等於電流 ($𝐼_{𝑟}$) 的相量 OG，它垂直於相量 OD。
繪製平行於負載電流 ($𝐼_{𝑎}$) 的相量 GH，以表示等效於滿載電樞反應電流 ($𝐼_{a𝑟}$) 的勵磁電流。因此，相量 OH 給出了總勵磁電流 ($𝐼_{𝑓}$)。
當同步發電機的負載斷開時，端電壓將等於對應於勵磁電流 ($𝐼_{𝑓} = 𝑂𝐻$) 的感應電動勢。
現在，從 O.C.C. 中確定對應於勵磁電流 ($𝐼_{𝑓} = 𝑂𝐻$) 的相量 OF 所表示的電動勢 ($𝐸_{𝑓}$)。相量 OF 將滯後於相量 OH 90°。此外，由於電樞反應引起的電壓降由相量 DF 表示。
因此，同步發電機或交流發電機的電壓調整可以透過以下表達式獲得：
$$\mathrm{\%\:電壓調整 =\frac{𝐸_{𝑓} − 𝑉}{𝑉} \times 100}$$
7K+ 次檢視
