資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學變壓器電壓降近似值和變壓器電壓調整率
變壓器電壓降近似值
圖示為實際變壓器折算到副邊上的近似等效電路。
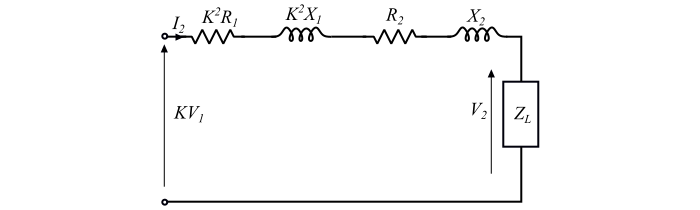
空載時，即 I2= 0，副邊端電壓為：
$$\mathrm{V_{2}=KV_{1} .....(1)}$$
當連線功率因數為 cosφ2（滯後）的感性負載到變壓器的副繞組時，副繞組流過電流 I2，因此在 $(R_{2} + K^2R_{1})$ 和 $(X_{2} + K^2X_{1})$ 上產生電壓降。結果，副邊電壓從 KV1 降到負載端子上的 V2。
根據基爾霍夫電壓定律 (KVL)，我們得到：
$$\mathrm{V_{2}=KV_{1}-I_{2}[(R_{2} + K^2R_{1})+J(X_{2} + K^2X_{1})]}$$
$$\mathrm{⇒ V_{2}=KV_{1}-I_{2}(R_{02} +jX_{02}) = KV_{1}-I_{2}Z_{02}}$$
因此，副邊電壓降為：
$$\mathrm{ KV_{1}-V_{2}=I_{2}Z_{02} .....(2)}$$
現在，參考相量圖，可以看出副邊電壓降為 $AC = I_{2}Z_{02}$，其計算方法如下：
以 O 為圓心，OC 為半徑，畫弧 OA 並延長至 M，則：
$$\mathrm{AC=AM \approx AN}$$
現在，從 B 作 BD 垂直於 OA，作 CN 垂直於 OM，作 BL 平行於 OM。因此，副邊電壓的近似降壓由下式給出：
$$\mathrm{副邊電壓近似降壓= AN = AD+DN}$$
$$\mathrm{\therefore \:BL = DN}$$
$$\mathrm{\because \:AN = AD + BL}$$
$$\mathrm{⇒ AN = I_{2}R_{02}\:cos\:\varphi _{2}\: + I_{2}X_{02}\:sin\:\varphi _{2} ....(3)}$$
公式 (3) 給出了滯後功率因數負載的副邊電壓近似降壓。
對於 *超前功率因數* 負載，變壓器的近似電壓降由下式給出：
$$\mathrm{近似電壓降\:=I_{2}R_{02}\:cos\:\varphi _{2}\:-\:I_{2}X_{02}\:sin\:\varphi _{2} ....(4)}$$
此外，如果變壓器電路折算到原邊，則
$$\mathrm{近似電壓降\:= I_{1}R_{01}\:cos\:\varphi_{1}\:±\:I_{1}X_{01}\:sin\:\varphi _{1} ....(5) }$$
由於原邊功率因數 (cos φ1) 和副邊功率因數 (cos φ2) 的值差異很小。因此，公式 (5) 也可以寫成
$$\mathrm{近似電壓降\:=\:I_{1}R_{01}\:cos\:\varphi _{2}\: ±\:I_{1}X_{01}\:sin\:\varphi _{2} ....(6)}$$
這裡，對於滯後功率因數負載使用正號，對於超前功率因數負載使用負號。
變壓器電壓調整率
變壓器的電壓調整率定義為空載副邊端電壓 (V2NL) 與滿載副邊端電壓 (V2FL) 之間的算術差，以給定功率因數下滿載（額定）副邊端電壓的百分比表示，原邊電壓在空載和滿載時保持恆定值，即
$$\mathrm{電壓調整率\:= \frac{V_{2NL}\:-\:V_{2FL}}{V_{2FL}}\:*100 ..... (7) }$$
從公式 (2) 可知，空載副邊端電壓為
$$V_{2NL} = KV_{1}$$
因此，變壓器從空載到滿載的電壓降由下式給出：
$$\mathrm{V_{2NL}\:-\:V_{2FL}\:=\: I_{2}R_{02}\:cos\:\varphi _{2}\:±\:I_{2}X_{02}\:sin\:\varphi _{2} .....(8)}$$
其中，滯後功率因數負載使用正號，超前功率因數負載使用負號。
$$\mathrm{\therefore\:電壓調整率\:=\:\frac{I_{2}R_{02}\:cos\:\varphi_{2}\:±\:I_{2}X_{02}\:sin\:\varphi _{2}}{V_{2FL}} ......(9)}$$
電壓調整率是衡量變壓器效能的指標。對於理想變壓器，電壓調整率為零。為了使變壓器更好地執行，電壓調整率應儘可能小。
對於變壓器，電壓變化的限值以電壓調整率的形式規定。例如，用於公共供電系統的變壓器的端電壓變化不得超過 ± 5%。
零電壓調整率的條件
考慮連線到變壓器上的感性負載，則變壓器的電壓調整率為
$$\mathrm{\therefore\:電壓調整率\:=\:\frac{I_{2}R_{02}\:cos\:\varphi _{2}\:+\:I_{2}X_{02}\:sin\:\varphi _{2}}{V_{2FL}} ..... (9)}$$
從這個表示式可以看出，當分子為零時，電壓調整率將為零，即
$$\mathrm{I_{2}R_{02}\:cos\:\varphi _{2}\:+\:I_{2}X_{02}\:sin\:\varphi_{2}= 0}$$
$$\mathrm{⇒\:tan\:\varphi_{2}\:=\:-\frac{R_{02}}{X_{02}}}$$
$$\mathrm{⇒\:\varphi_{2}\:=\:-tan^-1(\frac{R_{02}}{X_{02}}) .....(10)}$$
這裡，負號表示當負載為容性，即具有超前功率因數時，會發生零電壓調整率。
瀏覽量：1000+
