並行演算法 - 快速指南

---

---

並行演算法 - 簡介

演算法是一系列步驟，這些步驟接收使用者的輸入，經過一些計算後產生輸出。並行演算法是一種可以同時在不同的處理裝置上執行多個指令，然後組合所有單個輸出以產生最終結果的演算法。

併發處理

計算機的易用性以及網際網路的發展改變了我們儲存和處理資料的方式。我們生活在一個數據豐富且唾手可得的時代。每天我們都要處理大量需要複雜計算的資料，而且需要在短時間內完成。有時，我們需要從同時發生的類似或相關事件中提取資料。這就是我們需要併發處理的地方，它可以將複雜的任務分解並將其處理到多個系統中，以快速產生輸出。

當任務涉及處理大量複雜資料時，併發處理至關重要。例如 - 訪問大型資料庫、飛機測試、天文計算、原子和核物理、生物醫學分析、經濟計劃、影像處理、機器人技術、天氣預報、基於 Web 的服務等。

什麼是並行性？

並行性是同時處理多組指令的過程。它減少了總計算時間。並行性可以透過使用平行計算機來實現，即具有多個處理器的計算機。平行計算機需要支援多工的並行演算法、程式語言、編譯器和作業系統。

在本教程中，我們將僅討論並行演算法。在繼續之前，讓我們先討論演算法及其型別。

什麼是演算法？

演算法是為解決問題而遵循的一系列指令。在設計算法時，我們應該考慮演算法將在其上執行的計算機的體系結構。根據體系結構，計算機有兩種型別：

• 順序計算機
• 平行計算機

根據計算機的體系結構，我們有兩種型別的演算法：

• 順序演算法 - 其中一些連續的指令步驟按時間順序執行以解決問題。

• 並行演算法 - 問題被分解成子問題，並並行執行以獲得單個輸出。隨後，將這些單個輸出組合在一起以獲得最終所需的輸出。

將一個大問題分解成子問題並不容易。子問題之間可能存在資料依賴性。因此，處理器必須相互通訊才能解決問題。

研究發現，處理器之間進行通訊所需的時間多於實際處理時間。因此，在設計並行演算法時，應考慮適當的 CPU 利用率以獲得有效的演算法。

為了正確設計算法，我們必須清楚瞭解平行計算機中的基本計算模型。

計算模型

順序和平行計算機都操作一組（流）稱為演算法的指令。這組指令（演算法）指示計算機在每個步驟中必須做什麼。

根據指令流和資料流，計算機可以分為四類：

• 單指令流，單資料流 (SISD) 計算機
• 單指令流，多資料流 (SIMD) 計算機
• 多指令流，單資料流 (MISD) 計算機
• 多指令流，多資料流 (MIMD) 計算機

SISD 計算機

SISD 計算機包含一個控制單元、一個處理單元和一個儲存單元。

在這種型別的計算機中，處理器從控制單元接收單個指令流，並對來自儲存單元的單個數據流進行操作。在計算過程中，在每個步驟中，處理器從控制單元接收一條指令，並對從儲存單元接收的單個數據進行操作。

SIMD 計算機

SIMD 計算機包含一個控制單元、多個處理單元和共享記憶體或互連網路。

在這裡，一個控制單元將指令傳送到所有處理單元。在計算過程中，在每個步驟中，所有處理器都從控制單元接收一組指令，並對來自儲存單元的不同資料集進行操作。

每個處理單元都有自己的本地儲存單元來儲存資料和指令。在 SIMD 計算機中，處理器需要相互通訊。這是透過共享記憶體或互連網路完成的。

當一些處理器執行一組指令時，其餘處理器將等待下一組指令。來自控制單元的指令決定哪個處理器將處於活動狀態（執行指令）或處於非活動狀態（等待下一條指令）。

MISD 計算機

顧名思義，MISD 計算機包含多個控制單元、多個處理單元和一個公共儲存單元。

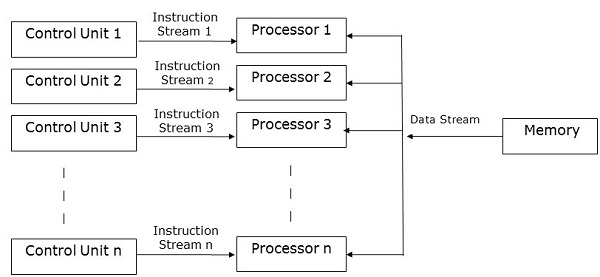
在這裡，每個處理器都有自己的控制單元，並且它們共享一個公共儲存單元。所有處理器都分別從其自己的控制單元獲取指令，並根據從各自控制單元接收的指令對單個數據流進行操作。此處理器同時執行。

MIMD 計算機

MIMD 計算機具有多個控制單元、多個處理單元和共享記憶體或互連網路。

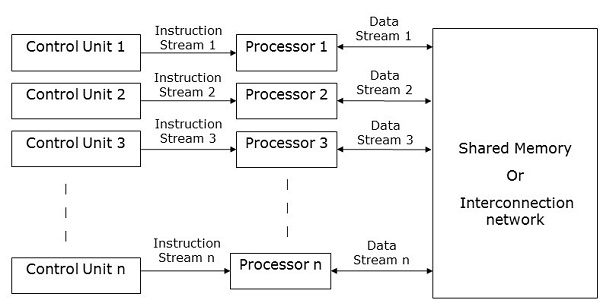
在這裡，每個處理器都有自己的控制單元、本地儲存單元以及算術和邏輯單元。它們從各自的控制單元接收不同的指令集，並對不同的資料集進行操作。

注意

• 共享公共記憶體的 MIMD 計算機稱為多處理器，而使用互連網路的計算機稱為多計算機。

• 根據處理器的物理距離，多計算機有兩種型別：

  • 多計算機 - 當所有處理器彼此非常靠近時（例如，在同一個房間裡）。

  • 分散式系統 - 當所有處理器彼此相距很遠時（例如，在不同的城市中）。

並行演算法 - 分析

演算法分析有助於我們確定演算法是否有用。通常，演算法的分析基於其執行時間（時間複雜度）和所需的空間量（空間複雜度）。

由於我們以合理的價格擁有先進的儲存裝置，因此儲存空間不再是一個問題。因此，空間複雜度沒有得到那麼多的重視。

並行演算法旨在提高計算機的計算速度。對於並行演算法的分析，我們通常考慮以下引數：

• 時間複雜度（執行時間），
• 使用的處理器總數，以及
• 總成本。

時間複雜度

開發並行演算法的主要原因是減少演算法的計算時間。因此，評估演算法的執行時間對於分析其效率至關重要。

執行時間是根據演算法解決問題所需的時間來衡量的。總執行時間是從演算法開始執行到停止執行的那一刻計算出來的。如果所有處理器並非同時開始或結束執行，則演算法的總執行時間是從第一個處理器開始執行的那一刻到最後一個處理器停止執行的那一刻。

演算法的時間複雜度可以分為三類：

• 最壞情況複雜度 - 當演算法對給定輸入所需的時間最多時。

• 平均情況複雜度 - 當演算法對給定輸入所需的時間平均時。

• 最佳情況複雜度 - 當演算法對給定輸入所需的時間最少時。

漸近分析

演算法的複雜度或效率是演算法執行以獲得所需輸出的步驟數。漸近分析用於在演算法的理論分析中計算演算法的複雜度。在漸近分析中，使用較長的輸入來計算演算法的複雜度函式。

注意 - 漸近是指一條線趨於與一條曲線相交，但它們不相交的條件。這裡直線和曲線彼此漸近。

漸近符號是使用速度的高界和低界來描述演算法最快和最慢可能執行時間的最簡單方法。為此，我們使用以下符號：

• 大 O 符號
• 歐米茄符號
• 西塔符號

大 O 符號

在數學中，大 O 符號用於表示函式的漸近特徵。它以簡單而準確的方法表示函式在大輸入下的行為。它是一種表示演算法執行時間上限的方法。它表示演算法完成執行可能花費的最長時間。函式 -

f(n) = O(g(n))

當且僅當存在正常數c和n₀使得f(n) ≤ c * g(n)對於所有n，其中n ≥ n₀。

歐米茄符號

歐米茄符號是表示演算法執行時間下限的一種方法。函式 -

f(n) = Ω (g(n))

如果存在正的常數c和n₀，使得對於所有n（其中n ≥ n₀）都有f(n) ≥ c * g(n)。

Theta 符號

Theta 符號是一種表示演算法執行時間下界和上界的方法。函式 −

f(n) = θ(g(n))

如果存在正的常數c₁, c₂, 和n₀，使得對於所有n（其中n ≥ n₀）都有c1 * g(n) ≤ f(n) ≤ c2 * g(n)。

演算法的加速比

並行演算法的效能透過計算其加速比來確定。加速比定義為特定問題最快已知順序演算法的最壞情況執行時間與並行演算法的最壞情況執行時間的比率。

使用的處理器數量

使用的處理器數量是分析並行演算法效率的一個重要因素。計算購買、維護和執行計算機的成本。演算法用來解決問題所使用的處理器越多，獲得的結果成本就越高。

總成本

並行演算法的總成本是時間複雜度和該特定演算法中使用的處理器數量的乘積。

總成本 = 時間複雜度 × 使用的處理器數量

因此，並行演算法的效率為 −

並行演算法 - 模型

並行演算法的模型是透過考慮資料劃分和處理方法的策略，並應用合適的策略來減少互動而開發的。在本章中，我們將討論以下並行演算法模型 −

• 資料並行模型
• 任務圖模型
• 工作池模型
• 主從模型
• 生產者-消費者或流水線模型
• 混合模型

資料並行

在資料並行模型中，任務被分配給程序，每個任務對不同的資料執行類似型別的操作。資料並行性是單個操作應用於多個數據項的結果。

資料並行模型可以應用於共享地址空間和訊息傳遞正規化。在資料並行模型中，可以透過選擇保留區域性性的分解、使用最佳化的集體互動例程或透過重疊計算和互動來減少互動開銷。

資料並行模型問題的首要特徵是資料並行性的強度隨著問題的規模而增加，這反過來使得可以使用更多程序來解決更大的問題。

示例 − 密集矩陣乘法。

任務圖模型

在任務圖模型中，並行性由任務圖表示。任務圖可以是平凡的或非平凡的。在這個模型中，利用任務之間的相關性來促進區域性性或最小化互動成本。這個模型被用來解決任務相關聯的資料量與任務相關的計算量相比非常大的問題。分配任務有助於改善任務之間資料移動的成本。

示例 − 並行快速排序、稀疏矩陣分解和透過分治法匯出的並行演算法。

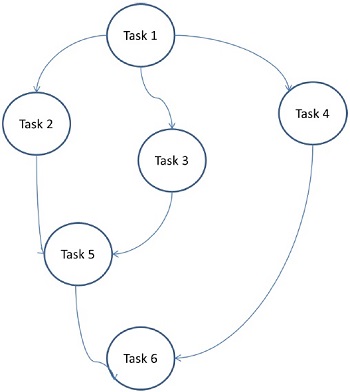
在這裡，問題被劃分為原子任務並實現為一個圖。每個任務都是一個獨立的作業單元，它依賴於一個或多個前置任務。任務完成後，前置任務的輸出將傳遞給依賴任務。只有在前置任務全部完成後，具有前置任務的任務才會開始執行。當最後一個依賴任務完成時（上圖中的任務 6），將收到圖的最終輸出。

工作池模型

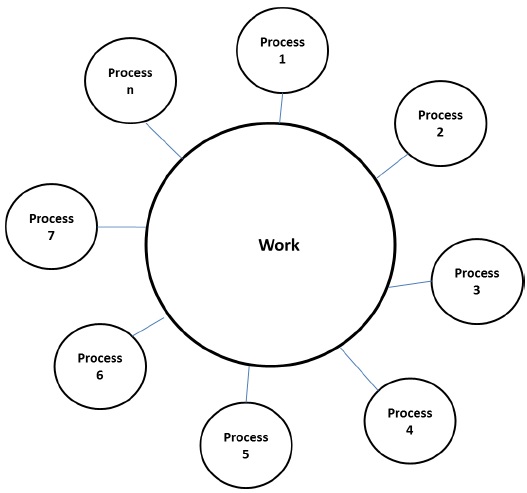
在工作池模型中，任務被動態分配給程序以平衡負載。因此，任何程序都可能執行任何任務。當與任務相關聯的資料量與任務相關的計算量相比相對較小時，使用此模型。

沒有預先將任務分配到程序的願望。任務的分配是集中式或分散式。指向任務的指標儲存在物理共享列表、優先順序佇列或雜湊表或樹中，或者它們可以儲存在物理分散式資料結構中。

任務可能在一開始就可用，也可能動態生成。如果任務是動態生成的並且任務的分配是分散式的，那麼需要一個終止檢測演算法，以便所有程序實際上都能檢測到整個程式的完成並停止尋找更多工。

示例 − 並行樹搜尋

主從模型

在主從模型中，一個或多個主程序生成任務並將其分配給從程序。如果以下情況，則可以預先分配任務 −

• 主程序可以估計任務量，或者
• 隨機分配可以很好地平衡負載，或者
• 從程序在不同時間被分配更小的任務片段。

此模型通常同樣適用於共享地址空間或訊息傳遞正規化，因為互動本質上是雙向的。

在某些情況下，任務可能需要分階段完成，並且每個階段的任務必須在下一個階段的任務生成之前完成。主從模型可以推廣到分層或多級主從模型，其中頂層主程序將大部分任務饋送到第二層主程序，後者進一步將任務細分給自己的從程序，並可能自行執行部分任務。

使用主從模型的注意事項

應注意確保主程序不會成為擁塞點。如果任務太小或工作程序相對較快，則可能會發生這種情況。

應以執行任務的成本超過通訊成本和同步成本的方式選擇任務。

非同步互動可能有助於重疊互動以及主程序生成工作相關的計算。

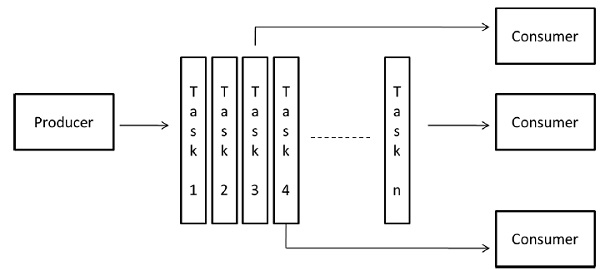
流水線模型

它也稱為生產者-消費者模型。這裡，一組資料透過一系列程序傳遞，每個程序對它執行某些任務。在這裡，新資料的到達會生成程序在佇列中執行新任務。這些程序可以形成線性或多維陣列、樹或具有或不具有迴圈的一般圖形狀的佇列。

此模型是生產者和消費者的鏈。佇列中的每個程序都可以被認為是佇列中前一個程序的一系列資料項的消費者，以及佇列中後一個程序的資料的生產者。佇列不需要是線性鏈；它可以是方向圖。適用於此模型的最常見的互動最小化技術是將互動與計算重疊。

示例 − 並行 LU 分解演算法。

混合模型

當需要多個模型來解決問題時，需要一個混合演算法模型。

混合模型可以由分層應用的多個模型或順序應用於並行演算法的不同階段的多個模型組成。

示例 − 並行快速排序

並行隨機存取機

並行隨機存取機 (PRAM) 是一個模型，它被認為適用於大多數並行演算法。在這裡，多個處理器連線到單個記憶體塊。PRAM 模型包含 −

• 一組相同型別的處理器。

• 所有處理器共享一個公共記憶體單元。處理器只能透過共享記憶體相互通訊。

• 一個記憶體訪問單元 (MAU) 將處理器與單個共享記憶體連線起來。

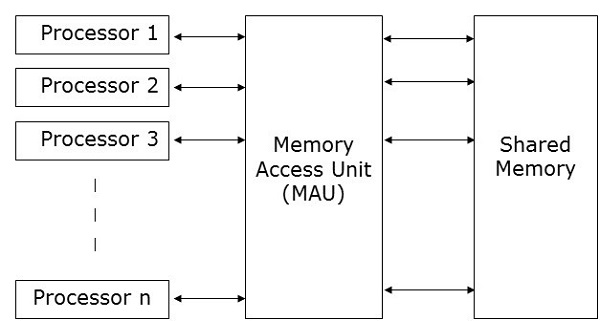
在這裡，n 個處理器可以在特定時間單位內對n 個數據執行獨立的操作。這可能會導致不同的處理器同時訪問相同的記憶體位置。

為了解決這個問題，對 PRAM 模型施加了以下約束 −

• 獨佔讀獨佔寫 (EREW) − 在這裡，不允許兩個處理器同時從同一記憶體位置讀取或寫入同一記憶體位置。

• 獨佔讀併發寫 (ERCW) − 在這裡，不允許兩個處理器同時從同一記憶體位置讀取，但允許它們同時寫入同一記憶體位置。

• 併發讀獨佔寫 (CREW) − 在這裡，允許所有處理器同時從同一記憶體位置讀取，但不允許它們同時寫入同一記憶體位置。

• 併發讀併發寫 (CRCW) − 允許所有處理器同時從同一記憶體位置讀取或寫入同一記憶體位置。

有許多方法可以實現 PRAM 模型，但最突出的方法是 −

• 共享記憶體模型
• 訊息傳遞模型
• 資料並行模型

共享記憶體模型

共享記憶體強調控制並行性而不是資料並行性。在共享記憶體模型中，多個程序在不同的處理器上獨立執行，但它們共享一個公共記憶體空間。由於任何處理器的活動，如果任何記憶體位置發生任何更改，則其他處理器都可以看到它。

由於多個處理器訪問相同的記憶體位置，因此在任何特定時間點，可能有多個處理器訪問相同的記憶體位置。假設一個正在讀取該位置，另一個正在寫入該位置。這可能會造成混淆。為了避免這種情況，實現了一些控制機制，如鎖/訊號量，以確保互斥。

共享記憶體程式設計已在以下方面實現 −

• 執行緒庫 − 執行緒庫允許多個控制執行緒在同一記憶體位置併發執行。執行緒庫提供了一個介面，透過一個子程式庫支援多執行緒。它包含用於以下方面的子程式

  • 建立和銷燬執行緒
  • 排程執行緒執行
  • 線上程之間傳遞資料和訊息
  • 儲存和恢復執行緒上下文

執行緒庫的示例包括 − SolarisTM 執行緒（適用於 Solaris）、POSIX 執行緒（在 Linux 中實現）、Win32 執行緒（在 Windows NT 和 Windows 2000 中可用）以及作為標準 JavaTM 開發工具包 (JDK) 一部分的 JavaTM 執行緒。

• 分散式共享記憶體 (DSM) 系統 − DSM 系統在鬆散耦合架構上建立共享記憶體的抽象，以便在沒有硬體支援的情況下實現共享記憶體程式設計。它們實現標準庫並使用現代作業系統中提供的先進使用者級記憶體管理功能。示例包括 Tread Marks 系統、Munin、IVY、Shasta、Brazos 和 Cashmere。

• 程式註釋包 − 這是在具有統一記憶體訪問特性的架構上實現的。程式註釋包最著名的示例是 OpenMP。OpenMP 實現功能並行性。它主要關注迴圈的並行化。

共享記憶體的概念提供了對共享記憶體系統的低階控制，但它往往很繁瑣且容易出錯。它更適用於系統程式設計而不是應用程式程式設計。

共享記憶體程式設計的優點

• 全域性地址空間為使用者提供了一種使用者友好的記憶體程式設計方法。

• 由於記憶體靠近 CPU，因此程序間的資料共享速度快且一致。

• 無需明確指定程序間的資料通訊。

• 程序通訊開銷可以忽略不計。

• 它很容易學習。

共享記憶體程式設計的缺點

• 它不可移植。
• 管理資料區域性性非常困難。

訊息傳遞模型

訊息傳遞是分散式記憶體系統中最常用的並行程式設計方法。在這裡，程式設計師必須確定並行性。在這個模型中，所有處理器都有自己的本地記憶體單元，並且它們透過通訊網路交換資料。

處理器使用訊息傳遞庫在它們之間進行通訊。除了傳送的資料外，訊息還包含以下元件：

• 傳送訊息的處理器的地址；

• 傳送處理器中資料的記憶體位置的起始地址；

• 傳送資料的型別；

• 傳送資料的大小；

• 傳送訊息的處理器的地址；

• 接收處理器中資料的記憶體位置的起始地址。

處理器可以透過以下任何一種方法相互通訊：

• 點對點通訊
• 集體通訊
• 訊息傳遞介面

點對點通訊

點對點通訊是最簡單的訊息傳遞形式。在這裡，可以透過以下任何一種傳輸模式將訊息從傳送處理器傳送到接收處理器：

• 同步模式 - 只有在收到確認其先前訊息已傳遞的確認後，才會傳送下一條訊息，以維護訊息的順序。

• 非同步模式 - 要傳送下一條訊息，不需要收到確認先前訊息已傳遞的確認。

集體通訊

集體通訊涉及多個處理器進行訊息傳遞。以下模式允許集體通訊：

• 屏障 - 如果參與通訊的所有處理器都執行一個特定的塊（稱為屏障塊）進行訊息傳遞，則屏障模式是可能的。

• 廣播 - 廣播有兩種型別：

  • 一對多 - 在這裡，一個處理器透過單個操作將相同的訊息傳送到所有其他處理器。

  • 全對全 - 在這裡，所有處理器都將訊息傳送到所有其他處理器。

廣播的訊息可能屬於三種類型：

• 個性化 - 將唯一的訊息傳送到所有其他目標處理器。

• 非個性化 - 所有目標處理器都接收相同的訊息。

• 歸約 - 在歸約廣播中，組中的一個處理器從組中的所有其他處理器收集所有訊息，並將它們組合成一個單一的訊息，組中的所有其他處理器都可以訪問該訊息。

訊息傳遞的優點

• 提供對並行性的低階控制；
• 它是可移植的；
• 錯誤率較低；
• 並行同步和資料分發中的開銷較少。

訊息傳遞的缺點

• 與並行共享記憶體程式碼相比，訊息傳遞程式碼通常需要更多的軟體開銷。

訊息傳遞庫

有很多訊息傳遞庫。在這裡，我們將討論兩個最常用的訊息傳遞庫：

• 訊息傳遞介面 (MPI)
• 並行虛擬機器 (PVM)

訊息傳遞介面 (MPI)

它是一個通用標準，用於在分散式記憶體系統中的所有併發程序之間提供通訊。大多數常用的平行計算平臺至少提供了一個訊息傳遞介面的實現。它已被實現為稱為庫的預定義函式的集合，並且可以從 C、C++、Fortran 等語言呼叫。與其他訊息傳遞庫相比，MPI 既快速又可移植。

訊息傳遞介面的優點

• 僅在共享記憶體體系結構或分散式記憶體體系結構上執行；

• 每個處理器都有自己的區域性變數；

• 與大型共享記憶體計算機相比，分散式記憶體計算機的成本更低。

訊息傳遞介面的缺點

• 並行演算法需要更多的程式設計更改；
• 有時難以除錯；並且
• 在節點之間的通訊網路中效能不佳。

並行虛擬機器 (PVM)

PVM 是一個可移植的訊息傳遞系統，旨在連線單獨的異構主機以形成單個虛擬機器。它是一種易於管理的平行計算資源。像超導研究、分子動力學模擬和矩陣演算法這樣的大型計算問題可以透過使用許多計算機的記憶體和總功率以更經濟有效的方式解決。它管理網路中不相容計算機體系結構的所有訊息路由、資料轉換和任務排程。

PVM 的特性

• 非常易於安裝和配置；
• 多個使用者可以同時使用 PVM；
• 一個使用者可以執行多個應用程式；
• 它是一個小軟體包；
• 支援 C、C++、Fortran；
• 對於給定的 PVM 程式執行，使用者可以選擇機器組；
• 它是一個訊息傳遞模型，
• 基於程序的計算；
• 支援異構體系結構。

資料並行程式設計

資料並行程式設計模型的主要重點是在資料集上同時執行操作。資料集被組織成一些結構，例如陣列、超立方體等。處理器對同一資料結構進行集體操作。每個任務都在同一資料結構的不同分割槽上執行。

它具有限制性，因為並非所有演算法都可以在資料並行性的術語中指定。這就是資料並行性並非普遍的原因。

資料並行語言有助於指定資料分解和對映到處理器。它還包括資料分佈語句，允許程式設計師控制資料 - 例如，哪些資料將在哪個處理器上 - 以減少處理器之間的通訊量。

並行演算法 - 結構

要正確應用任何演算法，選擇合適的資料結構非常重要。這是因為在特定資料結構上執行的特定操作可能需要更多時間，而與在另一個數據結構上執行相同的操作相比。

示例 - 使用陣列訪問集合中的第 i 個元素可能需要常數時間，但使用連結列表，執行相同操作所需的時間可能會變成多項式。

因此，必須考慮體系結構和要執行的操作型別來選擇資料結構。

以下資料結構在並行程式設計中常用：

• 連結列表
• 陣列
• 超立方體網路

連結列表

連結列表是一種資料結構，具有零個或多個透過指標連線的節點。節點可能佔用也可能不佔用連續的記憶體位置。每個節點都有兩個或三個部分 - 一個資料部分儲存資料，另外兩個是連結欄位，儲存前一個或下一個節點的地址。第一個節點的地址儲存在稱為頭部的外部指標中。最後一個節點，稱為尾部，通常不包含任何地址。

連結列表有三種類型：

• 單向連結列表
• 雙向連結列表
• 迴圈連結列表

單向連結列表

單向連結列表的節點包含資料和下一個節點的地址。一個稱為頭部的外部指標儲存第一個節點的地址。

雙向連結列表

雙向連結列表的節點包含資料以及前一個和下一個節點的地址。一個稱為頭部的外部指標儲存第一個節點的地址，一個稱為尾部的外部指標儲存最後一個節點的地址。

迴圈連結列表

迴圈連結列表與單向連結列表非常相似，只是最後一個節點儲存了第一個節點的地址。

陣列

陣列是一種資料結構，我們可以在其中儲存類似型別的資料。它可以是一維的或多維的。陣列可以是靜態建立的或動態建立的。

• 在靜態宣告的陣列中，陣列的維度和大小在編譯時已知。

• 在動態宣告的陣列中，陣列的維度和大小在執行時已知。

對於共享記憶體程式設計，陣列可以用作公共記憶體，對於資料並行程式設計，它們可以透過劃分為子陣列來使用。

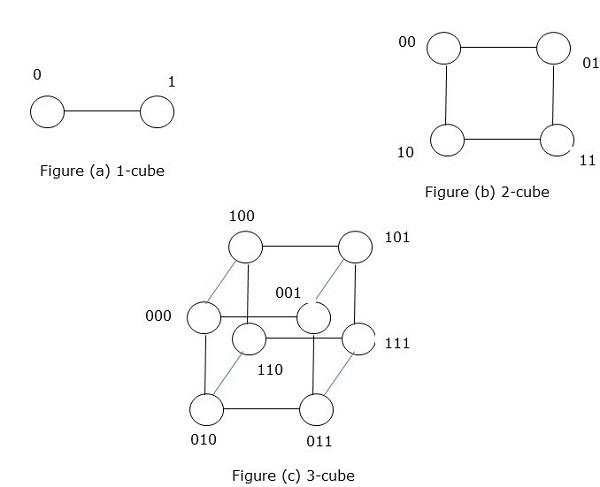
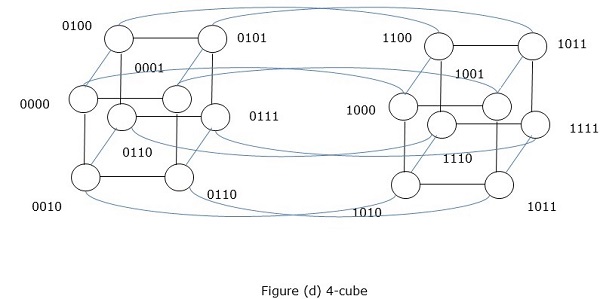
超立方體網路

超立方體體系結構對於那些每個任務都必須與其他任務通訊的並行演算法很有用。超立方體拓撲可以輕鬆嵌入其他拓撲，例如環和網格。它也稱為 n 維超立方體，其中n是維數。超立方體可以遞迴地構造。

並行演算法 - 設計技術

為並行演算法選擇合適的工程設計技術是最困難和最重要的任務。大多數並行程式設計問題可能有多個解決方案。在本章中，我們將討論以下並行演算法的工程設計技術：

• 分治法
• 貪心演算法
• 動態規劃
• 回溯法
• 分支限界法
• 線性規劃

分治法

在分治法中，問題被分解成幾個較小的子問題。然後遞迴地解決子問題，並將其組合以獲得原始問題的解決方案。

分治法在每個級別都涉及以下步驟：

• 分解 - 將原始問題分解成子問題。

• 解決 - 遞迴地解決子問題。

• 合併 - 將子問題的解決方案組合在一起，以獲得原始問題的解決方案。

分治法應用於以下演算法：

• 二分查詢
• 快速排序
• 歸併排序
• 整數乘法
• 矩陣求逆
• 矩陣乘法

貪心演算法

在貪心演算法最佳化解決方案中，在任何時刻都選擇最佳解決方案。貪心演算法非常易於應用於複雜問題。它決定下一步哪個步驟將提供最準確的解決方案。

此演算法稱為貪心，因為當提供較小例項的最優解時，演算法不會將整個程式作為一個整體考慮。一旦考慮了一個解決方案，貪心演算法就不會再考慮同一個解決方案。

貪心演算法遞迴地從最小的組成部分建立一組物件。遞迴是解決問題的一種過程，其中特定問題的解決方案取決於該問題較小例項的解決方案。

動態規劃

動態規劃是一種最佳化技術，它將問題分解成較小的子問題，並且在解決每個子問題後，動態規劃將所有解決方案組合在一起以獲得最終解決方案。與分治法不同，動態規劃多次重用子問題的解決方案。

斐波那契數列的遞迴演算法是動態規劃的一個例子。

回溯演算法

回溯是一種最佳化技術，用於解決組合問題。它適用於程式設計和現實生活問題。八皇后問題、數獨遊戲和穿過迷宮是使用回溯演算法的流行示例。

在回溯中，我們從一個可能的解決方案開始，該解決方案滿足所有必需的條件。然後我們進入下一級，如果該級沒有產生令人滿意的解決方案，我們返回一級並從一個新的選項開始。

分支限界法

分支限界演算法是一種最佳化技術，用於獲得問題的最優解。它在整個解空間中尋找給定問題的最佳解決方案。要最佳化的函式中的界限與最新最佳解決方案的值合併。它允許演算法完全找到解空間的一部分。

分支限界搜尋的目的是維護到目標的最低成本路徑。一旦找到解決方案，它就可以不斷改進解決方案。分支限界搜尋在深度有界搜尋和深度優先搜尋中實現。

線性規劃

線性規劃描述了一大類最佳化問題，其中最佳化準則和約束都是線性函式。它是一種獲得最佳結果的技術，例如最大利潤、最短路徑或最低成本。

在這種程式設計中，我們有一組變數，我們必須為它們分配絕對值以滿足一組線性方程，並最大化或最小化給定的線性目標函式。

並行演算法 - 矩陣乘法

矩陣是一組按固定行數和列數排列的數值和非數值資料。矩陣乘法是平行計算中一種重要的乘法設計。在這裡，我們將討論矩陣乘法在各種通訊網路（如網格和超立方體）上的實現。網格和超立方體具有更高的網路連線性，因此它們允許比其他網路（如環形網路）更快的演算法。

網格網路

一組節點形成一個p維網格的拓撲結構稱為網格拓撲結構。在這裡，所有邊都平行於網格軸，並且所有相鄰節點都可以相互通訊。

節點總數 =（行中節點數）×（列中節點數）

可以使用以下因素評估網格網路：

• 直徑
• 二分寬度

直徑 - 在網格網路中，兩個節點之間最長的距離是其直徑。具有kP個節點的p維網格網路的直徑為p(k–1)。

二分寬度 - 二分寬度是從網路中移除以將網格網路分成兩半所需的最小邊數。

使用網格網路的矩陣乘法

我們考慮了一個具有環繞連線的二維網格網路SIMD模型。我們將設計一種演算法，在特定時間內使用n²個處理器來乘以兩個n × n陣列。

矩陣A和B的元素分別為a_ij和b_ij。處理單元PE_ij表示a_ij和b_ij。以這樣一種方式排列矩陣A和B，使得每個處理器都有一對要乘以的元素。矩陣A的元素將向左移動，矩陣B的元素將向上移動。矩陣A和B中元素位置的這些變化為每個處理單元PE提供了一對新的要乘以的值。

演算法步驟

• 交錯兩個矩陣。
• 計算所有乘積，a_ik × b_kj
• 步驟2完成後計算總和。

演算法

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

超立方體網路

超立方體是一個n維結構，其中邊彼此垂直且長度相同。n維超立方體也稱為n-cube或n維立方體。

具有2^k個節點的超立方體的特徵

• 直徑 = k
• 二分寬度 = 2^k–1
• 邊數 = k

使用超立方體網路的矩陣乘法

超立方體網路的一般規範：

• 設N = 2^m為處理器總數。設處理器為P_0, P₁…..P_N-1。

• 設i和i^b為兩個整數，0 < i,i^b < N-1，並且它們的二進位制表示僅在位置b上不同，0 < b < k–1。

• 讓我們考慮兩個n × n矩陣，矩陣A和矩陣B。

• 步驟1 - 矩陣A和矩陣B的元素分配給n³個處理器，使得位置i，j，k處的處理器具有a_ji和b_ik。

• 步驟2 - 位置（i，j，k）中的所有處理器計算乘積

  C(i,j,k) = A(i,j,k) × B(i,j,k)

• 步驟3 - C(0,j,k) = ΣC(i,j,k)，其中0 ≤ i ≤ n-1，其中0 ≤ j, k < n–1。

分塊矩陣

分塊矩陣或分割槽矩陣是一個矩陣，其中每個元素本身表示一個單獨的矩陣。這些單獨的部分稱為塊或子矩陣。

示例

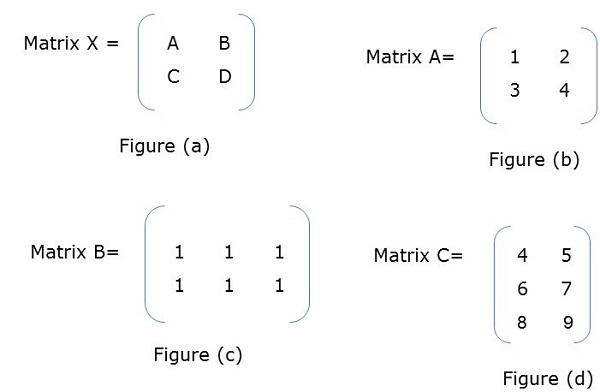
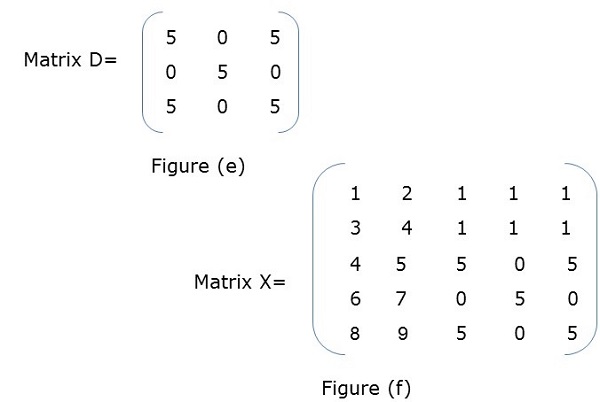
在圖（a）中，X是一個分塊矩陣，其中A、B、C、D本身是矩陣。圖（f）顯示了總矩陣。

分塊矩陣乘法

當兩個分塊矩陣是方陣時，它們的乘法方式與我們執行簡單矩陣乘法的方式相同。例如，

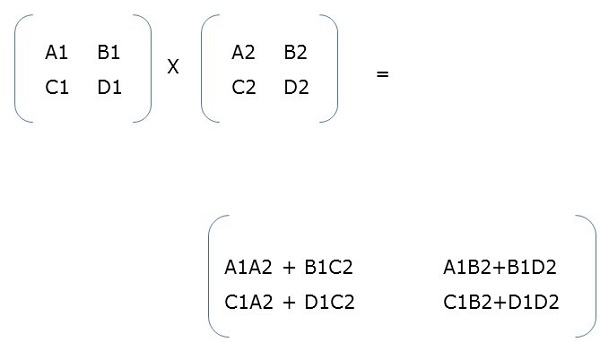
並行演算法 - 排序

排序是按特定順序（即升序、降序、字母順序等）排列一組元素的過程。這裡我們將討論以下內容：

• 列舉排序
• 奇偶交換排序
• 並行歸併排序
• 超快速排序

對元素列表進行排序是一種非常常見的操作。當我們需要對大量資料進行排序時，順序排序演算法可能效率不夠高。因此，排序中使用了並行演算法。

列舉排序

列舉排序是一種透過查詢每個元素在排序列表中的最終位置來排列列表中所有元素的方法。它是透過將每個元素與所有其他元素進行比較並查詢具有較小值的元素的數量來完成的。

因此，對於任意兩個元素a_i和a_j，以下情況之一必須為真：

• a_i < a_j
• a_i > a_j
• a_i = a_j

演算法

procedure ENUM_SORTING (n)

begin
   for each process P1,j do
      C[j] := 0;
		
   for each process Pi, j do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

奇偶交換排序

奇偶交換排序基於氣泡排序技術。它比較兩個相鄰的數字，如果第一個數字大於第二個數字，則交換它們，以獲得升序列表。相反的情況適用於降序序列。奇偶交換排序分為兩個階段：奇數階段和偶數階段。在這兩個階段中，程序與其右側的相鄰數字交換數字。

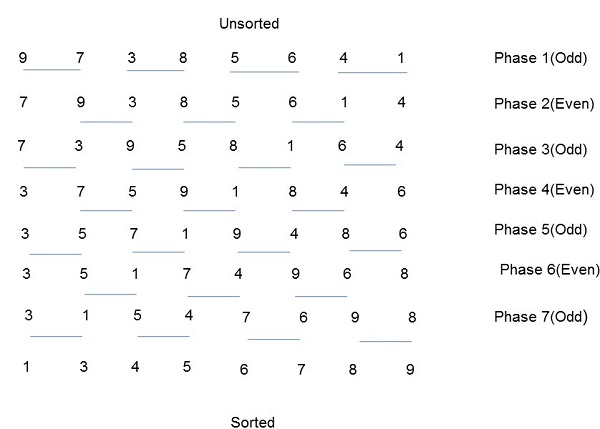
演算法

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

並行歸併排序

歸併排序首先將未排序的列表劃分為儘可能小的子列表，將其與相鄰列表進行比較，並按排序順序合併。它透過遵循分治演算法很好地實現了並行性。

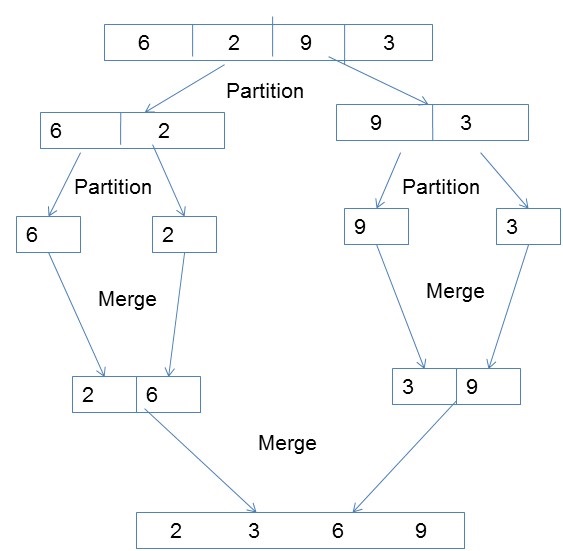
演算法

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

超快速排序

超快速排序是在超立方體上實現快速排序。其步驟如下：

• 將未排序的列表分配給每個節點。
• 在本地對每個節點進行排序。
• 從節點0廣播中值。
• 在本地拆分每個列表，然後透過最高維度交換一半。
• 並行重複步驟3和4，直到維度達到0。

演算法

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

並行搜尋演算法

搜尋是計算機科學中一項基本操作。它用於所有需要查詢元素是否在給定列表中的應用程式。在本章中，我們將討論以下搜尋演算法：

• 分治法
• 深度優先搜尋
• 廣度優先搜尋
• 最佳優先搜尋

分治法

在分治法中，問題被分解成幾個較小的子問題。然後遞迴地解決子問題，並將其組合以獲得原始問題的解決方案。

分治法在每個級別都涉及以下步驟：

• 分解 - 將原始問題分解成子問題。

• 解決 - 遞迴地解決子問題。

• 合併 - 將子問題的解決方案組合起來以獲得原始問題的解決方案。

二分查詢是分治演算法的一個例子。

虛擬碼

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

深度優先搜尋

深度優先搜尋（或DFS）是一種用於搜尋樹或無向圖資料結構的演算法。在這裡，概念是從稱為根的起始節點開始，並在同一分支中儘可能遠地遍歷。如果我們得到一個沒有後繼節點的節點，我們返回並繼續使用尚未訪問的頂點。

深度優先搜尋的步驟

• 考慮一個以前未訪問過的節點（根），並將其標記為已訪問。

• 訪問第一個相鄰的後繼節點並將其標記為已訪問。

• 如果所考慮節點的所有後繼節點都已訪問或它沒有更多後繼節點，則返回到其父節點。

虛擬碼

設v為圖G中搜索開始的頂點。

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

廣度優先搜尋

廣度優先搜尋（或BFS）是一種用於搜尋樹或無向圖資料結構的演算法。在這裡，我們從一個節點開始，然後訪問同一級別上的所有相鄰節點，然後移動到下一級別上的相鄰後繼節點。這也被稱為逐層搜尋。

廣度優先搜尋的步驟

• 從根節點開始，將其標記為已訪問。
• 由於根節點在同一級別上沒有節點，因此轉到下一級別。
• 訪問所有相鄰節點並將其標記為已訪問。
• 轉到下一級別並訪問所有未訪問的相鄰節點。
• 繼續此過程，直到所有節點都被訪問。

虛擬碼

設v為圖G中搜索開始的頂點。

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

最佳優先搜尋

最佳優先搜尋是一種遍歷圖以在最短路徑中到達目標的演算法。與BFS和DFS不同，最佳優先搜尋遵循一個評估函式來確定接下來遍歷哪個節點最合適。

最佳優先搜尋的步驟

• 從根節點開始，將其標記為已訪問。
• 找到下一個合適的節點並將其標記為已訪問。
• 轉到下一級別並找到合適的節點並將其標記為已訪問。
• 繼續此過程，直到到達目標。

虛擬碼

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

圖演算法

圖是一種用於表示物件對之間連線的抽象表示法。圖由以下部分組成：

• 頂點 - 圖中相互連線的物件稱為頂點。頂點也稱為節點。

• 邊 - 邊是連線頂點的連結。

圖有兩種型別：

• 有向圖 - 在有向圖中，邊具有方向，即邊從一個頂點到另一個頂點。

• 無向圖 - 在無向圖中，邊沒有方向。

圖著色

圖著色是一種為圖的頂點分配顏色，以便沒有兩個相鄰頂點具有相同顏色的方法。一些圖著色問題是：

• 頂點著色 - 為圖的頂點著色，以便沒有兩個相鄰頂點共享相同的顏色。

• 邊著色 - 它是一種為每條邊分配一種顏色，以便沒有兩條相鄰邊具有相同顏色的方法。

• 面著色 - 它為平面圖的每個面或區域分配一種顏色，以便沒有兩個共享公共邊界的面對具有相同的顏色。

色數

色數是為圖著色所需的最小顏色數。例如，以下圖的色數為3。

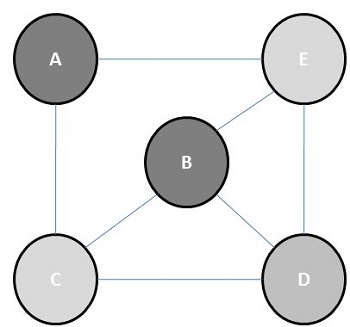
圖著色的概念應用於準備時間表、移動無線電頻率分配、數獨、暫存器分配和地圖著色。

圖著色的步驟

• 將n維陣列中每個處理器的初始值設定為1。

• 現在要為頂點分配特定顏色，請確定該顏色是否已分配給相鄰頂點。

• 如果處理器在相鄰頂點中檢測到相同顏色，則將其在陣列中的值設定為0。

• 進行n²次比較後，如果陣列的任何元素為1，則它是一個有效的著色。

圖著色的虛擬碼

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

最小生成樹

其所有邊的權重（或長度）之和小於圖G所有其他可能生成樹的生成樹稱為最小生成樹或最小成本生成樹。下圖顯示了一個加權連通圖。

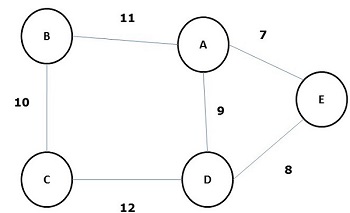
上面圖的一些可能的生成樹如下所示：

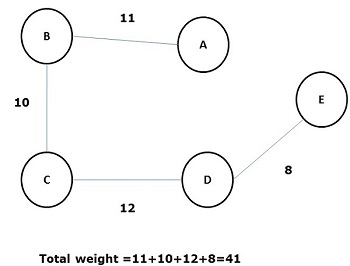
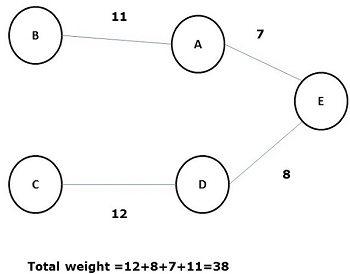
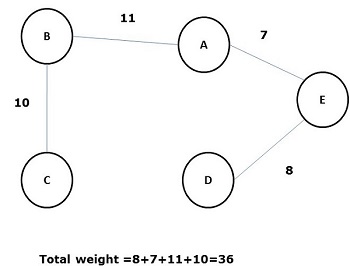
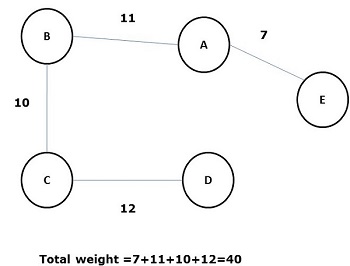
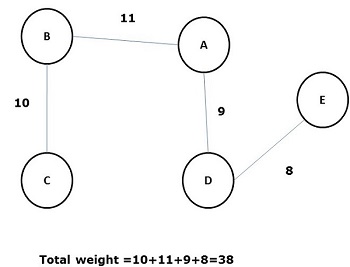
在所有上述生成樹中，圖（d）是最小生成樹。最小成本生成樹的概念應用於旅行商問題、電子電路設計、高效網路設計和高效路由演算法設計。

為了實現最小成本生成樹，使用了以下兩種方法：

• Prim演算法
• Kruskal演算法

Prim演算法

Prim演算法是一種貪心演算法，它可以幫助我們找到加權無向圖的最小生成樹。它首先選擇一個頂點，然後找到與該頂點關聯的具有最低權重的邊。

Prim演算法的步驟

• 選擇圖G的任何頂點，例如v₁。

• 選擇圖G的一條邊，例如e₁，使得e₁ = v₁ v₂，且v₁ ≠ v₂，並且e₁在圖G中與v₁關聯的邊中權重最小。

• 現在，根據步驟2，選擇與v₂關聯的權重最小的邊。

• 繼續此過程，直到選擇n-1條邊。這裡n是頂點的數量。

最小生成樹為：

克魯斯卡爾演算法

克魯斯卡爾演算法是一種貪心演算法，它幫助我們找到連通加權圖的最小生成樹，在每一步中新增成本遞增的弧。它是一種最小生成樹演算法，它找到連線森林中任何兩棵樹的權重儘可能小的邊。

克魯斯卡爾演算法的步驟

• 選擇權重最小的邊；例如圖G的e₁，並且e₁不是迴路。

• 選擇與e₁連線的下一條權重最小的邊。

• 繼續此過程，直到選擇n-1條邊。這裡n是頂點的數量。

上面圖的最小生成樹為：

最短路徑演算法

最短路徑演算法是一種找到從源節點(S)到目標節點(D)的最低成本路徑的方法。在這裡，我們將討論摩爾演算法，也稱為廣度優先搜尋演算法。

摩爾演算法

• 標記源頂點S，並將其標記為i，並設定i=0。

• 找到與標記為i的頂點相鄰的所有未標記頂點。如果沒有頂點與頂點S連線，則頂點D與S未連線。如果存在與S連線的頂點，則將其標記為i+1。

• 如果D已標記，則轉到步驟4，否則轉到步驟2以增加i=i+1。

• 找到最短路徑的長度後停止。