並行演算法 - 矩陣乘法

矩陣是由按固定行數和列數排列的數值和非數值資料組成的集合。矩陣乘法是平行計算中一種重要的乘法設計。在這裡，我們將討論在各種通訊網路（如網格和超立方體）上實現矩陣乘法的方案。網格和超立方體具有更高的網路連線性，因此它們允許比其他網路（如環形網路）更快的演算法。

網格網路

一組節點形成一個 p 維網格的拓撲結構稱為網格拓撲結構。在這裡，所有邊都平行於網格軸，並且所有相鄰節點都可以相互通訊。

節點總數 =（行中的節點數）×（列中的節點數）

可以使用以下因素評估網格網路：

直徑
二分寬度

直徑 - 在網格網路中，兩個節點之間最長的距離即為其直徑。具有kP個節點的 p 維網格網路的直徑為p(k–1)。

二分寬度 - 二分寬度是從網路中移除以將網格網路分成兩半所需的最小邊數。

使用網格網路進行矩陣乘法

我們考慮了一個具有環繞連線的二維網格網路 SIMD 模型。我們將設計一種演算法，使用 n² 個處理器在特定時間內乘以兩個 n × n 陣列。

矩陣 A 和 B 的元素分別為 a_ij 和 b_ij。處理單元 PE_ij 表示 a_ij 和 b_ij。以這樣的方式排列矩陣 A 和 B，使得每個處理器都有一對要相乘的元素。矩陣 A 的元素將向左移動，矩陣 B 的元素將向上移動。矩陣 A 和 B 中元素位置的這些變化為每個處理單元 PE 提供了一對新的要相乘的值。

演算法步驟

交錯兩個矩陣。
計算所有乘積，a_ik × b_kj
在步驟 2 完成後計算總和。

演算法

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

超立方體網路

超立方體是一個 n 維結構，其中邊彼此垂直且長度相同。n 維超立方體也稱為 n-cube 或 n 維立方體。

具有 2^k 個節點的超立方體的特徵

直徑 = k
二分寬度 = 2^k–1
邊數 = k

使用超立方體網路進行矩陣乘法

超立方體網路的一般規範：

令N = 2^m為處理器總數。令處理器為 P_0, P₁…..P_N-1。
令 i 和 i^b 為兩個整數，0 < i,i^b < N-1，並且它們的二進位制表示僅在位置 b 不同，0 < b < k–1。
讓我們考慮兩個 n × n 矩陣，矩陣 A 和矩陣 B。
步驟 1 - 矩陣 A 和矩陣 B 的元素被分配給 n³ 個處理器，使得位置 i、j、k 處的處理器具有 a_ji 和 b_ik。
步驟 2 - 位置 (i,j,k) 處的所有處理器都計算乘積

C(i,j,k) = A(i,j,k) × B(i,j,k)
步驟 3 - C(0,j,k) = ΣC(i,j,k)，其中 0 ≤ i ≤ n-1，其中 0 ≤ j, k < n–1。

分塊矩陣

分塊矩陣或分割槽矩陣是一個矩陣，其中每個元素本身代表一個單獨的矩陣。這些單獨的部分稱為塊或子矩陣。

示例

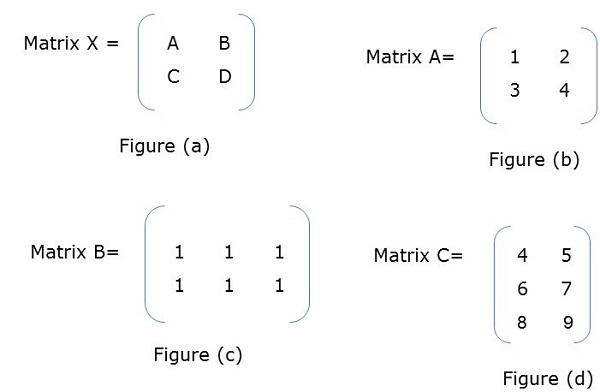
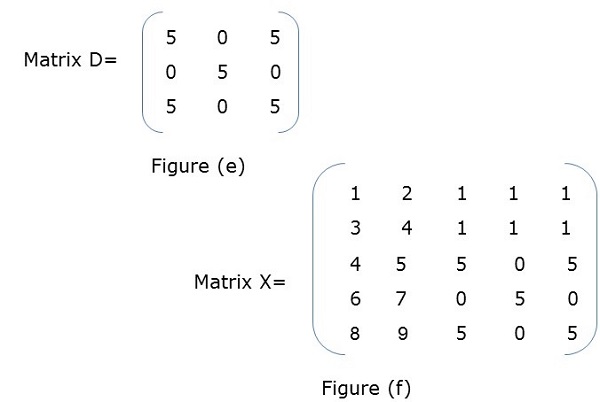
在圖 (a) 中，X 是一個分塊矩陣，其中 A、B、C、D 本身就是矩陣。圖 (f) 顯示了整個矩陣。

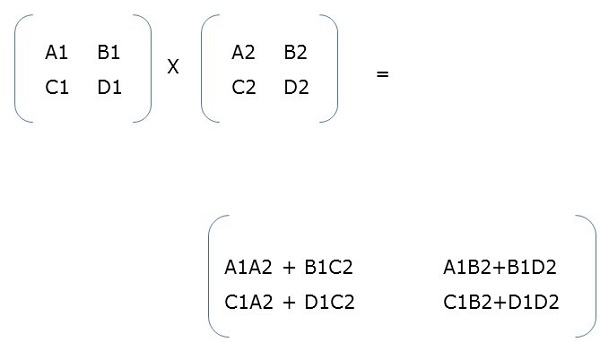
分塊矩陣乘法

當兩個分塊矩陣是方陣時，它們的乘法方式與我們執行簡單矩陣乘法的方式相同。例如，

列印頁面