圖演算法

---

---

圖是一種抽象的表示方法，用於表示物件對之間的連線。一個圖由：

• 頂點 - 圖中相互連線的物件稱為頂點。頂點也稱為節點。

• 邊 - 邊是連線頂點的連結。

圖有兩種型別：

• 有向圖 - 在有向圖中，邊具有方向，即邊從一個頂點指向另一個頂點。

• 無向圖 - 在無向圖中，邊沒有方向。

圖著色

圖著色是一種為圖的頂點分配顏色，使得任何兩個相鄰頂點不具有相同顏色的方法。一些圖著色問題包括：

• 頂點著色 - 一種為圖的頂點著色，使得任何兩個相鄰頂點不共享相同顏色的方法。

• 邊著色 - 這是一種為每條邊分配顏色，使得任何兩條相鄰邊不具有相同顏色的方法。

• 面著色 - 它為平面圖的每個面或區域分配一種顏色，使得任何兩個共享公共邊界的面對不具有相同顏色。

色數

色數是為圖著色所需的最少顏色數。例如，下圖的色數為 3。

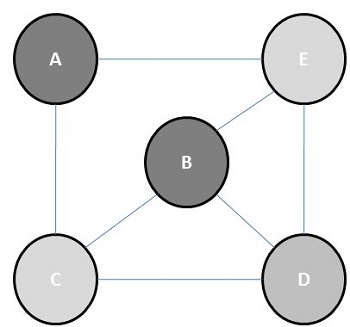
圖著色的概念應用於製作時間表、移動無線電頻率分配、數獨、暫存器分配和地圖著色。

圖著色步驟

• 將n維陣列中每個處理器的初始值設定為1。

• 現在，要為頂點分配特定顏色，請確定該顏色是否已分配給相鄰頂點。

• 如果處理器檢測到相鄰頂點具有相同顏色，則它將其在陣列中的值設定為0。

• 進行n²次比較後，如果陣列的任何元素為1，則這是一個有效的著色。

圖著色的虛擬碼

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

最小生成樹

其所有邊的權重（或長度）之和小於圖G所有其他可能生成樹的生成樹稱為最小生成樹或最小成本生成樹。下圖顯示了一個加權連通圖。

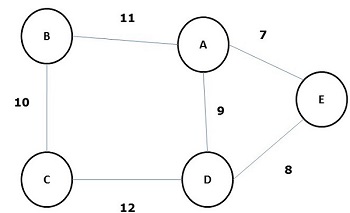
上圖的一些可能的生成樹如下所示：

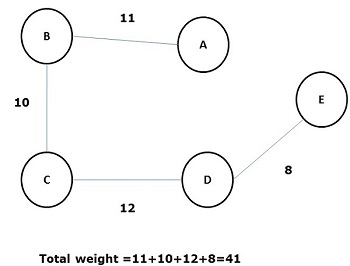
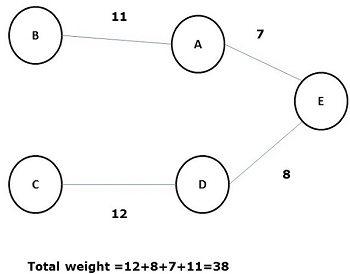
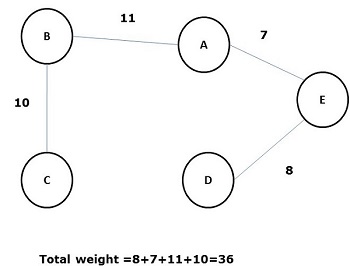
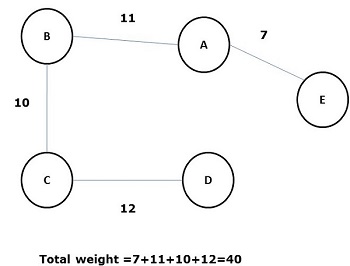
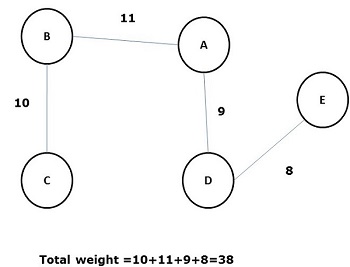
在所有上述生成樹中，圖(d)是最小生成樹。最小成本生成樹的概念應用於旅行商問題、電子電路設計、高效網路設計和高效路由演算法設計。

為了實現最小成本生成樹，使用以下兩種方法：

• Prim 演算法
• Kruskal 演算法

Prim 演算法

Prim 演算法是一種貪心演算法，它幫助我們找到加權無向圖的最小生成樹。它首先選擇一個頂點，然後找到與該頂點關聯的具有最低權重的邊。

Prim 演算法的步驟

• 選擇圖G的任何頂點，例如v₁。

• 選擇圖G的一條邊，例如e₁，使得e₁ = v₁v₂，且v₁ ≠ v₂，並且e₁在圖G中與v₁關聯的邊中具有最小權重。

• 現在，按照步驟2，選擇與v₂關聯的最小權重邊。

• 繼續此步驟，直到選擇了n-1條邊。這裡n是頂點數。

最小生成樹是：

Kruskal 演算法

Kruskal 演算法是一種貪心演算法，它幫助我們找到連通加權圖的最小生成樹，在每個步驟中新增成本遞增的弧。這是一種最小生成樹演算法，它找到連線森林中任何兩個樹的最小可能權重的邊。

Kruskal 演算法的步驟

• 選擇最小權重的邊；例如圖G中的e₁，且e₁不是環。

• 選擇連線到e₁的下一個最小權重的邊。

• 繼續此步驟，直到選擇了n-1條邊。這裡n是頂點數。

上圖的最小生成樹是：

最短路徑演算法

最短路徑演算法是一種查詢從源節點(S)到目標節點(D)的最低成本路徑的方法。在這裡，我們將討論 Moore 演算法，也稱為廣度優先搜尋演算法。

Moore 演算法

• 標記源頂點S，並將其標記為i，並設定i=0。

• 查詢與標記為i的頂點相鄰的所有未標記頂點。如果沒有任何頂點連線到頂點S，則頂點D未連線到S。如果有頂點連線到S，則將其標記為i+1。

• 如果D已標記，則轉到步驟4，否則轉到步驟2以增加i=i+1。

• 找到最短路徑的長度後停止。