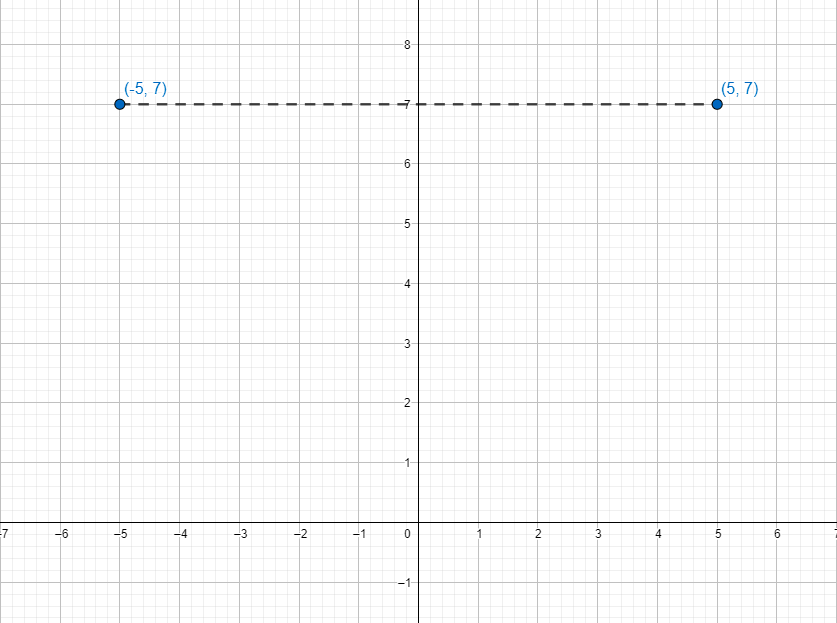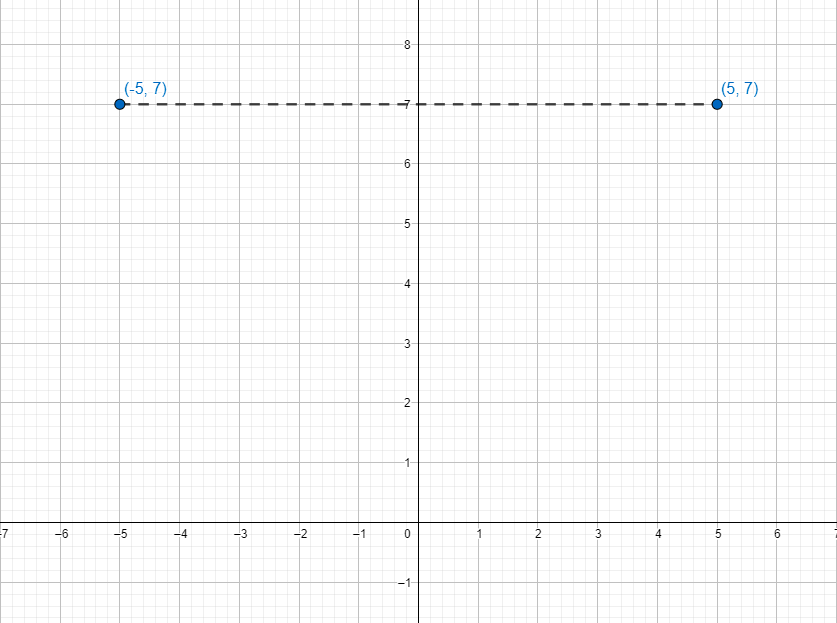點(-5, 7)關於y軸的對稱點的座標是
(a) (5, 7)
(b) (-5, -7)
(c) (5, -7)
(d) (7, -5)
已知：點(-5, 7)
求：點(-5, 7)關於y軸對稱點的座標。
解答:
這裡y軸充當平面鏡。
求點關於y軸對稱的規則
(i) 改變橫座標（即x座標）的符號。
(ii) 保留縱座標（即y座標）。
因此，所求點的座標是
(5, 7)
- 相關文章
- $( \frac{5}{7})^{-1}$的倒數是：$( i).\ \frac{5}{7}$$( ii).\ \frac{-5}{7}$$( iii).\ \frac{7}{5}$$( iv).\ \frac{-7}{5}$
- 化簡下列表達式：\( (5+\sqrt{7})(5-\sqrt{7}) \)
- 如果 $\frac{7+\sqrt{5}}{7-\sqrt{5}}=a+b \sqrt{5}$，求a和b。
- 下列哪些是隻包含數字的表示式？(a) \( y+3 \)(b) \( (7 \times 20)-8 z \)(c) \( 5(21-7)+7 \times 2 \)(d) 5(e) \( 3 x \)(f) \( 5-5 n \)(g) \( (7 \times 20)-(5 \times 10)-45+p \)
- 下列哪些是隻包含數字的表示式？(a) $y+3$(b) $(7\times 20)-8z$(c) $5(21-7)+7\times2$(d) 5(e) 3x(f) $5-5n$(g) $(7\times 20)-(5\times 10)-45+p$
- 化簡：\( \left(\frac{5^{-1} \times 7^{2}}{5^{2} \times 7^{-4}}\right)^{\frac{7}{2}} \times\left(\frac{5^{-2} \times 7^{3}}{5^{3} \times 7^{-5}}\right)^{\frac{-5}{2}} \)
- 證明點$A( 4,\ 2),\ B( 7,\ 5),\ C( 9,\ 7)$共線。
- 哪個更大？$( 5+7) \times 10$ 還是 $ 5+7\times10$？
- 化簡：\( \frac{7+3 \sqrt{5}}{3+\sqrt{5}}-\frac{7-3 \sqrt{5}}{3-\sqrt{5}} \)
- 求下列資料的眾數：3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4。
- 拋硬幣7次，正面朝上5次，則反面朝上的機率是(a.) \( \frac{2}{7} \)(b.) \( \frac{5}{7} \)(c.) \( \frac{1}{7} \)(d.) \( \frac{4}{7} \)
- 求和：$-5+\frac{7}{10}+\frac{3}{7}+(-3)+\frac{5}{14}+\frac{4}{5}$
- 將下列分數按升序排列。$\frac{4}{7}, \frac{7}{5}, \frac{2}{5}, \frac{5}{9}$。
- 求 $\frac{2}{7}\times\frac{5}{9}$ a) $\frac{2}{7}\times\frac{5}{9}$ 等於 $\frac{5}{9}\times\frac{2}{7}$ 嗎？ b) $\frac{2}{7}\times\frac{5}{9}$ 大於還是小於 $\frac{5}{9}\times\frac{2}{7}$？
- 用C++編寫求和程式：1 + (1+3) + (1+3+5) + (1+3+5+7) + ... + (1+3+5+7+....+(2n-1))
資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學