如果 A = {0, 1, 2, 3, 4, 5} 且 B = {2, 4, 6, 8, 10}，則求 A∪B 和 A∩B。並用文氏圖表示它們。

已知：

A = {0, 1, 2, 3, 4, 5}； B = {2, 4, 6, 8, 10}

求解

我們需要求 A∪B 和 A∩B，並用文氏圖表示它們。

解答

A = {0, 1, 2, 3, 4, 5}

B = {2, 4, 6, 8, 10}

A∪B 是 A 與 B 的並集 [將 A 和 B 中的元素合併，不重複]

A∪B = {0, 1, 2, 3, 4, 5, 6, 8, 10}

A∩B 是 A 與 B 的交集 [A 和 B 中共同的元素]

A∩B = {2, 4}

文氏圖

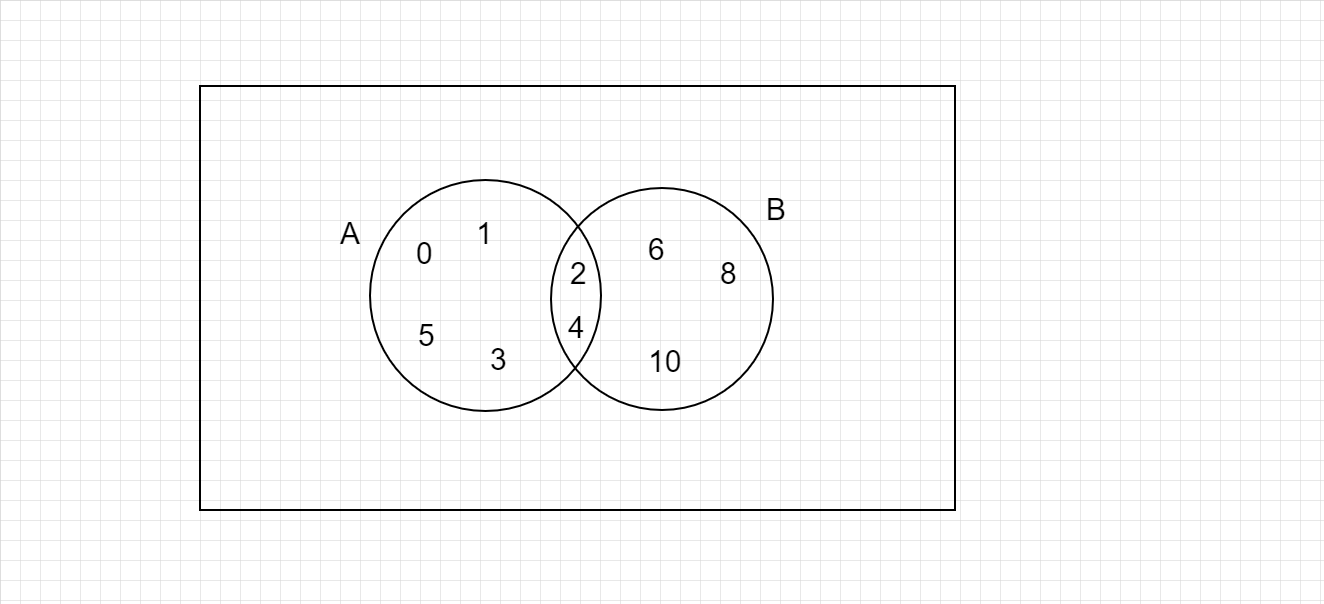
A∪B = {0, 1, 2, 3, 4, 5, 6, 8, 10}

A∩B = {2, 4}.

教程點

更新於：2022年10月10日

81 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習