資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學根據下列問題列出一對線性方程組，並用圖形法求解：5支鉛筆和7支鋼筆共計50盧比，而7支鉛筆和5支鋼筆共計46盧比。求一支鉛筆和一支鋼筆的價格。
已知
5支鉛筆和7支鋼筆共計50盧比，而7支鉛筆和5支鋼筆共計46盧比。 任務：
我們必須列出一對線性方程組並用圖形法求解。還要找出每支鉛筆和鋼筆的價格。
解答
設一支鉛筆和一支鋼筆的價格分別為x和y。
根據題意，
5x + 7y = 50 .....(i)
7x + 5y = 46 .....(ii)
為了用圖形表示上述方程，我們需要每個方程至少兩個解。
對於方程5x+7y=50，
7y=50-5x
y=(50-5x)/7
如果x=3，則y=(50-5*3)/7=(50-15)/7=35/7=5
如果x=10，則y=(50-5*10)/7=(50-50)/7=0/7=0
x | $3$ | $10$ |
y | $5$ | $0$ |
對於方程7x+5y=46，
5y=46-7x
y=(46-7x)/5
如果x=3，則y=(46-7*3)/5=(46-21)/5=25/5=5
如果x=8，則y=(46-7*8)/5=(46-56)/5=-10/5=-2
x | $3$ | $8$ |
| y | $7$ | $-2$ |
上述情況可以用下圖表示
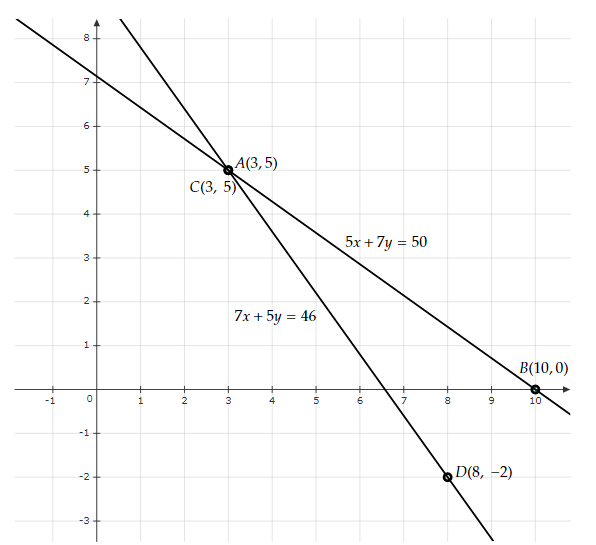
直線AB和CD分別表示方程5x+7y=50和7x+5y=46。
上述方程的解是它們的交點。
因此，
一支鉛筆的價格 x=3
一支鋼筆的價格 y=5
一支鉛筆和一支鋼筆的價格分別為3和5。
更新於：2022年10月10日
192 次瀏覽
廣告