資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究畫一個半徑為\( 4 \mathrm{~cm} \)的圓。畫出圓的任意兩條弦。作這兩條弦的垂直平分線。它們在哪裡相交？
待辦事項
我們必須構造給定弦的垂直平分線，並找到它們的交點。
解答
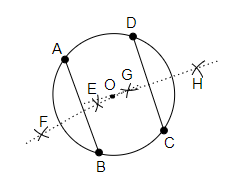
作圖步驟：
(i) 我們畫一個半徑為 $4\ cm$ 的圓，並將圓心命名為 $O$。
(ii) 現在，我們在圓上畫任意兩條弦，將第一條弦命名為 $\overline{AB}$，第二條弦命名為 $\overline{CD}$。
(iii) 現在，用圓規取大於 $\overline{AB}$ 長度一半的長度，從點 $A$ 和點 $B$ 分別在 $\overline{AB}$ 上方和下方畫兩條弧，並將弧的交點分別命名為 $E$ 和 $F$。
(iv) 同樣，用圓規取大於 $\overline{CD}$ 長度一半的長度，從點 $C$ 和點 $D$ 分別在 $\overline{CD}$ 上方和下方畫兩條弧，並將弧的交點分別命名為 $G$ 和 $H$。
(v) 現在，我們連線點 $E$ 和 $F$，以及點 $G$ 和 $H$。
(vi) 因此，$\overline{EF}$ 和 $\overline{GH}$ 分別構成 $\overline{AB}$ 和 $\overline{CD}$ 的垂直平分線，當兩條平分線都延長時，我們可以觀察到它們相交於圓心 $O$。
更新於： 2022年10月10日
48 次瀏覽
廣告