一個物體放置在凸面鏡前40釐米處，該凸面鏡的曲率半徑為40釐米。列出形成的像的四個特性。

已知：一個物體放置在凸面鏡前40釐米處，該凸面鏡的曲率半徑為40釐米

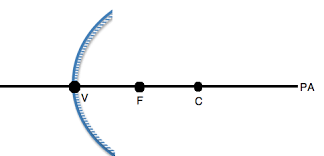
因此，$u = - 40 \ cm, \ R = + 40 \ cm$

焦距 $f = \frac{R}{2} = \frac{40}{2}$

使用鏡面公式

$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$

我們可以改寫為：$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

因此，$\frac{1}{v}=\frac{1}{20}-\frac{1}{-40}=\frac{3}{40}$

因此，$v=\frac{40}{3} \mathrm{cm}$

我們也知道放大率，$m = \frac{-v}{u}$

$m = \frac{-\frac{40}{3}}{- 40}$

因此，$m = \frac{1}{3}$

根據 $v$ 和 $m$ 的值，我們可以確定影像的以下特徵

• 由於 $v$ 為正，因此像是虛像
• 由於 $m$ 為正，因此像是正立的
• 由於 $m$<1，因此像是縮小的
• 由於 $0 < m < 1$，因此像是位於焦點和鏡面極點之間

教程點

更新於：2022年10月10日

1K+ 次瀏覽

啟動您的職業生涯

完成課程後獲得認證

開始