資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究自耦變壓器的輸出和變壓器銅材的節省
自耦變壓器的執行原理
理想降壓自耦變壓器的連線圖如圖所示。其中繞組ab是初級繞組，有N1匝；繞組bc是次級繞組，有N2匝。這裡，I1是輸入初級電流，I2是輸出次級電流或負載電流。
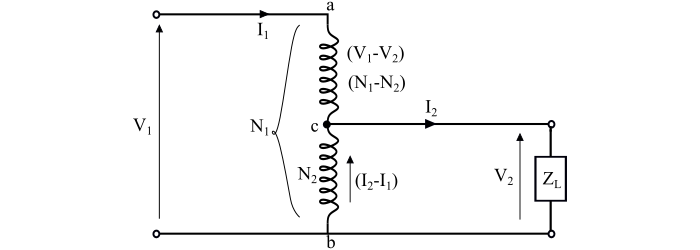
現在，繞組'ac'部分的匝數為N1 – N2匝，該部分的電壓為V1 – V2。公共部分（繞組'bc'）中的電流為I2 – I1。
考慮如圖所示的自耦變壓器的等效電路。從這個等效電路中，我們得到：
$$\mathrm{\frac{𝑉_{2}}{𝑉_{1}\:−\:𝑉_{2}}=\frac{𝑁_{2}}{𝑁_{1}\:−\:𝑁_{2}}}$$
$$\mathrm{\Rightarrow\:𝑁_{1}𝑉_{2}\:−\:𝑁_{2}𝑉_{2} = 𝑁_{2}𝑉_{1}\:−\:𝑁_{2}𝑉_{2}}$$
$$\mathrm{\Rightarrow\:𝑁_{1}𝑉_{2} = 𝑁_{2}𝑉_{1}}$$
$$\mathrm{\Rightarrow\:\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝑁_{2}}{𝑁_{1}}= 𝑎_{𝐴}… (1)}$$
公式(1)稱為自耦變壓器的電壓變換比。
此外，從自耦變壓器的等效電路中，我們有：
$$\mathrm{(𝑉_{1}\:−\:𝑉_{2})𝐼_{1}= 𝑉_{2}(𝐼_{2}\:−\:𝐼_{1})}$$
$$\mathrm{\Rightarrow\:𝑉_{1}𝐼_{1}\:−\:𝑉_{2}𝐼_{1} = 𝑉_{2}𝐼_{2}\:−\:𝑉_{2}𝐼_{1}}$$
$$\mathrm{\Rightarrow\:𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}}$$
$$\mathrm{\Rightarrow\:\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝐼_{1}}{𝐼_{2}}… (2)}$$
從公式(1)和(2)，我們得到：
$$\mathrm{\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝑁_{2}}{𝑁_{1}}=\frac{𝐼_{1}}{𝐼_{2}}= 𝑎_{𝐴}… (3)}$$
由於給定的自耦變壓器是理想的，因此：
$$\mathrm{𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}… (4)}$$
$$\mathrm{\Rightarrow\: 輸入視在功率 = 輸出視在功率}$$
自耦變壓器的輸出
由於自耦變壓器的初級和次級繞組既有磁連線也有電連線。因此，功率從初級側傳遞到次級側既有磁性（感應）方式，也有傳導方式。
這裡：
$$\mathrm{輸出視在功率 = 𝑉_{2}𝐼_{2}}$$
$$\mathrm{感應傳遞功率\:= \:𝑉_{2}(𝐼_{2}\:−\:𝐼_{1})}$$
$$\mathrm{∵\:𝐼_{1}\:=\:𝑎_{𝐴}𝐼_{2}}$$
$$\mathrm{∴\:感應傳遞功率 = 𝑉_{2}(𝐼_{2}\:−\:𝑎_{𝐴}𝐼_{2}) = 𝑉_{2}𝐼_{2}(1\:−\:𝑎_{𝐴})}$$
由於：
$$\mathrm{𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}}$$
因此：
$$\mathrm{感應傳遞功率 \:=\:𝑉_{1}𝐼_{1}(1\:−\:𝑎_{𝐴}) = 輸入功率 × (1\:− \:𝑎_{𝐴}) … (5)}$$
公式(5)給出了從初級到次級磁性傳遞的功率量。
現在，傳導傳遞的功率由下式給出：
$$\mathrm{傳導傳遞功率\:=\\: (輸入功率)\:−\:(感應傳遞功率)}$$
$$\mathrm{\Rightarrow\:傳導傳遞功率 = (輸入功率)\:−\:[輸入功率\:×\:(1\:−\:𝑎_{𝐴})]}$$
$$\mathrm{= 輸入功率\:×\:(1\:−\:(1\:−\:𝑎_{𝐴}))}$$
$$\mathrm{傳導傳遞功率 = 輸入功率\:×\:𝑎_{𝐴}… (6)}$$
公式(6)給出了從初級到次級電傳導的功率量。
變壓器導體材料（銅）的節省
對於相同的額定值，即相同的輸出和相同的變比，與普通的雙繞組變壓器相比，自耦變壓器需要的導體材料（銅）更少。該圖顯示了一個雙繞組變壓器（左）和一個自耦變壓器（右），兩者額定值相同。
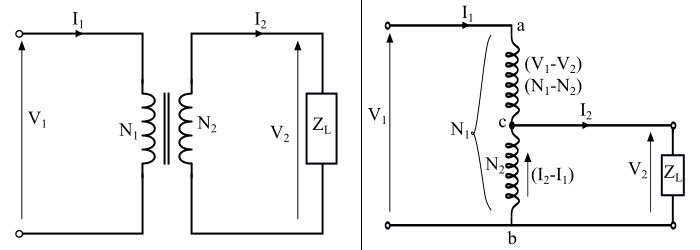
繞組中所需的銅線長度與繞組的匝數成正比，導線的橫截面積與電流額定值成正比。因此，繞組中所需的銅材料的體積和重量與電流和繞組匝數的乘積成正比，即：
$$\mathrm{所需銅材重量 \:∝\:電流 × 匝數}$$
對於雙繞組變壓器：
$$\mathrm{所需銅材重量\:∝ \:(𝐼_{1}𝑁_{1}+ 𝐼_{2}𝑁_{2})}$$
對於自耦變壓器：
$$\mathrm{ac段所需銅材重量\:∝\:𝐼_{1}(𝑁_{1} − 𝑁_{2})}$$
$$\mathrm{bc段所需銅材重量\:∝\:(𝐼_{2} − 𝐼_{1})𝑁_{2}}$$
因此：
$$\mathrm{所需銅材總重量 \:∝ [𝐼_{1}(𝑁_{1} − 𝑁_{2}) + (𝐼_{2} − 𝐼_{1})𝑁_{2}]}$$
現在，比較自耦變壓器和雙繞組變壓器所需的銅材重量，我們得到：
$$\mathrm{\frac{自耦變壓器所需銅材重量\:(𝑊_{𝑎})}{雙繞組變壓器所需銅材重量\:(𝑊𝑜)}\=\frac{[𝐼_{1}(𝑁_{1} − 𝑁_{2}) + (𝐼_{2} − 𝐼_{1})𝑁_{2}]}{(𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2})}}$$
$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=\frac{𝐼_{1}𝑁_{1} − 𝐼_{1}𝑁_{2} + 𝐼_{2}𝑁_{2} − 𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}=\frac{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2} − 2𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}}$$
$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=1-\frac{2𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}}$$
$$\mathrm{∵\:𝐼_{2}𝑁_{2}= 𝐼_{1}𝑁_{1}}$$
$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=1-\frac{2𝐼_{1}𝑁_{2}}{2𝐼_{1}𝑁_{1}}=1-\frac{𝑁_{2}}{𝑁_{1}}= (1 − 𝑎_{𝐴})}$$
因此，自耦變壓器所需的銅材重量為
$$\mathrm{(自耦變壓器所需銅材重量\:(𝑊_{𝑎})) =\ (1 − 𝑎_{𝐴}) ×(雙繞組變壓器所需銅材重量\:(𝑊_{𝑜})) … (7)}$$
因此，與雙繞組變壓器相比，自耦變壓器中銅材的節省量由下式給出：
$$\mathrm{銅材節省量 = 𝑊_{𝑜 }− 𝑊_{𝑎} = 𝑊_{𝑜} − (1 − 𝑎_{𝐴})𝑊_{𝑜}}$$
$$\mathrm{\Rightarrow\:銅材節省量 = 𝑎_{𝐴} × 𝑊_{𝑜} … (8)}$$
公式(8)給出了自耦變壓器中銅材節省量的值。很明顯，自耦變壓器的𝑎𝐴值越接近1，銅材的節省量就越大。
瀏覽量：3000+
