資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究變壓器的電動勢方程 – 變壓器的匝數比和變比
變壓器的電動勢方程
假設一個交流電壓施加到變壓器初級繞組上，電源電壓的頻率為f。此施加的電壓在變壓器鐵芯中產生正弦磁通φ，表示為：
$$\mathrm{\varphi = \varphi_{𝑚} sin \omega t}$$
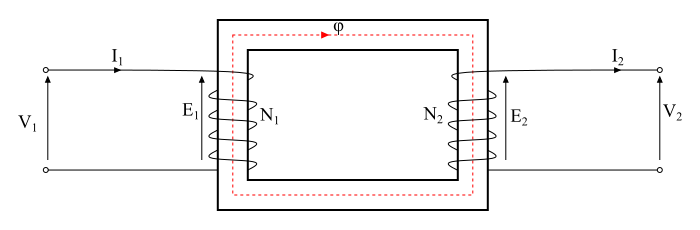
由於此正弦磁通，在初級繞組中感應出電動勢，其瞬時值由下式給出：
$$\mathrm{𝑒_{1} = −𝑁_{1}\frac{𝑑\varphi}{𝑑𝑡} = −𝑁_{1}\frac{𝑑}{𝑑𝑡}(\varphi_{𝑚} sin \omega t)}$$
$$\mathrm{⇒ 𝑒_{1} = −𝑁_{1}\omega\varphi_{𝑚} cos \omega t = 𝑁_{1}\omega\varphi_{𝑚} sin (\omega t −\frac{\pi}{2})}$$
$$\mathrm{\because \: \omega = 2\pi𝑓}$$
$$\mathrm{\therefore 𝑒_{1} = 2𝜋𝑓𝑁_{1}\varphi_{𝑚} sin (\omega t −\frac{\pi}{2})}$$
$$\mathrm{⇒ 𝑒_{1} = 𝐸_{𝑚1} sin (\omega t −\frac{\pi}{2})}$$
其中，Em1 是初級繞組中感應電動勢的最大值。
從這個表示式可以清楚地看出，初級繞組中的感應電動勢 (E1) 落後於磁通 90°。
$$\mathrm{𝐸_{𝑚1} = 𝑁_{1}𝜔\varphi_{𝑚} = 2𝜋𝑓𝑁_{1}\varphi_{𝑚}}$$
現在，對於正弦波，初級電動勢 (E1) 的 RMS 值由下式給出：
$$\mathrm{𝐸_{1} =\frac{𝐸_{𝑚1}}{\sqrt{2}}=\frac{2𝜋𝑓𝑁_{1}\varphi_{𝑚}}{\sqrt{2}}}$$
$$\mathrm{⇒ 𝐸_{1} = 4.44 𝑓\varphi_{𝑚}𝑁_{1} … (1)}$$
類似地，次級電動勢 (E2) 的 RMS 值由下式給出：
$$\mathrm{𝐸_{2} = 4.44 𝑓\varphi_{𝑚}𝑁_{2} … (2)}$$
公式 (1) 和 (2) 中的表示式稱為變壓器的電動勢方程。
因此，一般來說，變壓器的電動勢方程表示為：
$$\mathrm{𝐸 = 4.44 𝑓\varphi_{𝑚}𝑁 … (3)}$$
現在，取公式 (1) 和 (2) 的比率，我們得到：
$$\mathrm{\frac{𝐸_{1}}{𝐸_{2}}=\frac{𝑁_{1}}{𝑁_{2}}}$$
$$\mathrm{⇒ \frac{𝐸_{1}}{𝑁_{1}}=\frac{E_{2}}{𝑁_{2}}… (4)}$$
從公式 (4) 可以清楚地看出，初級繞組和次級繞組中每匝感應電動勢相同。
變壓器的匝數比
變壓器的匝數比定義為初級繞組匝數與次級繞組匝數之比，即
$$\mathrm{匝數比 =\frac{初級繞組匝數 (𝑁_{1})}{次級繞組匝數 (𝑁_{2})}}$$
因此，從公式 (1) 和 (2)，我們有：
$$\mathrm{⇒ 匝數比 =\frac{𝑁_{1}}{𝑁_{2}}=\frac{𝐸_{1}}{𝐸_{2}}}$$
對於理想變壓器，E1 = V1 和 E2 = V2，因此，
$$\mathrm{匝數比 =\frac{𝑁_{1}}{𝑁_{2}}=\frac{𝐸_{1}}{𝐸_{2}}=\frac{𝑉_{1}}{V_{2}}}$$
此外，對於理想變壓器，輸入伏安等於輸出伏安，即
$$\mathrm{𝑉_{1}𝐼_{1} = V_{2}I_{2}}$$
$$\mathrm{⇒\frac{𝑉_{1}}{V_{2}}=\frac{I_{2}}{𝐼_{1}}}$$
因此，
$$\mathrm{匝數比 =\frac{𝑁_{1}}{𝑁_{2}}=\frac{𝐸_{1}}{𝐸_{2}}=\frac{𝑉_{1}}{V_{2}}=\frac{I_{2}}{𝐼_{1}}\:… (5)}$$
變壓器的變比
變壓器的變比定義為變壓器輸出電壓與輸入電壓之比，即
$$\mathrm{變比，𝐾 =\frac{輸出電壓 (V_{2})}{輸入電壓 (𝑉_{1})}}$$
此外，從公式 (1) 和 (2)，我們得到
$$\mathrm{\frac{𝐸_{2}}{𝐸_{1}}=\frac{𝑁_{2}}{𝑁_{1}}}$$
對於理想變壓器，
$$\mathrm{\frac{V_{2}}{𝑉_{1}}=\frac{𝐸_{2}}{𝐸_{1}}}$$
以及
$$\mathrm{𝑉_{1}𝐼_{1} = V_{2}I_{2}}$$
$$\mathrm{⇒\frac{V_{2}}{𝑉_{1}}=\frac{𝐼_{1}}{I_{2}}}$$
因此，變壓器的變比由下式給出：
$$\mathrm{𝐾 =\frac{V_{2}}{𝑉_{1}}=\frac{𝐸_{2}}{𝐸_{1}}=\frac{𝑁_{2}}{𝑁_{1}}=\frac{𝐼_{1}}{I_{2}}\:… (6)}$$
從公式 (5) 和 (6)，可以看出，
$$\mathrm{匝數比 =\frac{1}{變比 (𝐾)}}$$
5K+ 次檢視
