多路複用器設計流程及應用

---

多路複用器（MUX）是一種數字組合邏輯電路，它接收多個數據輸入，並允許一次只傳輸其中一個到輸出通道。多路複用器由 2ⁿ 個輸入線、n 個選擇線和一個輸出線組成。在多路複用器中，所需資料輸入到輸出通道的路由由施加到選擇線的邏輯電平確定。多路複用器的功能框圖如圖 1 所示。

本文主要目的是解釋不同型別多路複用器電路的設計流程。更具體地說，我們將討論以下三種類型多路複用器的設計流程：

• 2:1 多路複用器
• 4:1 多路複用器
• 8:1 多路複用器

所以，讓我們現在討論這三種類型多路複用器各自的設計。

設計 2:1 多路複用器

2:1 多路複用器 (MUX) 具有 2 個輸入線 (I₀ 和 I₁)、1 個選擇線 (S) 和 1 個輸出線 (Y)。施加到選擇線 S 的邏輯電平決定哪個資料輸入將透過輸出線。

為了確定 2:1 多路複用器的輸出 (Y) 的布林表示式及其邏輯電路實現，我們首先需要它的功能表（真值表），該表提供有關電路操作的資訊。資料輸入為 I0 和 I1 的 2:1 多路複用器的功能表如下所示。

選擇線 (S)	輸出 (Y)
0	I0
1	I1

利用此真值表，我們可以寫出 2:1 MUX 輸出的邏輯表示式為：

$$Y=\bar{S}I_{0}+SI_{1}$$

要實現此邏輯表示式，我們需要兩個與門、一個非門和一個或門。2:1 MUX 的邏輯電路如圖 2 所示。

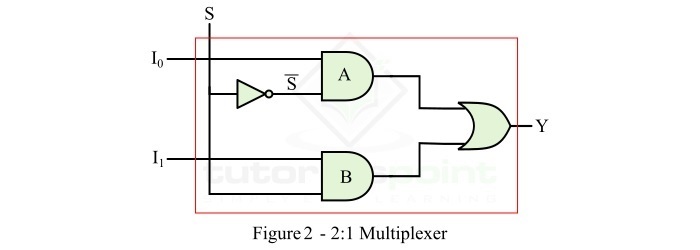
操作

圖 2 中所示的 2:1 MUX 的邏輯電路的工作原理如下：

• 當 S = 0 時，與門 A 被使能，與門 B 被停用。因此，輸出 Y = I₀。

• 當 S = 1 時，與門 A 被停用，與門 B 被使能。因此，輸出 Y = I₁。

這就是我們如何設計 2:1 多路複用器。

設計 4:1 多路複用器

4:1 多路複用器 (MUX) 是一種具有 4 個輸入線 (I₀、I₁、I₂ 和 I₃)、2 個選擇線 (S₀ 和 S₁) 和 1 個輸出線 (Y) 的 MUX。施加到選擇線 S₀ 和 S₁ 的邏輯電平決定哪個資料輸入將傳輸到輸出線。

為了確定 4:1 多路複用器的輸出 (Y) 的布林表示式及其邏輯電路，我們需要它的功能表（真值表），該表提供有關其電路操作的資訊。資料輸入為 I₀、I₁、I₂ 和 I₃ 的 4:1 多路複用器的功能表如下所示。

選擇線		輸出(Y)
S1	S0
0	0	I0
0	0	I1
1	0	I2
1	1	I3

利用此真值表，我們可以寫出 4:1 MUX 輸出的邏輯表示式為：

$$Y=\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{1}}S_{0}I_{1}+S_{1}\bar{S_{0}}I_{2}+S_{1}S_{0}I_{3}$$

要實現此邏輯表示式，我們需要四個與門、兩個非門和一個或門。因此，4:1 MUX 的邏輯電路如圖 3 所示。

操作

圖 3 中所示的 4:1 MUX 的邏輯電路的工作原理如下：

• 當 S₁ = 0 且 S₀ = 0 時，與門 A 被使能，與門 B、C 和 D 被停用。因此，輸出 Y = I₀。

• 當 S₁ = 0 且 S₀ = 1 時，與門 B 被使能，與門 A、C 和 D 被停用。因此，輸出 Y = I₁。

• 當 S₁ = 1 且 S₀ = 0 時，與門 C 被使能，與門 A、B 和 D 被停用。因此，輸出 Y = I₂。

• 當 S₁ = 1 且 S₀ = 1 時，與門 D 被使能，與門 A、B 和 C 被停用。因此，輸出 Y = I₃。

這樣，我們就可以設計一個 4:1 多路複用器。

設計 8:1 多路複用器

8:1 多路複用器 (MUX) 是一種組合邏輯電路，它具有 8 個輸入線 (I₀、I₁、I₂、I₃、I₄、I₅、I₆ 和 I₇)、3 個選擇線 (S₀、S₁ 和 S₂) 和 1 個輸出線 (Y)。施加到選擇線 S₀、S₁ 和 S₂ 的邏輯電平決定哪個資料輸入將傳輸到輸出線。

為了確定 8:1 多路複用器的輸出 (Y) 的邏輯表示式及其邏輯電路，我們需要它的功能表（真值表），該表提供有關其邏輯電路操作的資訊。

資料輸入為 I₀、I₁、I₂、I₃、I₄、I₅、I₆ 和 I₇，選擇線為 S₀、S₁ 和 S₂ 的 8:1 多路複用器的功能表如下所示。

選擇線			輸出 (Y)
S2	S1	S0
0	0	0	I0
0	0	1	I1
0	1	0	I2
0	1	1	I3
1	0	0	I4
1	0	1	I5
1	1	0	I6
1	1	1	I7

利用此功能表，我們可以寫出 8:1 MUX 輸出的邏輯表示式為：

$$Y=\bar{S_{2}}\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{2}}\bar{S_{1}}S_{0}I_{1}+\bar{S_{2}}S_{1}\bar{S_{0}}I_{2}+\bar{S_{2}}S_{1}S_{0}I_{3}+S_{2}\bar{S_{1}}\bar{S_{0}}I_{4}+S_{2}\bar{S_{1}}S_{0}I_{5}+S_{2}S_{1}\bar{S_{0}}I_{6}+S_{2}S_{1}S_{0}I_{7}$$

要實現此邏輯表示式，我們需要八個與門、三個非門和一個或門。因此，8:1 MUX 的邏輯電路如圖 4 所示。

操作

圖 4 中所示的 8:1 MUX 的邏輯電路的工作原理如下：

• 當 S₂ = 0、S₁ = 0 和 S₀ = 0 時，與門 A 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₀。

• 當 S₂ = 0、S₁ = 0 和 S₀ = 1 時，與門 B 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₁。

• 當 S₂ = 0、S₁ = 1 和 S₀ = 0 時，與門 C 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₂。

• 當 S₂ = 0、S₁ = 1 和 S₀ = 1 時，與門 D 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₃。

• 當 S₂ = 1、S₁ = 0 和 S₀ = 0 時，與門 E 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₄。

• 當 S₂ = 1、S₁ = 0 和 S₀ = 1 時，與門 F 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₅。

• 當 S₂ = 1、S₁ = 1 和 S₀ = 0 時，與門 G 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₆。

• 當 S₂ = 1、S₁ = 1 和 S₀ = 1 時，與門 H 被使能，邏輯電路中的所有其他與門都被停用。因此，輸出 Y = I₇。

這樣，我們就可以設計一個 8:1 多路複用器。

多路複用器的應用

多路複用器是數字系統中廣泛使用的組合邏輯電路之一。多路複用器的一些重要應用如下所示。

• 多路複用器用作資料選擇器。

• 多路複用器用於通訊系統以提高系統效率。

• 多路複用器用於電話網路，將多個音訊訊號整合到一條傳輸線上。

• 為了維護大量資料，多路複用器也用於計算機儲存系統。

• 多路複用器也用於電視廣播系統。

• 多路複用器用於衛星通訊和 GPS（全球定位系統）。

• 多路複用器也用於 PLC（可程式設計邏輯控制器）系統等。

這就是多路複用器設計流程和多路複用器的應用的全部內容。