資料的中位數

---

簡介

任何一個群體的中位數都是落在中間的那個值。在這個位置，一半的資料大於它，一半的資料小於它。中位數使我們能夠用一個值來表示大量的資料點。中位數是最容易計算的統計量。為了計算中位數，首先將資料按升序排列，然後中間的資料點就是資料的中位數。

集中趨勢

中位數是三種集中趨勢度量之一。在討論一組資料時，我們會關注資料集中間的位置。這被稱為集中趨勢度量。最常用的三種集中趨勢度量是平均數、中位數和眾數。

在本教程中，我們將只關注中位數。

中位數

中位數是指一組資料中的中間數字或中心值。它也是落在範圍中間的數字。

為了求出中位數，首先需要將資料從最小值到最大值或從最大值到最小值排序。中位數是介於總體、機率分佈或資料樣本的上半部分和下半部分之間的值。對於不同型別的分佈，中位數是不同的。

讓我們看一個例子，瞭解如何求出一組給定資料的中間值。

步驟 1 - 考慮數字 5、5、7、4 和 3。讓我們按升序排列這些數字：3、4、5、5、7。

步驟 2 - 統計這些值。

共有 5 個值。

步驟 3 - 找到中間值。

中間值就是中位數。因此，中位數是 5。

未分組資料中位數（奇數個條目）

以下步驟在使用未分組資料的中位數公式時很有幫助。

步驟 1 - 將資訊按升序或降序排列。

步驟 2 - 接下來，統計觀察值的總數 'n'。

步驟 3 - 確定 'n' 是偶數個觀察值還是奇數個觀察值。

如果資料有奇數個條目，則對於一組給定的數字（例如，具有 "n" 個奇數觀察值的數字），公式可以寫成如下形式：

$$\mathrm{Median=[\frac{(n+1)}{2}]^{th} term}$$

未分組資料中位數（偶數個條目）

對於一組給定的數字（例如，具有 "n" 個偶數觀察值的數字），中位數公式可以寫成如下形式：

$$\mathrm{Median= \frac{[(\frac{n}{2})^{th} term+((\frac{n}{2})+1)^{th} term]}{2}}$$

分組資料的中位數

當資料是連續的並表示為頻率分佈時，使用以下步驟來確定中位數。

步驟 1 - 第一步是找到觀察值的總數 (n)。

步驟 2 - 確定組距 (h) 併為資料建立不同的組。

步驟 3 - 第三步是計算每個組的累積頻率。

步驟 4 - 確定中位數屬於哪個組。（N/2 位於由中位數定義的組中。）

步驟 5 - 確定中位陣列（下限）的限值和中位陣列之前的組的累積頻率 (c)。

現在可以使用以下公式確定中位數的值。

$$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$$

小於累積頻率表

要製作小於累積頻率表，我們應該透過將所有先前組的頻率新增到當前組的頻率來寫入該組的頻率。

下表顯示了小於累積頻率表的實現。

運動型別	級別	運動員人數	累積頻率
足球	19歲以下	16	16
板球	16歲以下	22	38
羽毛球	14歲以下	30	68
乒乓球	16歲以下	15	83

大於累積頻率表

透過從最高組到最低組計算累積總頻率，可以得到大於累積頻率分佈。

下表顯示了大於累積頻率表的實現。

運動型別	級別	運動員人數	累積頻率
足球	19歲以下	16	83
板球	16歲以下	22	67
羽毛球	14歲以下	30	45
乒乓球	16歲以下	15	15

累積頻率曲線

頻率曲線是頻率分佈曲線，用於顯示離散和連續資料的特性。這些圖比表格資料更能抓住人們的注意力。它使我們更容易比較至少兩個頻率分佈。這兩個頻率分佈的模式和形狀是可以比較的。

累積頻率曲線有兩種型別：

• 小於累積頻率曲線 - 透過繪製小於累積頻率表可以得到此曲線。

• 大於累積頻率曲線 - 透過繪製大於累積頻率表可以得到此曲線。

使用累積頻率曲線查詢中位數

我們可以使用累積頻率曲線來查詢中位數，因此要查詢中位數，我們需要在同一張圖上繪製小於累積頻率曲線和大於累積頻率曲線，這兩條曲線相交的點就是中位數。

已解決示例

示例 1 - 為給定資料製作一個大於累積頻率表。

分數	1-6	7-16	17-25	26-36	37-47	47-60
頻率	2	4	13	18	10	4

解決方案

分數	頻率	累積頻率（大於）
1-6	2	51
7-16	4	49
17-25	13	45
26-36	18	32
37-47	10	14
47-60	4	4

示例 2：使用示例 1 中給出的資料中的累積頻率曲線查詢中位數

解決方案

分數	頻率	累積頻率（大於）	累積頻率（小於）
1-6	2	51	2
7-16	4	49	6
17-25	13	45	19
26-36	18	32	37
37-47	10	14	47
47-60	4	4	51

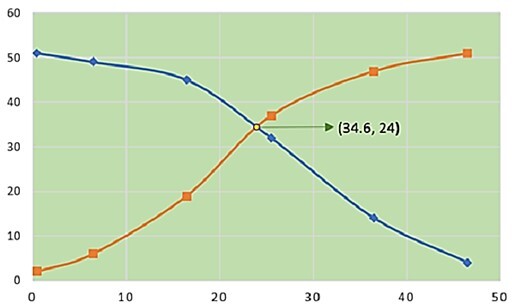
我們可以看到，大於和小於累積頻率曲線在 34.6 頻率處相交。因此，給定資料的中位數是 34.6。

結論

• 中位數是指一組資料中的中間數字或中心值。

• 中位數是三種集中趨勢度量之一。

• 在討論一組資料時，我們會關注資料集中間的位置。這被稱為集中趨勢度量。

• 分組資料的中位數

$$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$$

常見問題

1. 未分組資料中偶數個條目的中位數是多少？

未分組資料中偶數個條目的中位數由以下公式給出：$\mathrm{Median=[\frac{(n+1)}{2}]^{th}}$ term

2. 為什麼使用累積頻率曲線而不是表格來顯示資料？

累積頻率曲線比表格資料更能抓住人們的注意力。它使我們更容易比較至少兩個頻率分佈。

3. 如何使用累積頻率曲線查詢中位數？

在同一張圖上繪製大於和小於累積頻率曲線，這兩條曲線相交的點就是我們的中位數。

4. 分組資料的中位數公式是什麼？

以下公式用於查詢分組資料的中位數$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$

5. 小於累積頻率表是什麼？

要製作小於累積頻率表，請透過將所有先前組的頻率新增到當前組的頻率來寫入該組的頻率。