資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究C++ 中二叉樹的最長之字形路徑
假設我們有一個二叉樹根節點，二叉樹的之字形路徑定義如下：
在二叉樹中選擇任意一個節點和一個方向（向右或向左）。
如果當前方向是向右，則向當前節點的右子節點移動，否則向左子節點移動。
然後將方向從右更改為左，反之亦然。
重複第二步和第三步，直到我們無法在樹中移動。
這裡的之字形長度定義為訪問的節點數減 1。（單個節點的長度為 0）。我們必須找到該樹中包含的最長之字形路徑。例如，如果樹如下所示：
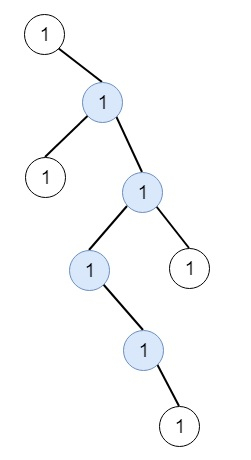
輸出將為 3，因為 (右，左，右)
為了解決這個問題，我們將遵循以下步驟：
定義一個名為 dfs() 的方法，它將接收根節點和 leftB 作為引數
如果根節點為空，則返回 -1
如果根節點是樹中唯一的節點，則返回 0
leftV := dfs(根節點的左子節點, true) 以及 rightV := dfs(根節點的右子節點, false)
ret := ret 和 (1 + leftV 和 rightV 的最大值) 的最大值
如果 leftB 不為 0，則返回 1 + rightV，否則返回 1 + leftV
在主方法中，設定 ret := 0
呼叫 dfs(根節點, true) 和 dfs(根節點, false)
返回 ret
示例（C++）
讓我們看一下以下實現，以便更好地理解：
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
} else {
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
class Solution {
public:
int ret;
int dfs(TreeNode* root, bool leftB){
if(!root) return -1;
if(!root->left && !root->right) return 0;
int leftV = dfs(root->left, true);
int rightV = dfs(root->right, false);
ret = max(ret, 1 + max(leftV, rightV));
if(leftB) return 1 + rightV;
return 1 + leftV;
}
int longestZigZag(TreeNode* root) {
ret = 0;
dfs(root, true);
dfs(root, false);
return ret;
}
};
main(){
vector<int> v = {1,NULL,1,1,1,NULL,NULL,1,1,NULL,1,NULL,NULL,NULL,1,NULL,1};
TreeNode *root = make_tree(v);
Solution ob;
cout << (ob.longestZigZag(root));
}輸入
[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
輸出
3
更新於： 2020-04-29
792 次瀏覽
廣告