資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究Python二叉樹最大路徑和
假設我們有一個非空的二叉樹。我們需要找到路徑和。這裡，路徑是從某個起始節點到任何節點的任何節點序列，其中存在父子連線。路徑必須包含至少一個節點，並且不需要經過根節點。如果輸入樹為：
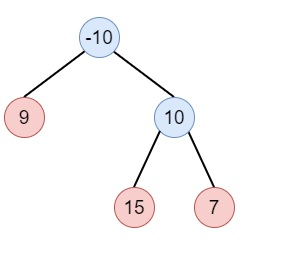
則輸出將為32。
為了解決這個問題，我們將遵循以下步驟：
定義一個名為solve()的方法，它將接收節點作為引數。
如果節點為空或節點的值為0，則返回0。
left := 0和solve(節點的左子節點)中的最大值
right := 0和solve(節點的右子節點)中的最大值
ans := ans和left + right + 節點資料中的最大值
返回節點資料 + left和right中的最大值
在主方法中，設定ans := -inf，然後呼叫solve(root)並返回ans。
示例
讓我們看下面的實現來更好地理解：
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
def insert(temp,data):
que = []
que.append(temp)
while (len(que)):
temp = que[0]
que.pop(0)
if (not temp.left):
if data is not None:
temp.left = TreeNode(data)
else:
temp.left = TreeNode(0)
break
else:
que.append(temp.left)
if (not temp.right):
if data is not None:
temp.right = TreeNode(data)
else:
temp.right = TreeNode(0)
break
else:
que.append(temp.right)
def make_tree(elements):
Tree = TreeNode(elements[0])
for element in elements[1:]:
insert(Tree, element)
return Tree
class Solution(object):
def maxPathSum(self, root):
self.ans = -float('inf')
self.solve(root)
return self.ans
def solve(self,node):
if not node or node.data == 0:
return 0
left = max(0,self.solve(node.left))
right = max(0,self.solve(node.right))
self.ans = max(self.ans,left+right+node.data)
return node.data + max(left,right)
ob = Solution()
root = make_tree([-10,9,10,None,None,15,7])
print(ob.maxPathSum(root))輸入
[-10,9,10,None,None,15,7]
輸出
32
更新於：2020年5月26日
797 次瀏覽
廣告