資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究約瑟夫從一條直線300米道路的一端A跑到另一端B，用時2分30秒，然後轉身往回跑100米到C點，又用時1分鐘。求約瑟夫在（a）從A到B和（b）從A到C的過程中，平均速度和平均速度是多少？
已知
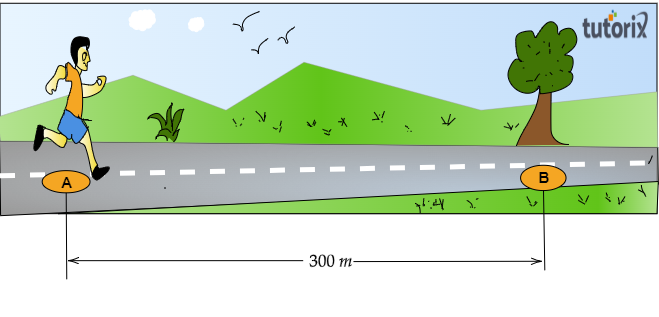
約瑟夫從一條直線300米道路的一端A跑到另一端B，用時2分30秒，然後轉身往回跑100米到C點，又用時1分鐘。
要求
求跑步過程中的平均速度和平均速度 -
$(a)$ 從A到B
$(b)$ 從A到C
解答
$(a)$. 從A到B:
從A到B的總路程 $=300\ 米$
因為道路是直線，約瑟夫沿單一方向跑步，所以
在這種情況下，淨位移為 $300\ 米$。
從A到B所用總時間，$=2\ 分鐘\ 30\ 秒=2\times {60}+30\ 秒=150\ 秒$
因此，從$A\ 到\ B$跑步的平均速度計算如下 -
平均速度$=\frac {總路程}{總時間}$
$=\frac {300}{150}$
$=2\ 米/秒$
平均速度$=\frac {淨位移}{總時間}$
$=\frac {300}{150}$
$=2\ 米/秒$
$(b)$. 從A到C
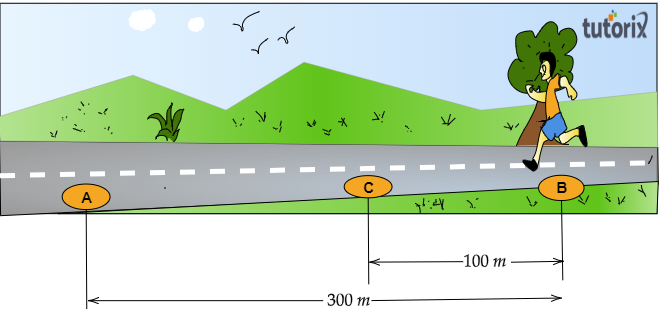
從A到C的總路程 $=$ 從A到B的距離 $+$ 從B到C的距離
$=300\ 米+100\ 米=400\ 米$
淨位移 $=300\ 米-100\ 米=200\ 米$
從A到C的總時間 $=$ 從A到B的時間 + 從B到C的時間
$=150\ 秒+60\ 秒=210\ 秒$
因此，平均速度 $=\frac {總路程}{總時間}$
$=\frac {400}{210}$
$=1.9\ 米/秒$
因此，平均速度 $=\frac {淨位移}{總時間}$
$=\frac {200}{210}$
$=0.95\ 米/秒$
因此，從A到B的平均速度 = 2 米/秒。
從A到B的平均速度 = 2 米/秒。
從A到C的平均速度 = 1.9 米/秒。
從A到C的平均速度 = 0.95 米/秒。
更新時間： 2022年10月10日
210 次瀏覽
廣告