使用或門和與門實現邏輯函式

---

我們可以使用邏輯閘將布林表示式或邏輯函式實現為硬體。使用邏輯閘將邏輯函式實現為硬體的最簡單方法是從輸出開始，向輸入方向移動。

使用邏輯閘實現邏輯函式涉及以特定方式連線不同的邏輯閘。在本文中，我們將把注意力集中在僅使用或門和與門實現邏輯函式上。讓我們從簡要介紹或門和與門開始本文。

什麼是或門？

或門是一種基本邏輯閘。或門可以接受兩個或兩個以上的輸入，但只產生一個輸出。如果任何一個輸入處於高電平（邏輯 1）狀態，則或門輸出高電平（邏輯 1），否則輸出低電平（邏輯 0）。因此，只有當所有輸入都處於低電平（邏輯 0）狀態時，或門的輸出才為低電平或邏輯 0 狀態。

雙輸入或門的邏輯符號如圖 1 所示。

這裡，A 和 B 是或門的輸入，Y 是或門的輸出，因此或門的輸出方程由下式給出：

$$\mathrm{Y=A+B}$$

其中，“+”符號表示或運算。它讀作 Y 等於 A 或 B。

可以透過真值表瞭解或門在不同輸入組合下的工作原理。以下是或門的真值表：

輸入		輸出
A	B	Y = A + B
0	0	0
0	1	1
1	0	1
1	1	1

什麼是與門？

與門是一種基本邏輯閘。與門可以有兩個或兩個以上的輸入，但只產生一個輸出。如果任何一個輸入處於低電平（邏輯 0）狀態，則與門輸出低電平（邏輯 0），否則輸出高電平（邏輯 1）。因此，只有當所有輸入都處於高電平（邏輯 1）狀態時，與門的輸出才為高電平或邏輯 1 狀態。

雙輸入與門的邏輯符號如圖 2 所示。

這裡，A 和 B 是輸入，Y 是與門的輸出變數，則與門的輸出方程由下式給出：

$$\mathrm{Y=A.B}$$

其中，“.”（點）符號表示與運算。它讀作 Y 等於 A 與 B。

可以透過真值表瞭解與門在不同輸入組合下的工作原理。以下是雙輸入與門的真值表：

輸入		輸出
A	B	Y = A . B
0	0	0
0	1	0
1	0	0
1	1	1

現在，讓我們討論一下使用或門和與門實現布林表示式或邏輯函式。

使用或門和與門實現邏輯函式

在本節中，我們將透過示例瞭解使用或門和與門實現邏輯函式。

示例 1

考慮邏輯函式 AB + A + ABC，我們必須使用或門和與門實現此布林表示式。為了實現此邏輯函式，我們將遵循以下步驟：

步驟 1 – 從最終表示式，即輸出開始。我們可以看到邏輯函式中有三個項。因此，我們需要一個三輸入或門。

步驟 2 – 正如我們所看到的，邏輯函式的第一個和第三個項，即 AB 和 ABC 需要與運算。項 AB 需要一個雙輸入與門，而項 ABC 需要一個三輸入與門。

步驟 3 – 最後，透過組合步驟 1 和步驟 2 中實現的硬體，我們得到了給定邏輯函式的完整硬體邏輯實現，如下面的圖所示。

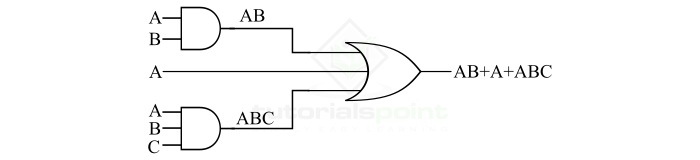
透過這種方式，我們可以輕鬆地使用或門和與門實現邏輯函式。

示例 2

考慮另一個邏輯函式 (A+B).(A+C).(B+C)，我們必須僅使用或門和與門實現此邏輯函式。

透過觀察此邏輯表示式，我們可以解釋說我們需要在最終輸出階段使用一個三輸入與門，以及三個雙輸入或門來實現這三個項。因此，我們可以遵循以下步驟來使用或門和與門實現給定的邏輯函式：

步驟 1 – 實現給定邏輯函式的最終表示式。正如我們所觀察到的，我們可以使用一個三輸入與門來實現它，如下面的圖所示。

步驟 2 – 現在，使用三個雙輸入或門實現給定邏輯函式的三個項，即 (A+B)，(A+C)，(B+C)，如下面的圖所示。

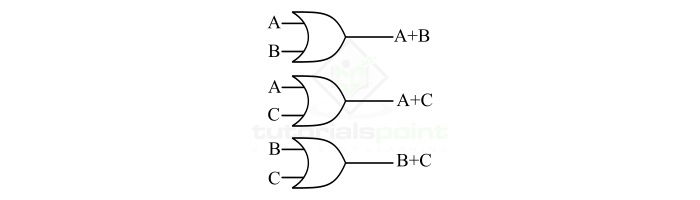
步驟 3 – 最後，透過組合上述兩個步驟的邏輯電路，獲得給定邏輯函式的完整硬體實現。下圖顯示了使用或門和與門實現補碼邏輯函式。

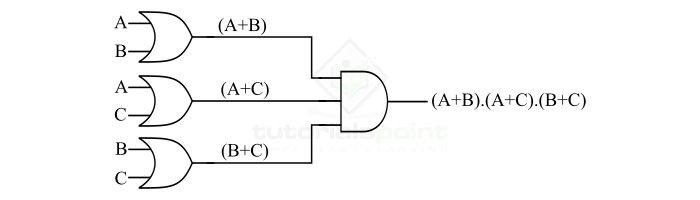
因此，在以上兩個示例中，我們研究了使用或門和與門實現邏輯函式的過程。