遺傳演算法 - 快速指南

遺傳演算法 - 簡介

遺傳演算法 (GA) 是一種基於遺傳和自然選擇原理的搜尋最佳化技術。它常用於尋找複雜問題的最優或近似最優解，而這些問題如果用其他方法解決可能需要花費很長時間。它常用於解決最佳化問題、科研和機器學習。

最佳化簡介

最佳化是指使某件事物變得更好的過程。在任何過程中，我們都有一組輸入和一組輸出，如下圖所示。

最佳化是指以這樣的方式找到輸入的值，以便我們獲得“最佳”輸出值。“最佳”的定義因問題而異，但在數學術語中，它指的是透過改變輸入引數來最大化或最小化一個或多個目標函式。

所有可能的解或輸入可以取的值的集合構成了搜尋空間。在這個搜尋空間中，存在一個點或一組點，它給出了最優解。最佳化的目的是在搜尋空間中找到該點或點集。

什麼是遺傳演算法？

大自然一直是全人類靈感的重要來源。遺傳演算法 (GA) 是基於自然選擇和遺傳概念的基於搜尋的演算法。GA 是一個更大計算分支（稱為進化計算）的一個子集。

GA 由 John Holland 及其在密歇根大學的學生和同事（最著名的是 David E. Goldberg）開發，並且此後已在各種最佳化問題上進行了嘗試，取得了高度成功。

在 GA 中，我們有一個給定問題的可能解的池或種群。然後，這些解經歷重組和變異（就像在自然遺傳中一樣），產生新的後代，並且該過程在各個世代中重複。每個個體（或候選解）都被分配一個適應度值（基於其目標函式值），並且適應性強的個體更有機會交配併產生更多“適應性強”的個體。這與達爾文的“適者生存”理論一致。

這樣，我們就可以在幾代人中不斷“進化”出更好的個體或解決方案，直到我們達到停止標準。

遺傳演算法本質上是隨機的，但它們比隨機區域性搜尋（我們只是嘗試各種隨機解決方案，並跟蹤迄今為止最好的解決方案）的效能要好得多，因為它們也利用歷史資訊。

GA 的優點

GA 具有多種優點，使其廣受歡迎。這些包括 -

不需要任何導數資訊（對於許多現實世界的問題，這些資訊可能不可用）。
與傳統方法相比，速度更快、效率更高。
具有非常好的並行能力。
最佳化連續和離散函式以及多目標問題。
提供一系列“好的”解決方案，而不僅僅是一個解決方案。
始終可以得到問題的答案，並且隨著時間的推移會變得更好。
當搜尋空間非常大並且涉及大量引數時非常有用。

GA 的侷限性

與任何技術一樣，GA 也存在一些侷限性。這些包括 -

GA 不適合所有問題，特別是那些簡單且可以使用導數資訊的問題。
適應度值的計算會重複進行，這對於某些問題來說可能是計算量很大的。
由於是隨機的，因此無法保證解決方案的最優性或質量。
如果實施不當，GA 可能不會收斂到最優解。

GA – 動機

遺傳演算法能夠以“足夠快”的速度提供“足夠好”的解決方案。這使得遺傳演算法在解決最佳化問題方面極具吸引力。GA 需求的原因如下 -

解決難題

在計算機科學中，有一大類問題是NP-Hard。這實質上意味著，即使是最強大的計算系統也需要很長時間（甚至幾年！）才能解決該問題。在這種情況下，GA 被證明是提供可用的近似最優解的有效工具，並且可以在短時間內完成。

基於梯度的方法的失敗

傳統的基於微積分的方法的工作原理是從一個隨機點開始，並沿著梯度的方向移動，直到我們到達山頂。這種技術效率很高，並且非常適用於單峰目標函式（例如線性迴歸中的成本函式）。但是，在大多數現實世界的情況下，我們有一個非常複雜的問題，稱為景觀，它由許多山峰和許多山谷組成，這會導致此類方法失敗，因為它們存在固有的傾向，即陷入區域性最優，如下圖所示。

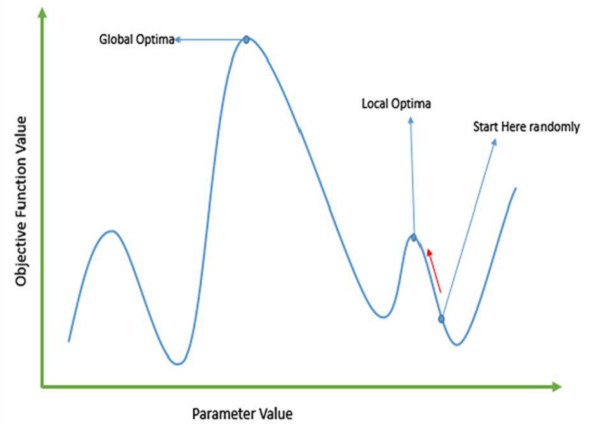
快速獲得良好的解決方案

一些難題，如旅行商問題 (TSP)，具有現實世界的應用，如路徑查詢和 VLSI 設計。現在假設您正在使用 GPS 導航系統，並且它需要幾分鐘（甚至幾小時）才能計算出從源到目的地的“最優”路徑。在這樣的實際應用中，延遲是不可接受的，因此需要“足夠好”的解決方案，並且需要“快速”交付。

遺傳演算法 - 基礎知識

本節介紹理解 GA 所需的基本術語。此外，還以虛擬碼和圖形形式展示了 GA 的通用結構。建議讀者充分理解本節中介紹的所有概念，並在閱讀本教程的其他部分時牢記這些概念。

基本術語

在開始討論遺傳演算法之前，必須熟悉一些基本術語，這些術語將在本教程中使用。

種群 - 它是給定問題所有可能的（編碼）解的一個子集。GA 的種群類似於人類的種群，只是我們用代表人類的候選解代替了人類。
染色體 - 染色體是給定問題的一個解。
基因 - 基因是染色體的一個元素位置。
等位基因 - 它是一個特定染色體基因所取的值。

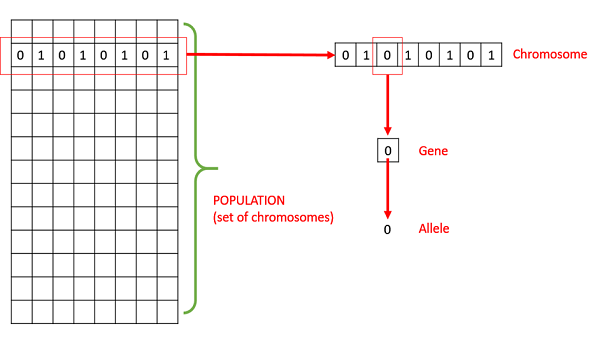
基因型 - 基因型是計算空間中的種群。在計算空間中，解以一種易於理解和使用計算系統進行操作的方式表示。
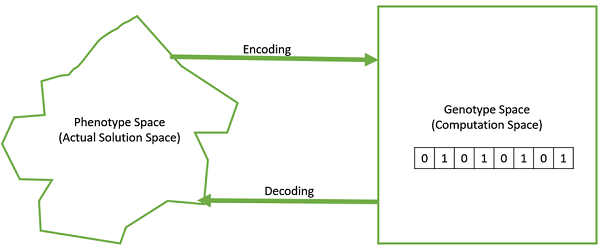
表現型 - 表現型是實際現實世界解空間中的種群，其中解以它們在現實世界中表示的方式表示。
解碼和編碼 - 對於簡單問題，表現型和基因型空間是相同的。但是，在大多數情況下，表現型和基因型空間是不同的。解碼是從基因型到表現型空間轉換解的過程，而編碼是從表現型到基因型空間轉換的過程。解碼應該很快，因為它在 GA 中在適應度值計算期間會重複進行。

例如，考慮 0/1 揹包問題。表現型空間包含僅包含要選擇的專案的專案編號的解決方案。

但是，在基因型空間中，它可以表示為長度為 n 的二進位制字串（其中 n 是專案的數量）。位置 x 處的 0 表示第 x 個專案被選中，而 1 表示相反。這是一種基因型和表現型空間不同的情況。

適應度函式 - 簡單定義的適應度函式是一個函式，它以解作為輸入，併產生解的適用性作為輸出。在某些情況下，適應度函式和目標函式可能相同，而在其他情況下，它可能因問題而異。
遺傳運算元 - 它們改變後代的遺傳組成。這些包括交叉、變異、選擇等。

基本結構

GA 的基本結構如下 -

我們從一個初始種群開始（可以隨機生成或由其他啟發式演算法播種），從該種群中選擇父母進行交配。對父母應用交叉和變異運算元以生成新的後代。最後，這些後代替換種群中的現有個體，並且該過程重複。這樣，遺傳演算法實際上在一定程度上試圖模仿人類進化。

以下每個步驟將在本教程的後面章節中單獨介紹。

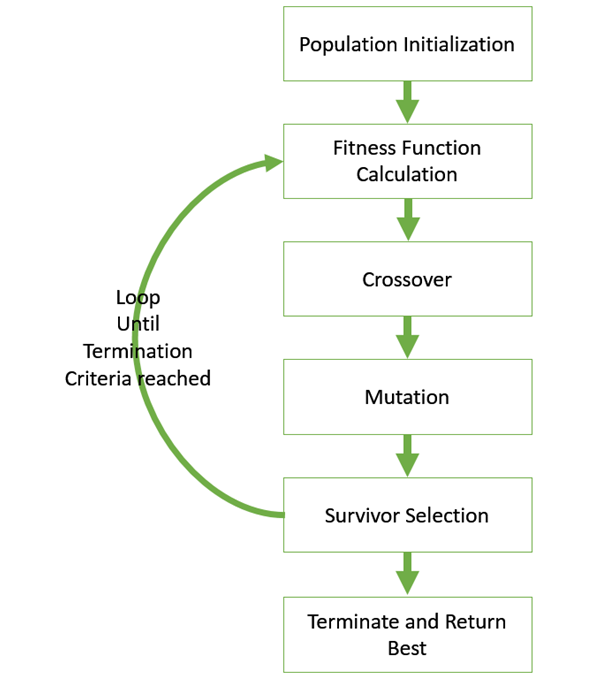
以下程式解釋了 GA 的通用虛擬碼 -

GA()
   initialize population
   find fitness of population
   
   while (termination criteria is reached) do
      parent selection
      crossover with probability pc
      mutation with probability pm
      decode and fitness calculation
      survivor selection
      find best
   return best

基因型表示

在實現遺傳演算法時，最重要的決定之一是決定我們將用於表示解決方案的表示形式。據觀察，不正確的表示會導致 GA 效能下降。

因此，選擇合適的表示方法，並對錶型和基因型空間之間的對映進行恰當的定義，對於遺傳演算法的成功至關重要。

在本節中，我們將介紹一些遺傳演算法中最常用的表示方法。但是，表示方法高度依賴於具體問題，讀者可能會發現其他表示方法或此處提到的表示方法的組合可能更適合他的問題。

二進位制表示

這是遺傳演算法中最簡單和最廣泛使用的表示方法之一。在這種表示方法中，基因型由位串組成。

對於某些問題，當解空間由布林決策變數（是或否）組成時，二進位制表示是自然的。例如，考慮0/1揹包問題。如果有n個物品，我們可以用一個n個元素的二進位制字串來表示一個解，其中第x個元素表示是否選擇物品x（1）或不選擇（0）。

對於其他問題，特別是那些處理數字的問題，我們可以用它們的二進位制表示來表示這些數字。這種編碼的問題在於不同的位具有不同的意義，因此變異和交叉運算元可能產生不希望的結果。這可以透過使用**格雷碼**在一定程度上解決，因為一位的變化不會對解產生重大影響。

實值表示

對於我們希望使用連續變數而不是離散變數來定義基因的問題，實值表示是最自然的。然而，這些實值或浮點數的精度受限於計算機。

整數表示

對於離散值基因，我們不能總是將解空間限制為二進位制的“是”或“否”。例如，如果我們想編碼四個方向——北、南、東和西，我們可以將它們編碼為**{0,1,2,3}**。在這種情況下，整數表示是可取的。

排列表示

在許多問題中，解由元素的順序表示。在這種情況下，排列表示是最合適的。

這種表示法的經典示例是旅行商問題（TSP）。在這種問題中，旅行商必須對所有城市進行巡迴，每個城市恰好訪問一次，並返回到起始城市。巡迴的總距離必須最小化。TSP的解自然地是所有城市的排序或排列，因此對這個問題使用排列表示是有意義的。

遺傳演算法 - 種群

種群是當前代中解的一個子集。它也可以定義為一組染色體。在處理遺傳演算法種群時，需要牢記以下幾點：

應保持種群的多樣性，否則可能會導致過早收斂。
種群規模不應過大，因為它會導致遺傳演算法速度變慢，而較小的種群可能不足以形成良好的交配池。因此，需要透過反覆試驗來確定最佳種群規模。

種群通常定義為一個二維陣列——**種群規模，染色體長度，基因長度**。

種群初始化

在遺傳演算法中初始化種群主要有兩種方法：

**隨機初始化**——用完全隨機的解填充初始種群。
**啟發式初始化**——使用已知的啟發式方法填充初始種群。

觀察發現，不應該使用啟發式方法初始化整個種群，因為它會導致種群具有相似的解並且多樣性很小。實驗觀察表明，隨機解是推動種群達到最優性的因素。因此，對於啟發式初始化，我們只用幾個好的解來填充種群，其餘的用隨機解填充，而不是用基於啟發式的解填充整個種群。

還觀察到，在某些情況下，啟發式初始化只會影響種群的初始適應度，但最終，導致最優性的是解的多樣性。

種群模型

兩種廣泛使用的種群模型：

穩態

在穩態遺傳演算法中，我們在每次迭代中生成一個或兩個後代，並用它們替換種群中的一個或兩個個體。穩態遺傳演算法也稱為**增量遺傳演算法**。

代際

在代際模型中，我們生成'n'個後代，其中n是種群規模，並在迭代結束時用新種群替換整個種群。

遺傳演算法 - 適應度函式

簡單來說，適應度函式是一個函式，它**以問題的候選解作為輸入，並輸出**該解相對於所考慮問題的“適應度”或“優劣”。

在遺傳演算法中，適應度值的計算會反覆進行，因此它應該足夠快。適應度值的緩慢計算會對遺傳演算法產生不利影響，使其異常緩慢。

在大多數情況下，適應度函式和目標函式相同，因為目標是最大化或最小化給定的目標函式。但是，對於具有多個目標和約束的更復雜的問題，**演算法設計者**可能會選擇使用不同的適應度函式。

適應度函式應具有以下特徵：

適應度函式的計算速度應足夠快。
它必須定量地衡量給定解的適應度或從給定解可以產生多適應的個體。

在某些情況下，由於手頭問題的固有複雜性，可能無法直接計算適應度函式。在這種情況下，我們會進行適應度近似以滿足我們的需求。

下圖顯示了0/1揹包問題解的適應度計算。這是一個簡單的適應度函式，它只將被選擇的物品（值為1）的利潤值加起來，從左到右掃描元素，直到揹包裝滿。

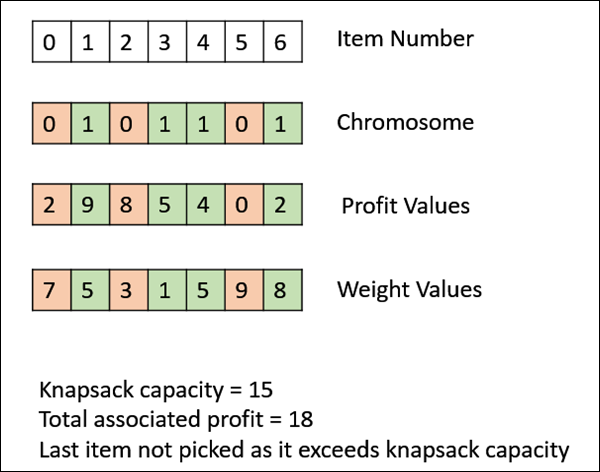
遺傳演算法 - 親本選擇

親本選擇是選擇交配並重組以建立下一代後代的親本的過程。親本選擇對遺傳演算法的收斂速度至關重要，因為好的親本會將個體引導到更好、更適應的解。

但是，應注意防止一個極其適應的解在幾代中接管整個種群，因為這會導致解在解空間中彼此靠近，從而導致多樣性喪失。**保持種群良好的多樣性**對於遺傳演算法的成功至關重要。一個極其適應的解接管整個種群的情況稱為**過早收斂**，這是遺傳演算法中不希望出現的情況。

適應度比例選擇

適應度比例選擇是最流行的親本選擇方法之一。在這種方法中，每個個體成為親本的機率與其適應度成正比。因此，適應性強的個體有更高的機會交配並將它們的特徵傳播到下一代。因此，這種選擇策略對種群中適應性強的個體施加選擇壓力，隨著時間的推移進化出更好的個體。

考慮一個圓形輪盤。輪盤被分成**n塊**，其中n是種群中個體的數量。每個個體獲得圓形輪盤的一部分，這部分與它的適應度值成正比。

適應度比例選擇有兩種可能的實現方式：

輪盤賭選擇

在輪盤賭選擇中，圓形輪盤如前所述進行劃分。在輪盤圓周上選擇一個固定點，如圖所示，並旋轉輪盤。輪盤中位於固定點前面的區域被選為親本。對於第二個親本，重複相同的過程。

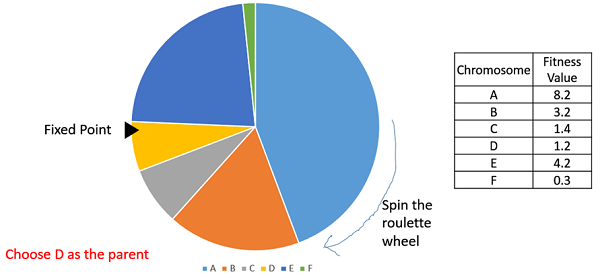
很明顯，適應性強的個體在輪盤上佔據更大的扇形區域，因此在輪盤旋轉時落到固定點前面的機率更大。因此，選擇個體的機率直接取決於其適應度。

在實現方面，我們使用以下步驟：

計算S = 適應度之和。
生成一個介於0和S之間的隨機數。
從種群的頂部開始，將適應度不斷新增到部分和P中，直到P
P超過S的個體是被選擇的個體。

隨機均勻抽樣（SUS）

隨機均勻抽樣與輪盤賭選擇非常相似，但是，我們不是隻有一個固定點，而是有多個固定點，如下面的圖片所示。因此，所有親本都在輪盤的一次旋轉中被選中。此外，這種設定鼓勵高度適應的個體至少被選中一次。

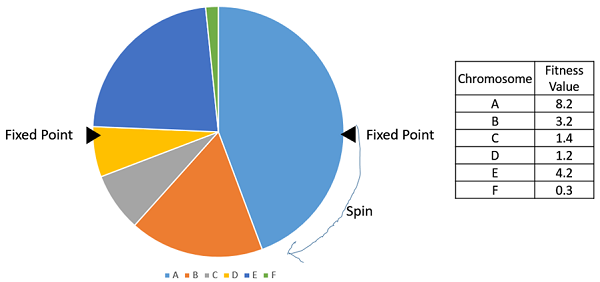
需要注意的是，適應度比例選擇方法不適用於適應度可以取負值的情況。

錦標賽選擇

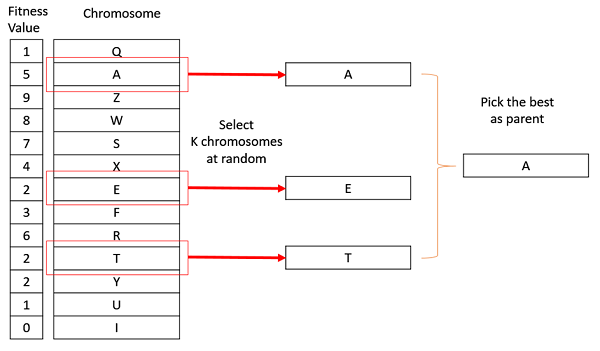
在K路錦標賽選擇中，我們從種群中隨機選擇K個個體，並從中選擇最好的個體作為親本。重複相同的過程以選擇下一個親本。錦標賽選擇在文獻中也非常流行，因為它甚至可以處理負適應度值。

等級選擇

等級選擇也可以處理負適應度值，並且主要用於種群中個體具有非常接近的適應度值的情況（通常發生在執行結束時）。這導致每個個體幾乎擁有相同比例的扇形區域（如適應度比例選擇的情況），因此每個個體無論其相對適應度如何，都具有大致相同的被選為親本的機率。這反過來會導致對適應性強的個體的選擇壓力減弱，使遺傳演算法在這種情況下進行較差的親本選擇。

在這種方法中，我們在選擇親本時去除了適應度值的概念。但是，種群中的每個個體都根據其適應度進行排序。親本的選擇取決於每個個體的等級，而不是適應度。等級較高的個體比等級較低的個體更受青睞。

染色體	適應度值	等級
A	8.1	1
B	8.0	4
C	8.05	2
D	7.95	6
E	8.02	3
F	7.99	5

隨機選擇

在本策略中，我們從現有種群中隨機選擇父母。沒有針對更適應個體的選擇壓力，因此通常避免使用此策略。

遺傳演算法 - 交叉

在本章中，我們將討論交叉運算元及其其他模組、用途和益處。

交叉介紹

交叉運算元類似於生物繁殖和生物交叉。在這種情況下，選擇多個父母，並使用父母的遺傳物質產生一個或多個後代。交叉通常以高機率應用於遺傳演算法 – p_c 。

交叉運算元

在本節中，我們將討論一些最常用的交叉運算元。需要注意的是，這些交叉運算元非常通用，遺傳演算法設計者也可以選擇實現特定於問題的交叉運算元。

單點交叉

在這種單點交叉中，選擇一個隨機的交叉點，並交換其兩個父代的尾部以獲得新的後代。

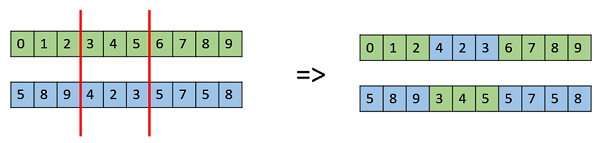
多點交叉

多點交叉是單點交叉的推廣，其中交替片段被交換以獲得新的後代。

均勻交叉

在均勻交叉中，我們不將染色體分成片段，而是單獨處理每個基因。在這種情況下，我們實際上為每個染色體拋硬幣，以決定它是否包含在後代中。我們還可以偏向一個父代，使孩子從該父代那裡獲得更多的遺傳物質。

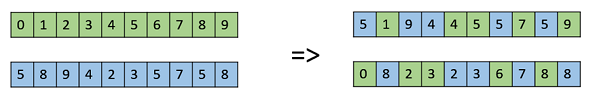
整體算術重組

這通常用於整數表示，並透過使用以下公式取兩個父代的加權平均值來工作：

子代1 = α.x + (1-α).y
子代2 = α.x + (1-α).y

顯然，如果 α = 0.5，則兩個子代將完全相同，如下面的影像所示。

Davis'順序交叉 (OX1)

OX1 用於基於排列的交叉，目的是將有關相對順序的資訊傳遞給後代。其工作原理如下：

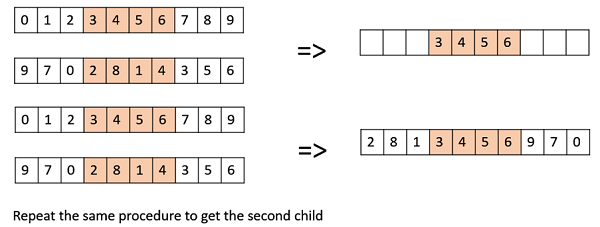
在父代中建立兩個隨機交叉點，並將它們之間的片段從第一個父代複製到第一個後代。
現在，從第二個父代的第二個交叉點開始，將第二個父代中剩餘的未使用數字複製到第一個子代，環繞列表。
對第二個子代重複此操作，並交換父代的角色。

還存在許多其他交叉，例如部分對映交叉 (PMX)、基於順序的交叉 (OX2)、洗牌交叉、環交叉等。

遺傳演算法 - 變異

變異介紹

簡單來說，變異可以定義為染色體中一個小的隨機調整，以獲得新的解。它用於維持和引入遺傳種群的多樣性，並且通常以低機率應用 – p_m。如果機率非常高，則遺傳演算法會簡化為隨機搜尋。

變異是遺傳演算法中與搜尋空間“探索”相關的一部分。據觀察，變異對於遺傳演算法的收斂至關重要，而交叉則不然。

變異運算元

在本節中，我們將描述一些最常用的變異運算元。與交叉運算元一樣，這不是一個詳盡的列表，遺傳演算法設計者可能會發現這些方法的組合或特定於問題的變異運算元更有用。

位翻轉變異

在這種位翻轉變異中，我們選擇一個或多個隨機位並將其翻轉。這用於二進位制編碼的遺傳演算法。

隨機重置

隨機重置是位翻轉對於整數表示的擴充套件。在這種情況下，從允許值的集合中隨機選擇一個值並將其分配給隨機選擇的基因。

交換變異

在交換變異中，我們隨機選擇染色體上的兩個位置，並交換其值。這在基於排列的編碼中很常見。

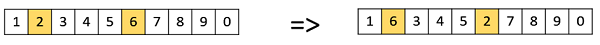
擾亂變異

擾亂變異在基於排列的表示中也很流行。在這種情況下，從整個染色體中選擇一個基因子集，並隨機擾亂或洗牌其值。

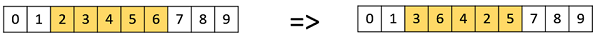
倒位變異

在倒位變異中，我們像在擾亂變異中一樣選擇一個基因子集，但不是洗牌子集，而只是反轉子集中的整個字串。

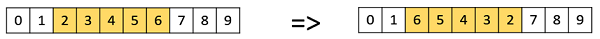
遺傳演算法 - 倖存者選擇

倖存者選擇策略決定哪些個體將被淘汰，哪些個體將在下一代中保留。它至關重要，因為它應該確保更適應的個體不會被淘汰出種群，同時也要在種群中保持多樣性。

一些遺傳演算法採用精英策略。簡單來說，這意味著種群中當前最適應的成員總是被傳播到下一代。因此，在任何情況下，當前種群中最適應的成員都不能被替換。

最簡單的策略是將種群中的隨機成員淘汰，但這種方法經常存在收斂問題，因此廣泛使用以下策略。

基於年齡的選擇

在基於年齡的選擇中，我們沒有適應度的概念。它基於這樣一個前提：每個個體都被允許在種群中存在有限的世代，在此期間它可以繁殖，之後，它將被淘汰出種群，無論其適應度有多好。

例如，在下面的示例中，年齡是個體在種群中存在的世代數。種群中最老的成員，即 P4 和 P7，被淘汰出種群，其餘成員的年齡增加 1。

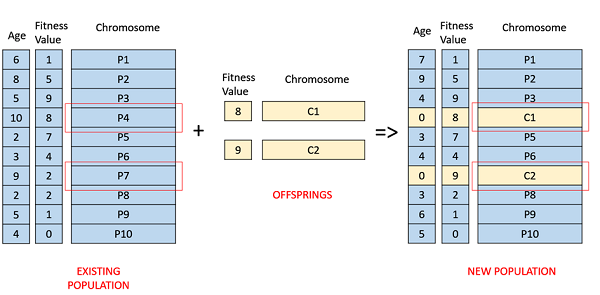
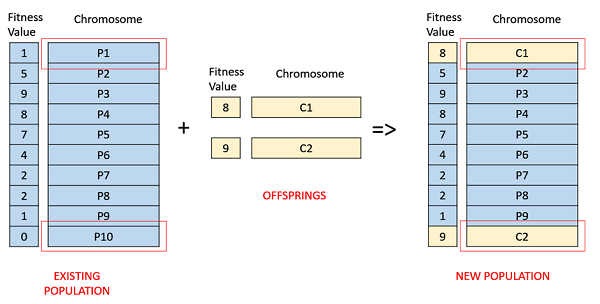
基於適應度的選擇

在這種基於適應度的選擇中，子代傾向於替換種群中最不適應的個體。最不適應個體的選擇可以使用前面描述的任何選擇策略的變體完成 - 錦標賽選擇、適應度比例選擇等。

例如，在下面的影像中，子代替換了種群中最不適應的個體 P1 和 P10。需要注意的是，由於 P1 和 P9 的適應度值相同，因此決定從種群中刪除哪個個體是任意的。

遺傳演算法 - 終止條件

遺傳演算法的終止條件對於確定遺傳演算法執行何時結束非常重要。據觀察，最初，遺傳演算法進展非常快，每隔幾個迭代就會出現更好的解，但這在後期往往會趨於飽和，改進非常小。我們通常希望終止條件使得我們的解在執行結束時接近最優解。

通常，我們會保留以下終止條件之一：

當種群在 X 次迭代中沒有改進時。
當我們達到絕對的世代數時。
當目標函式值達到某個預定義值時。

例如，在遺傳演算法中，我們保留一個計數器，跟蹤種群沒有改進的世代數。最初，我們將此計數器設定為零。每次我們沒有生成比種群中個體更好的後代時，我們都會增加計數器。

但是，如果任何後代的適應度更好，那麼我們將計數器重置為零。當計數器達到預定值時，演算法終止。

與遺傳演算法的其他引數一樣，終止條件也高度特定於問題，遺傳演算法設計者應該嘗試各種選項，以瞭解哪種選項最適合其特定問題。

終身適應模型

到目前為止，在本教程中，我們討論的內容都對應於達爾文進化模型 - 自然選擇以及透過重組和變異產生的遺傳變異。在自然界中，只有個體基因型中包含的資訊可以傳遞給下一代。這是我們迄今為止在教程中一直在遵循的方法。

然而，也存在其他終生適應模型 - 拉馬克模型和鮑爾德溫模型。需要注意的是，哪種模型最好，存在爭議，研究人員獲得的結果表明，終生適應的選擇高度特定於問題。

通常，我們會將遺傳演算法與區域性搜尋混合 - 例如在模因演算法中。在這種情況下，人們可能會選擇使用拉馬克模型或鮑爾德溫模型來決定對區域性搜尋後生成的個體進行什麼操作。

拉馬克模型

拉馬克模型本質上說的是，個體在其一生中獲得的特徵可以遺傳給其後代。它以法國生物學家讓-巴蒂斯特·拉馬克命名。

儘管自然生物學完全摒棄了拉馬克主義，因為我們都知道只有基因型中的資訊可以傳遞。然而，從計算的角度來看，已經表明，採用拉馬克模型對於某些問題可以獲得良好的結果。

在拉馬克模型中，區域性搜尋運算元檢查鄰域（獲得新特徵），如果找到更好的染色體，它將成為後代。

鮑爾德溫模型

鮑爾德溫模型是一箇中間思想，由詹姆斯·馬克·鮑爾德溫 (1896) 命名。在鮑爾德溫模型中，染色體可以編碼學習有益行為的傾向。這意味著，與拉馬克模型不同，我們不會將獲得的特徵傳遞給下一代，也不會像在達爾文模型中那樣完全忽略獲得的特徵。

鮑爾德溫模型處於這兩個極端之間，其中編碼了個體獲得某些特徵的傾向，而不是特徵本身。

在這個鮑爾德溫模型中，區域性搜尋運算元檢查鄰域（獲得新特徵），如果找到更好的染色體，它只會將改進的適應度分配給染色體，而不會修改染色體本身。適應度的變化表示染色體“獲得特徵”的能力，即使它沒有直接傳遞給後代。

有效實施

遺傳演算法本質上非常通用，僅僅將其應用於任何最佳化問題都不會產生良好的結果。在本節中，我們將描述一些可以幫助和協助遺傳演算法設計者或遺傳演算法實施者工作的要點。

引入特定於問題的領域知識

據觀察，我們向遺傳演算法中整合的特定於問題的領域知識越多，我們獲得的目標值就越好。可以透過使用特定於問題的交叉或變異運算元、自定義表示等來新增特定於問題的資訊。

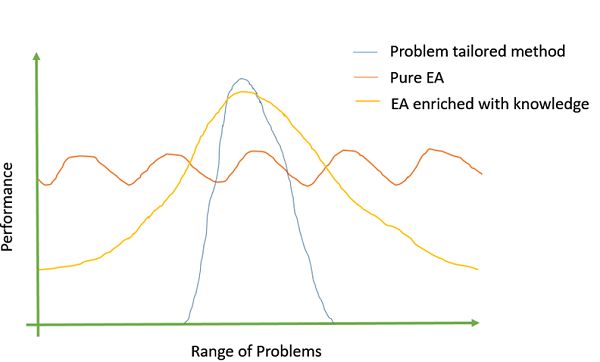
下圖顯示了 Michalewicz (1990) 對 EA 的看法：

減少擁擠

擁擠發生在一個適應性很強的染色體大量繁殖時，在幾代之後，整個種群都充滿了具有相似適應度的相似解。這降低了多樣性，而多樣性是確保遺傳演算法成功的非常重要的因素。有很多方法可以限制擁擠。其中一些是：

變異以引入多樣性。
切換到等級選擇和錦標賽選擇，與適應度比例選擇相比，它們對適應度相似的個體施加了更大的選擇壓力。
適應度共享 - 在此，如果種群中已經存在類似的個體，則個體的適應度會降低。

隨機化有幫助！

實驗觀察表明，最佳解決方案是由隨機化的染色體驅動的，因為它們為種群帶來了多樣性。遺傳演算法的實現者應該注意在種群中保持足夠的隨機性和多樣性，以獲得最佳結果。

將遺傳演算法與區域性搜尋混合

區域性搜尋是指檢查給定解鄰域內的解，以尋找更好的目標值。

有時將遺傳演算法與區域性搜尋混合起來可能很有用。下圖顯示了在遺傳演算法中可以引入區域性搜尋的各種位置。

引數和技術的變異

在遺傳演算法中，沒有“一刀切”或適用於所有問題的萬能公式。即使在初始遺傳演算法準備就緒後，也需要花費大量時間和精力來調整引數（如種群大小、變異和交叉機率等），以找到適合特定問題的引數。

遺傳演算法 - 高階主題

在本節中，我們將介紹遺傳演算法中的一些高階主題。僅尋求遺傳演算法入門介紹的讀者可以選擇跳過本節。

約束最佳化問題

約束最佳化問題是指那些必須最大化或最小化給定目標函式值且受某些約束條件限制的最佳化問題。因此，並非解空間中的所有結果都是可行的，解空間包含如下所示的可行區域。

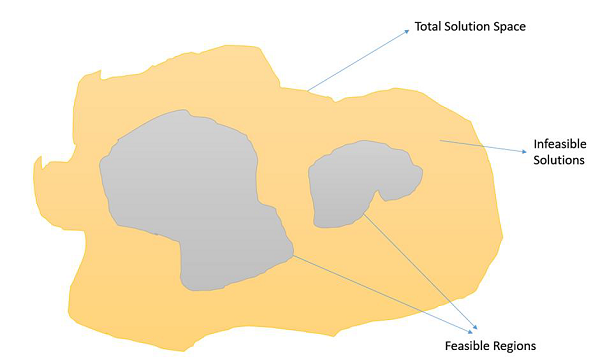
在這種情況下，交叉和變異運算元可能會給我們一些不可行的解。因此，在處理約束最佳化問題時，必須在遺傳演算法中採用其他機制。

一些最常見的方法是 -

使用懲罰函式，降低不可行解的適應度，最好是使適應度與違反的約束條件數量或偏離可行區域的距離成比例地降低。
使用修復函式，接受不可行解並對其進行修改，以滿足違反的約束條件。
不允許不可行解進入種群。
使用特殊的表示或解碼函式，確保解的可行性。

基本理論背景

在本節中，我們將討論模式定理和NFL定理以及構建塊假設。

模式定理

研究人員一直在試圖弄清楚遺傳演算法工作背後的數學原理，而Holland的模式定理是朝著這個方向邁出的一步。多年來，人們對模式定理進行了各種改進和建議，使其更加通用。

在本節中，我們不會深入探討模式定理的數學原理，而是嘗試對模式定理是什麼有一個基本的瞭解。需要了解的基本術語如下 -

模式是一個“模板”。正式地，它是在字母表 = {0,1,*} 上的字串，

其中*表示“不關心”，可以取任何值。

因此，*10*1可以表示01001、01011、11001或11011

在幾何上，模式是解搜尋空間中的超平面。
模式的階是指基因中指定固定位置的數量。

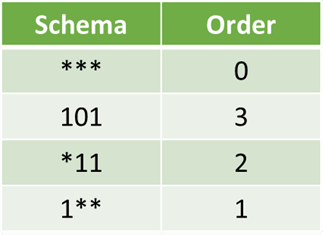
定義長度是指基因中兩個最遠固定符號之間的距離。

模式定理指出，具有高於平均適應度、較短定義長度和較低階的模式更有可能在交叉和變異中存活下來。

構建塊假設

構建塊是具有上述給定平均適應度的低階、低定義長度的模式。構建塊假設認為，這樣的構建塊是遺傳演算法成功和適應的基礎，因為它透過依次識別和重組這些“構建塊”而逐步發展。

沒有免費午餐（NFL）定理

Wolpert和Macready在1997年發表了一篇題為“最佳化問題的無免費午餐定理”的論文。它本質上指出，如果我們對所有可能問題的空間進行平均，那麼所有非重複訪問的黑盒演算法都將表現出相同的效能。

這意味著，我們對問題的瞭解越多，我們的遺傳演算法就越針對特定問題，並且效能越好，但它會透過在其他問題上表現不佳來彌補這一點。

基於遺傳演算法的機器學習

遺傳演算法也應用於機器學習。分類器系統是一種基於遺傳的機器學習（GBML）系統，在機器學習領域經常使用。GBML方法是機器學習的一種利基方法。

GBML系統有兩類 -

匹茲堡方法 - 在這種方法中，一個染色體編碼一個解，因此適應度分配給解。
密歇根方法 - 一個解通常由多個染色體表示，因此適應度分配給部分解。

應該記住，標準問題（如交叉、變異、拉馬克式或達爾文式等）也存在於GBML系統中。

遺傳演算法 - 應用領域

遺傳演算法主要用於各種最佳化問題，但它們也經常用於其他應用領域。

在本節中，我們列出了遺傳演算法經常使用的一些領域。它們是 -

最佳化 - 遺傳演算法最常用於最佳化問題，在這些問題中，我們必須在給定的一組約束條件下最大化或最小化給定的目標函式值。解決最佳化問題的方案已在整個教程中進行了強調。
經濟學 - 遺傳演算法還用於表徵各種經濟模型，如蛛網模型、博弈論均衡求解、資產定價等。
神經網路 - 遺傳演算法還用於訓練神經網路，特別是迴圈神經網路。
並行化 - 遺傳演算法還具有非常好的並行能力，並且證明是解決某些問題的非常有效的方法，並且還為研究提供了一個很好的領域。
影像處理 - 遺傳演算法也用於各種數字影像處理（DIP）任務，如密集畫素匹配。
車輛路徑問題 - 具有多個軟時間視窗、多個貨運站和異構車隊。
排程應用 - 遺傳演算法也用於解決各種排程問題，特別是時間表問題。
機器學習 - 正如已經討論過的，基於遺傳的機器學習（GBML）是機器學習中的一個利基領域。
機器人軌跡生成 - 遺傳演算法已被用於規劃機器人手臂從一點移動到另一點所採取的路徑。
飛機引數設計 - 遺傳演算法已被用於透過改變引數和發展更好的解決方案來設計飛機。
DNA分析 - 遺傳演算法已被用於使用樣品的質譜資料來確定DNA的結構。
多模態最佳化 - 遺傳演算法顯然是多模態最佳化的非常好的方法，在多模態最佳化中，我們必須找到多個最優解。
旅行商問題及其應用 - 遺傳演算法已被用於解決TSP問題，這是一個使用新穎的交叉和打包策略的著名組合問題。

遺傳演算法 - 進一步閱讀

以下書籍可供參考，以進一步提高讀者對遺傳演算法和進化計算的瞭解 -

David E. Goldberg著《搜尋、最佳化和機器學習中的遺傳演算法》。
Zbigniew Michalewicz著《遺傳演算法 + 資料結構 = 進化程式》。
Randy L. Haupt和Sue Ellen Haupt著《實用遺傳演算法》。
Kalyanmoy Deb著《使用進化演算法的多目標最佳化》。

列印頁面