
- 遺傳演算法教程
- 遺傳演算法 – 首頁
- 遺傳演算法 – 簡介
- 遺傳演算法 – 基礎
- 基因型表示
- 遺傳演算法 – 種群
- 遺傳演算法 – 適應度函式
- 遺傳演算法 - 親本選擇
- 遺傳演算法 – 交叉
- 遺傳演算法 – 變異
- 倖存者選擇
- 終止條件
- 終身適應模型
- 有效實施
- 高階主題
- 應用領域
- 進一步閱讀
- 遺傳演算法資源
- 遺傳演算法 - 快速指南
- 遺傳演算法 - 資源
- 遺傳演算法 - 討論
遺傳演算法 - 親本選擇
親本選擇是選擇進行交配並重組以建立下一代後代的父母的過程。親本選擇對於 GA 的收斂速度至關重要,因為優秀的父母會將個體引導到更好、更適合的解決方案。
但是,應注意防止一個極其適合的解決方案在幾代人中接管整個種群,因為這會導致解決方案在解決方案空間中彼此靠近,從而導致多樣性喪失。保持良好的多樣性對於 GA 的成功至關重要。一個極其適合的解決方案接管整個種群的情況稱為過早收斂,這是 GA 中不希望出現的情況。
適應度比例選擇
適應度比例選擇是最流行的親本選擇方法之一。在這種方法中,每個個體成為父母的機率與其適應度成正比。因此,適應度更高的個體具有更高的交配機會,並將它們的特徵傳播到下一代。因此,這種選擇策略對種群中適應度更高的個體施加選擇壓力,隨著時間的推移逐漸進化出更優秀的個體。
考慮一個圓形輪子。該輪子被分成n 個扇形,其中 n 是種群中個體的數量。每個個體獲得圓形的一部分,這部分與其適應度值成正比。
適應度比例選擇有兩種實現方式:
輪盤賭選擇
在輪盤賭選擇中,圓形輪子如前所述進行劃分。在輪子圓周上選擇一個固定點,如圖所示,然後旋轉輪子。輪子前面出現的區域被選為親本。對於第二個親本,重複相同的過程。
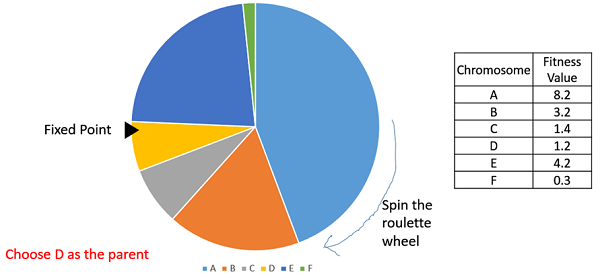
很明顯,適應度更高的個體在輪子上擁有更大的扇形,因此當輪子旋轉時,它更有可能落在固定點前面。因此,選擇個體的機率直接取決於其適應度。
從實現的角度來看,我們使用以下步驟:
計算 S = 適應度的總和。
生成一個介於 0 和 S 之間的隨機數。
從種群的頂部開始,不斷將適應度新增到部分和 P 中,直到 P<S。
P 超過 S 的個體是被選中的個體。
隨機通用抽樣 (SUS)
隨機通用抽樣與輪盤賭選擇非常相似,但是,它不是隻有一個固定點,而是有多個固定點,如以下影像所示。因此,所有父母都在一次旋轉輪子中被選中。此外,這種設定鼓勵高度適應的個體至少被選中一次。
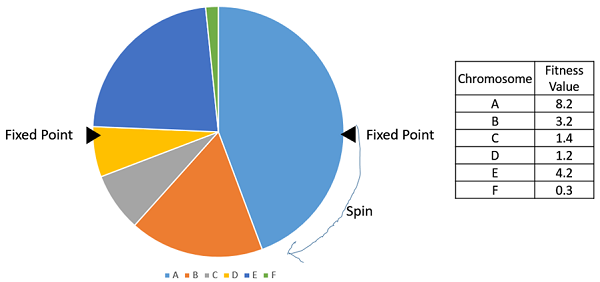
需要注意的是,適應度比例選擇方法不適用於適應度可以取負值的情況。
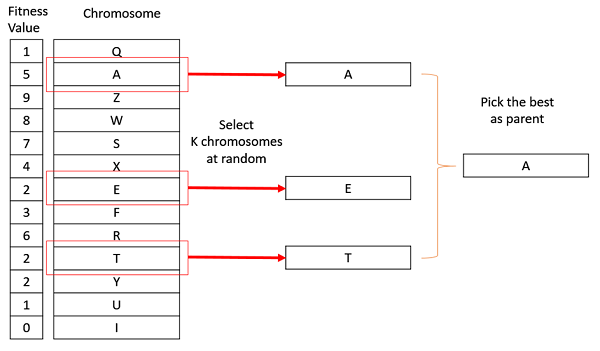
錦標賽選擇
在 K 路錦標賽選擇中,我們從種群中隨機選擇 K 個個體,並選擇其中最好的個體作為親本。重複相同的過程以選擇下一個親本。錦標賽選擇在文獻中也極其流行,因為它甚至可以處理負適應度值。
等級選擇
等級選擇也適用於負適應度值,並且主要用於種群中個體具有非常接近的適應度值的情況(這通常發生在執行結束時)。這導致每個個體幾乎擁有相同的扇形比例(如適應度比例選擇的情況),因此每個個體無論其相對適應度如何,都具有大致相同的被選為親本的機率。這反過來會導致對適應度更高個體的選擇壓力降低,導致 GA 在此類情況下做出糟糕的親本選擇。

在這種方法中,我們在選擇親本時去除了適應度值的概念。但是,種群中的每個個體都根據其適應度進行排名。親本的選擇取決於每個個體的排名,而不是適應度。排名更高的個體比排名較低的個體更受歡迎。
| 染色體 | 適應度值 | 等級 |
|---|---|---|
| A | 8.1 | 1 |
| B | 8.0 | 4 |
| C | 8.05 | 2 |
| D | 7.95 | 6 |
| E | 8.02 | 3 |
| F | 7.99 | 5 |
隨機選擇
在這種策略中,我們從現有種群中隨機選擇親本。對適應度更高的個體沒有選擇壓力,因此通常避免使用這種策略。