遺傳演算法 - 高階主題

在本節中，我們將介紹遺傳演算法中的一些高階主題。只想瞭解遺傳演算法基礎知識的讀者可以選擇跳過本節。

約束最佳化問題

約束最佳化問題是指那些需要在滿足某些約束條件下最大化或最小化給定目標函式值的問題。因此，並非解空間中的所有結果都是可行的，解空間包含可行區域，如下圖所示。

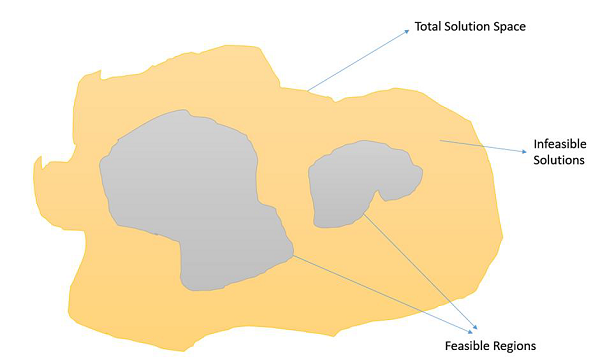
在這種情況下，交叉和變異運算元可能會給我們不可行的解。因此，在處理約束最佳化問題時，必須在遺傳演算法中採用其他機制。

一些最常用的方法是：

• 使用懲罰函式，降低不可行解的適應度，最好是使適應度隨著違反約束的數量或與可行區域的距離成比例地降低。

• 使用修復函式，將不可行解修改為滿足違反的約束條件。

• 不允許不可行解進入種群。

• 使用特殊的表示或解碼函式，以確保解的可行性。

基本理論背景

在本節中，我們將討論模式定理和NFL定理以及構建塊假設。

模式定理

研究人員一直在試圖弄清楚遺傳演算法工作背後的數學原理，而Holland的模式定理是朝著這個方向邁出的一步。多年來，對模式定理進行了各種改進和建議，使其更具通用性。

在本節中，我們不會深入探討模式定理的數學原理，而是試圖對模式定理是什麼有一個基本的理解。需要了解的基本術語如下：

• 模式是一個“模板”。形式上，它是在字母表 = {0,1,*} 上的一個字串，

  其中*是萬用字元，可以取任何值。

  因此，*10*1可以表示01001、01011、11001或11011

  幾何上，模式是解搜尋空間中的超平面。

• 模式的階是基因中指定固定位置的數量。

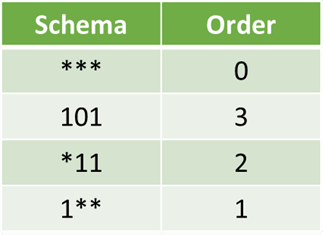
• 定義長度是基因中兩個最遠固定符號之間的距離。

模式定理指出，具有高於平均適應度、較短定義長度和較低階的模式更有可能在交叉和變異中存活下來。

構建塊假設

構建塊是具有高於平均適應度的低階、低定義長度模式。構建塊假設認為，隨著遺傳演算法的進行，透過逐步識別和重新組合這些“構建塊”，這些構建塊構成了遺傳演算法成功和適應的基礎。

沒有免費午餐(NFL)定理

Wolpert和Macready在1997年發表了一篇題為“最佳化問題的無免費午餐定理”的論文。它本質上指出，如果我們對所有可能問題的空間進行平均，那麼所有非重複訪問黑盒演算法都將表現出相同的效能。

這意味著，我們對問題的瞭解越多，我們的遺傳演算法就越針對特定問題，並且效能越好，但它會透過在其他問題上的表現不佳來彌補這一點。

基於遺傳演算法的機器學習

遺傳演算法也應用於機器學習。分類器系統是一種經常用於機器學習領域的基於遺傳的機器學習(GBML)系統。GBML方法是機器學習的一種利基方法。

GBML系統分為兩類：

• 匹茲堡方法——在這種方法中，一個染色體編碼一個解，因此適應度分配給解。

• 密歇根方法——一個解通常由多個染色體表示，因此適應度分配給部分解。

需要注意的是，交叉、變異、拉馬克式或達爾文式等標準問題也存在於GBML系統中。