遺傳演算法 - 簡介

遺傳演算法 (GA) 是一種基於遺傳和自然選擇原理的基於搜尋的最佳化技術。它經常用於尋找難以解決的問題的最優解或近似最優解，否則這些問題需要花費一生才能解決。它經常用於解決最佳化問題、研究和機器學習。

最佳化簡介

最佳化是改進某些事物的過程。在任何過程中，我們都有一組輸入和一組輸出，如下圖所示。

最佳化是指以獲得“最佳”輸出值的方式查詢輸入值。 “最佳”的定義因問題而異，但在數學術語中，它指的是透過改變輸入引數來最大化或最小化一個或多個目標函式。

所有可能的解或輸入可以取的值的集合構成了搜尋空間。在這個搜尋空間中，存在一個點或一組點給出最優解。最佳化的目標是在搜尋空間中找到該點或點集。

什麼是遺傳演算法？

自然一直是全人類偉大的靈感源泉。遺傳演算法 (GA) 是基於自然選擇和遺傳概念的基於搜尋的演算法。GA 是一個更大的計算分支（稱為進化計算）的子集。

GA 由 John Holland 及其在密歇根大學的學生和同事（最著名的是 David E. Goldberg）開發，此後已在各種最佳化問題上進行了嘗試，並取得了高度成功。

在 GA 中，我們有一個給定問題的可能解的池或種群。然後，這些解會經歷重組和變異（就像在自然遺傳中一樣），產生新的子代，並且該過程在各個世代中重複。每個個體（或候選解）都被賦予一個適應度值（基於其目標函式值），並且適應性更強的個體有更高的交配機率併產生更多“適應性更強”的個體。這符合達爾文的“適者生存”理論。

這樣，我們就可以在幾代人的時間裡不斷“進化”出更好的個體或解決方案，直到達到停止標準。

遺傳演算法本質上是足夠隨機的，但它們比隨機區域性搜尋（我們只嘗試各種隨機解，跟蹤迄今為止最好的解）要好得多，因為它們也利用歷史資訊。

GA 的優勢

GA 具有多種優勢，使其廣受歡迎。這些包括：

• 不需要任何導數資訊（許多現實世界問題可能無法獲得）。

• 與傳統方法相比，速度更快，效率更高。

• 具有非常好的並行能力。

• 最佳化連續函式和離散函式以及多目標問題。

• 提供一系列“好的”解決方案，而不僅僅是一個解決方案。

• 總是得到問題的答案，隨著時間的推移會越來越好。

• 當搜尋空間非常大並且涉及大量引數時非常有用。

GA 的侷限性

與任何技術一樣，GA 也有一些侷限性。這些包括：

• GA 不適用於所有問題，特別是那些簡單且可以獲得導數資訊的問題。

• 適應度值被重複計算，這對於某些問題來說可能是計算量很大的。

• 由於具有隨機性，因此無法保證解決方案的最優性或質量。

• 如果實現不當，GA 可能無法收斂到最優解。

GA – 動機

遺傳演算法能夠“足夠快”地提供“足夠好”的解決方案。這使得遺傳演算法在解決最佳化問題方面具有吸引力。需要 GA 的原因如下：

解決難題

在計算機科學中，有一大類問題是NP-Hard 的。這實際上意味著，即使是最強大的計算系統也需要很長時間（甚至數年！）才能解決該問題。在這種情況下，GA 被證明是提供可用的近似最優解的有效工具，並且時間較短。

基於梯度的方法的失敗

傳統的基於微積分的方法的工作原理是從一個隨機點開始，並沿梯度的方向移動，直到我們到達山頂。這種技術效率很高，並且非常適用於單峰目標函式，例如線性迴歸中的成本函式。但是，在大多數現實世界的情況下，我們有一個非常複雜的問題，稱為景觀，它由許多山峰和許多山谷組成，這會導致此類方法失敗，因為它們具有固有的傾向於停留在區域性最優值，如下圖所示。

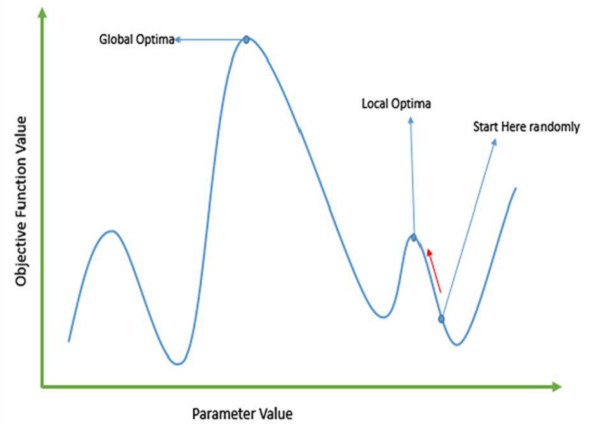
快速獲得良好的解決方案

旅行商問題 (TSP) 等一些難題具有現實世界的應用，例如路徑查詢和 VLSI 設計。現在假設您正在使用 GPS 導航系統，並且它需要幾分鐘（甚至幾小時）才能計算出從起點到目的地的“最佳”路徑。在現實世界的應用中，這種延遲是不可接受的，因此需要“足夠好”的解決方案，並且“快速”交付。