資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究定點數和浮點數表示
數字計算機使用二進位制數系統來表示計算機內部所有型別的資訊。字母數字字元使用二進位制位（即 0 和 1）表示。數字表示更容易設計，儲存方便，精度更高。
數字表示法有多種技術，例如：二進位制數系統、八進位制數系統、十進位制數系統和十六進位制數系統等。但是，二進位制數系統在數字計算機系統中表示數字最相關和流行。
儲存實數
這些結構如下所示：
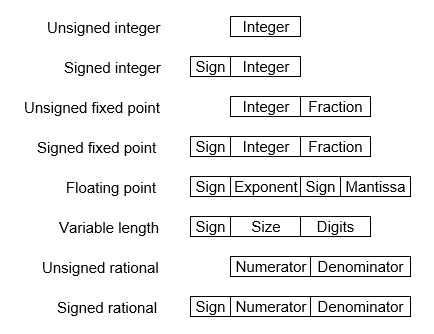
在現代計算中，有兩種主要方法可以儲存實數（即帶有小數部分的數字）。它們是 (i) 定點表示法和 (ii) 浮點表示法。在定點表示法中，小數點後有固定數量的數字，而浮點數允許小數點後有可變數量的數字。
定點表示法：
這種表示法為整數部分和小數部分保留固定數量的位。例如，如果給定的定點表示法是 IIII.FFFF，則可以儲存的最小值為 0000.0001，最大值為 9999.9999。定點數字表示法有三個部分：符號位、整數位和小數位。
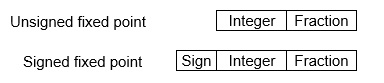
我們可以使用以下方法表示這些數字：
- 有符號表示：範圍從 -(2(k-1)-1) 到 (2(k-1)-1)，其中 k 為位數。
- 反碼錶示：範圍從 -(2(k-1)-1) 到 (2(k-1)-1)，其中 k 為位數。
- 補碼錶示：範圍從 -(2(k-1)) 到 (2(k-1)-1)，其中 k 為位數。
補碼表示法由於其明確的屬性以及更容易進行算術運算，因此在計算機系統中更受歡迎。
**示例：**假設數字使用 32 位格式，其中 1 位用於符號，15 位用於整數部分，16 位用於小數部分。
那麼，-43.625 表示如下：
其中，0 用於表示 +，1 用於表示 -。000000000101011 是十進位制 43 的 15 位二進位制值，1010000000000000 是小數 0.625 的 16 位二進位制值。
使用定點表示法的優點是效能，缺點是它們可以表示的值範圍相對有限。因此，它通常不足以進行數值分析，因為它不允許足夠的數字和精度。表示超過 32 位的數字必須不精確地儲存。
以上是如上格式所示的 32 位表示中可以儲存的最小正數和最大正數。因此，最小正數為 2-16 ≈ 0.000015（近似值），最大正數為 (215-1)+(1-2-16)=215(1-2-16) =32768，這些數字之間的差距為 2-16。
我們可以僅使用整數字段為 1 來向左或向右移動基數點。
浮點表示法：
這種表示法不會為整數部分或小數部分保留特定數量的位。相反，它為數字保留一定數量的位（稱為尾數或有效數），並保留一定數量的位來說明小數點位於該數字中的哪個位置（稱為指數）。
數字的浮點數表示有兩個部分：第一部分表示一個有符號定點數，稱為尾數。第二部分指定小數點（或二進位制點）的位置，稱為指數。定點尾數可以是小數或整數。浮點數始終解釋為以下形式表示的數字：Mxre。
只有尾數 m 和指數 e 在暫存器中物理表示（包括它們的符號）。浮點二進位制數以類似的方式表示，只是它使用以 2 為底的指數。如果尾數的最高有效位為 1，則浮點數被認為是規範化的。
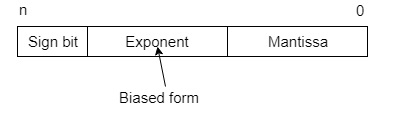
因此，實際數字為 (-1)s(1+m)x2(e-Bias)，其中 *s* 是符號位，*m* 是尾數，*e* 是指數值，*Bias* 是偏差數。
請注意，有符號整數和指數由符號表示、反碼錶示或補碼錶示表示。
浮點表示法更靈活。任何非零數都可以表示為 ±(1.b1b2b3 ...)2x2n 的規範化形式。這是數字 x 的規範化形式。
**示例：**假設數字使用 32 位格式：1 位符號位，8 位用於有符號指數，23 位用於小數部分。不儲存前導位 1（因為它對於規範化數字始終為 1），它被稱為“隱藏位”。
然後 -53.5 規範化為 -53.5=(-110101.1)2=(-1.101011)x25，表示如下：
其中 00000101 是指數值 +5 的 8 位二進位制值。
請注意，8 位指數字段用於儲存整數指數 -126 ≤ n ≤ 127。
適合 32 位的最小規範化正數為 (1.00000000000000000000000)2x2-126=2-126≈1.18x10-38，適合 32 位的最大規範化正數為 (1.11111111111111111111111)2x2127=(224-1)x2104 ≈ 3.40x1038。這些數字表示如下：
浮點格式的精度是為二進位制數字保留的位置數加一（對於隱藏位）。在此處考慮的示例中，精度為 23+1=24。
1 和下一個規範化浮點數之間的差距稱為機器 epsilon。對於上述示例，差距為 (1+2-23)-1=2-23，但由於非均勻間距，這與最小正浮點數相同，這與定點情況不同。
請注意，非終止二進位制數可以用浮點表示法表示，例如，1/3 = (0.010101 ...)2 不能是浮點數，因為它的二進位制表示是非終止的。
IEEE 浮點數表示法：
IEEE（電氣和電子工程師協會）已將浮點表示法標準化為下圖所示。
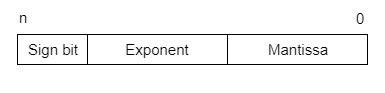
因此，實際數字為 (-1)s(1+m)x2(e-Bias)，其中 *s* 是符號位，*m* 是尾數，*e* 是指數值，*Bias* 是偏差數。符號位對於正數為 0，對於負數為 1。指數由補碼錶示。
根據 IEEE 754 標準，浮點數以以下方式表示：
- 半精度 (16 位)：1 個符號位、5 位指數和 10 位尾數
- 單精度 (32 位)：1 個符號位、8 位指數和 23 位尾數
- 雙精度 (64 位)：1 個符號位、11 位指數和 52 位尾數
- 四精度 (128 位)：1 個符號位、15 位指數和 112 位尾數
特殊值表示：
根據 IEEE 754 標準，存在一些取決於指數和尾數的不同值的特殊值。
- 所有指數位為 0，所有尾數位為 0 表示 0。如果符號位為 0，則為 +0，否則為 -0。
- 所有指數位為 1，所有尾數位為 0 表示無窮大。如果符號位為 0，則為 +∞，否則為 -∞。
- 所有指數位為 0 且尾數位非零表示非規格化數。
- 所有指數位為1且尾數位非零表示錯誤。
瀏覽量：9.8萬+
